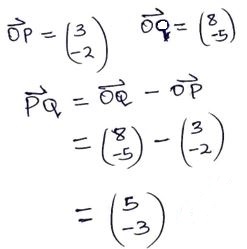Questions
INSTRUCTIONS TO THE CANDIDATES
- This paper consists of two sections; Section I and Section II.
- Answer All questions in Section I and only Five questions from section II
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations giving answers at each stage in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- Candidates should answer questions in English.
SECTION I (50 MARKS)
Answer ALL the questions in this section in the spaces provided
- Use logarithm tables to evaluate ∛(45.3×0.00697/0.534) (4mks)
- Express
as a fraction. (3mks)
- Simplify √5/√7-√2 (3mks)
- The lengths of wires were 30 m, 36 m and 84 m. Pieces of wire of equal length were cut from the three wires. Calculate the least number of pieces obtained. (4mks)
- The size of an interior angle of regular polygon is 3xo. While its exterior angle is (x – 20)o. Find the number of sides of the polygon. (3mks)
- Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm. (answer to 2 d.p.) (3mks)
- A man wishes to save sh. 200 000 in 4 years time. Find, to the nearest shilling, the sum of money he has to deposit now at 12% p.a. interest, compounded semi-annually to realize his goal. (3mks)
- Use completing the square method to solve 2x^2+4x+1=0 . Write your answer correct to 4 d.p. (3mks)
- Solve for x in: (log2x)2+log28 - log2x4 =0 (4mks)
- Determine the equation of a line that passes through (-2,5) and is parallel to the line whose equation is 〖5y+2x=10〗_( ) (4mks)
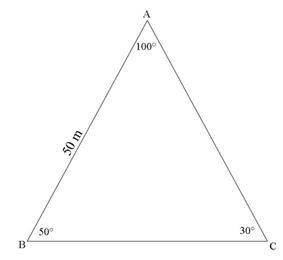
- In the figure below, if a circle is drawn passing through A, B and C what would be the radius of the circle (4mks)
- Given that Sin(x+ 20o) = cos(2x+25) find the value of x and hence find the value of tan x. (2mks)
- An arc of a circle of radius 4 cm is 5 cm long. Calculate the angle subtended by the arc at the center in radians (2mks)
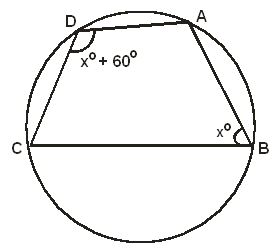
- The figure below shows a quadrilateral ABCD which is cyclic. Solve for x. (2mks)
- Simplify log25+log625 /log5 (3mks)
- Given that OP = 3i – 2j and OQ = 8i – 5j. Find |PQ| to 3 significant figures. (3mks)
SECTION II: (50 MARKS)
Answer only FIVE questions from this section in the spaces provided
-
- Mr. Kobe is a civil servant who earns a monthly salary of Ksh.21200. He has a house allowance of Ksh.12000 per month, other taxable allowances are commuter Ksh.1100, medical allowance Ksh.2000. He is entitled to a personal relief of Ksh.1240 per month.
Using the income rates below, solve the questions that follow.
Determine;Income in Ksh. per month Rates in Ksh per sh 20 1 – 8,400
8401 – 18,000
18001 – 30,000
30001 – 36,000
36001 – 48,000
Above 48,0002
3
4
5
6
7- His monthly taxable income. (2mks)
- Net tax (PAYEE) (5mks)
- In addition to the PAYEE, the following deductions were made. Ksh.250 for NHIF, Ksh.120 service charges, he repays a loan at sh.4500 and contributes towards savings at sh.1800 every month. Calculate his net salary per month. (3mks)
- Mr. Kobe is a civil servant who earns a monthly salary of Ksh.21200. He has a house allowance of Ksh.12000 per month, other taxable allowances are commuter Ksh.1100, medical allowance Ksh.2000. He is entitled to a personal relief of Ksh.1240 per month.
- Mr. Korir borrowed Khs 3,600,000 from the bank to buy a residential house. He was required to repay the loan with a simple interest for a period of four years. The repayment amounted to kshs 111 000 per month. Calculate;
- The interest paid to the bank. (1mk)
- The rate per annum of the simple interest. (2mks)
- The value of the house appreciated at the rate of 15% per annum. Calculate the value of the house after 4 years to the nearest hundreds. (3mks)
- After n years, the value of the house was Kshs 8,327,019. Find the value of n. (4mks)
-
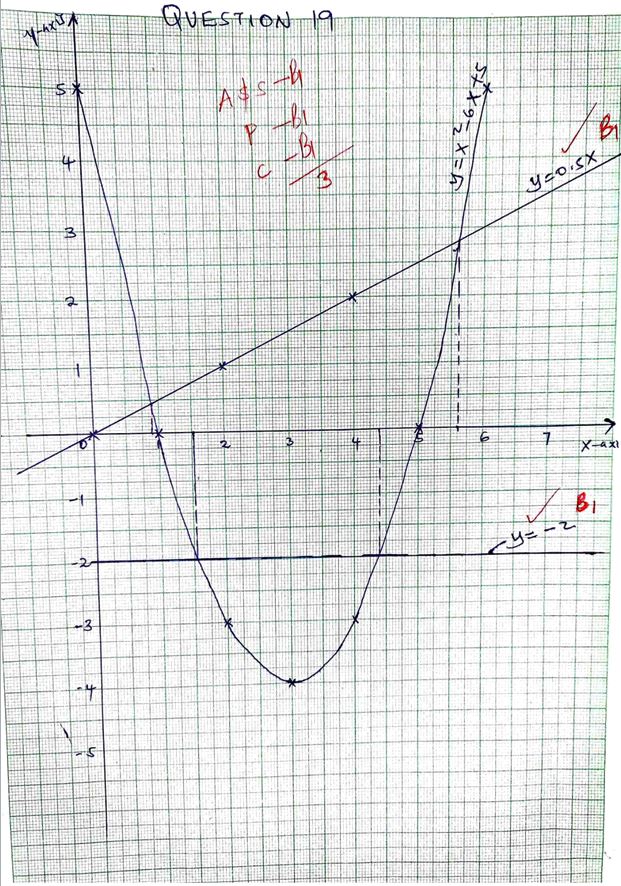
- Complete the table below for the equation y=x2-6x+5 (2mks)
X 0 1 2 3 4 5 6 X2 0 4 9 25 -6x 0 -6 -24 -36 5 5 5 5 5 5 5 5 y 5 - Draw the graph of y=x2 – 6x + 5 using the values in the table. (3mks)
- Use the graph to solve the equations
- x2 - 6x + 5 = 0 (1mk)
- x2 – 6x + 7 = 0 (2mks)
- x2 – 6.5x + 5 = 0 (2mks)
- Complete the table below for the equation y=x2-6x+5 (2mks)
-
- A matatu travelling at 99km/h passes a checkpoint at 9.00 am. A police patrol car travelling at 132km/h in the same direction passes through the police check point at 9.15 a.m. If the matatu and the police patrol car continue at their uniform speeds, calculate:
- the relative speed of the two vehicles (1mk)
- the distance between the two vehicles as at 9.15 a.m. (2mks)
- the time the police car will overtake the matatu. (3mks)
- Two passenger trains A and B which are 240m apart and travelling at 164km/h and 88km/h respectively approach one another on a straight railway line. Train A is 150m long and train B is 100m long. Determine the time in seconds that elapses before the two trains completely pass each other. (4mks)
- A matatu travelling at 99km/h passes a checkpoint at 9.00 am. A police patrol car travelling at 132km/h in the same direction passes through the police check point at 9.15 a.m. If the matatu and the police patrol car continue at their uniform speeds, calculate:
- The marks scored in a form three Maths exam were recorded as follows
69
63
62
35
5370
54
64
34
5772
57
58
58
5640
48
39
64
7252
47
45
62
5660
56
48
37
4822
55
65
41
4431
62
50
42
5578
75
85
36
7853
38
46
54
5928
37
47
82
5067
44
57
48
45- Starting with a class of 20 – 29, make a frequency distribution table for the above data (2mk)
- What is the modal class of the test (1mk)
- Calculate the mean of the data (4mk)
- Calculate the median mark to 1 d.p. (3mk)
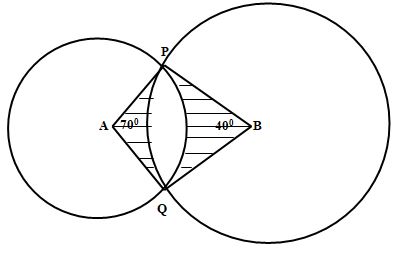
- The diagram below shows two circles, centre A and B which intersect at points P and Q.
Angle PAQ = 700, angle PBQ = 400 and PA = AQ = 8cm.
Calculate- PQ to correct to 2 decimal places (2mks)
- PB to correct to 2 decimal places (2mks)
- Area of the minor segment of the circle whose centre is A to 2 decimal places (2mks)
- Area of shaded region (4mks)
-
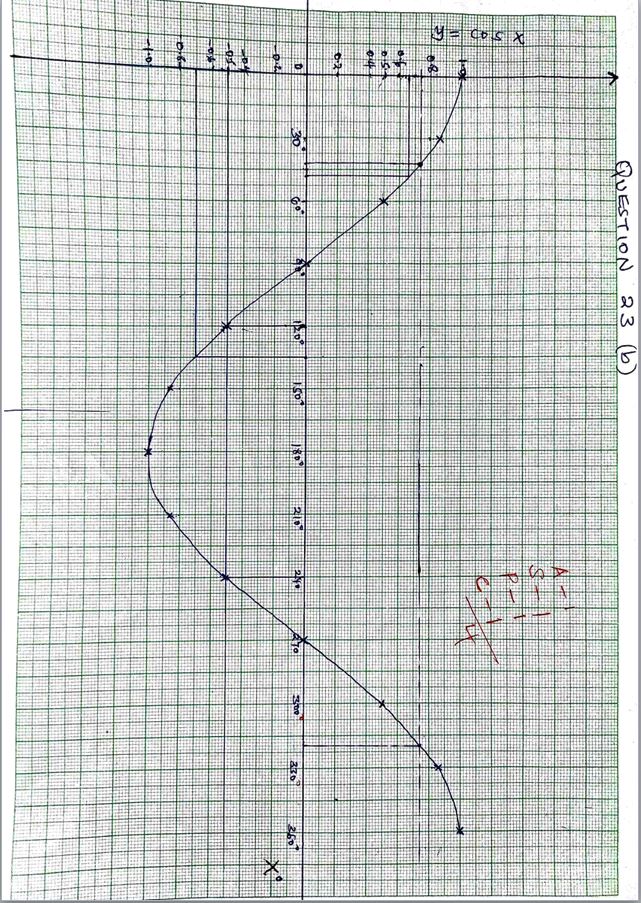
- Complete the table below for y=cosx for 0°≤x≤360° (2mks)
X° 0 30 60 90 120 150 180 210 240 270 300 330 360 y=cos x - Draw the graph of y=cosx . (4mks)
- Use the graph in (b) above to to solve for the values of x in the following (2mks)
- cosx=0.74
- cos x = - 0.5
- Use the graph in (b) above to find the cosine values of the following angles;(2mks)
- 48°
- 135°
- Complete the table below for y=cosx for 0°≤x≤360° (2mks)
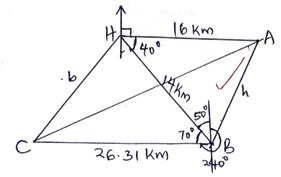
- Three ships A, B, and C are approaching a harbor H. Ship A is 16 km from the harbor on a bearing of 0900. Ship B is 14 km from the harbor on a bearing of 1300, and ship C is 26.31 km to the west of B and on a bearing of 2400 from the harbor. Without using scale drawing, calculate, to 2 decimal places, the distance:
- between A and B (3mks)
- of ship C from the harbor (3mks)
- between A and C (4mks)
Marking Scheme
-
1. + 0.92393No Std Form Log 45.3
0.00697
0.5344.53 x 101
6.97 x 10-3
5.34 x 10-11.6561
3.8432
1.4993
1.7275
1.7718 ÷ 3
1.9239
8.392 x 10-2
=0.8392 - 1r = 0.407407
1000r= 704.407407
999r= 407
r= 407
999 - √5
√7 -√2
√5 (√7 + √2)
(√7 - √2) (√7 + √2)
√35 + √10
√49 + √14 - √14 - √4
√35 + √10
7- 2
√35 + √10
5 - GCD required
2 x 3 = 62 30 36 84 3 15 18 42 5 6 14
Least number of pieces
comparing the three:
30/6 = 5 pieces
36/6 = 6 pieces
84/6 = 14 pieces
5 pieces is the least - 3x° + (x - 20°) = 180°
4x° - 20° = 180
4x° = 200°
x° = 50°Size of exterior angle
= 50° - 20° = 30°
no of sides = 360/30
=12 sides - V = 8.2 x 6.2 x 5.7
individual absolute errors
0.1/2 0.1/2 0.1/2
0.05 0.05 0.05
RE in volume = Sum of individual REs
0.05 + 0.05 + 0.05
8.2 6.2 5.7
=0.0229
%age error = 0.0229 x 100 = 2.29% - Rate= 1/2 x 12 = 6%
Compound interest AP(1 + r/100)n
200 000= P(1 + 6/100)8
200 000 = 1.068
P = 200 000
1.068
= sh. 125 482 -
2x2 + 4x + 1 = 0
2 2 2 2
x2 + 2x + 1/2 = 0
x2 + 2x = -1/2
x2 + 2x + (2/2)2 = 1/2 + (2/2)2
(x + 1)2 = 1/2
x + 1 = ±√0.5
x = -0.2929 or x = -1.707 - (Log2θ)2 + 3Log22 - 4Log2θ = 0
Let Log2θ= x
x2 + 3 - 4x = 0
x2 - 4x + 3 = 0
x2 - 3x - x + 3=0
x(x-3)-1(x-3)= 0
(x-1)(x-3)=0
x=1 or x =3
but
Log2θ = x
Log2θ = 1
θ = 21=2
also log2θ=3
θ=23
θ=8 - For parallel lines
m1=m2
5y= -2x + 10
y= -2/5x + 2
m1 = -2/5
m2 = -2/5
P(-2,5)
y-5 = -2
x+2 5
5(y-5) = -2(x+2)
5y - 25 = -2x -4
5y = -2x + 21
y= -2/5x + 21/5 - a = b = c = 2r
Sin A Sin B Sin C
c/Sin C = 2r
50/Sin 30 = 2r
100 = 2r
r=50m - Complementary angles
(x + 20°)+(2x + 25)° = 90°
3x + 45° = 90°
3x=45°
x=15°
tan x = tan 15°
= 0.2679 - 1c = 4cm
? = 5cm
5 x 1 - x° + 60° + x° = 180°
2x° + 60 = 180°
2x° = 120°
x=60° - log 5 ² + log 5⁴
Log 5
2 Log 5 + 4 Log 5
Log 5
(2+4)Log 5
log 5
= 6 -
⇀
| PQ | = √(52 + (-3)2
=√34 = 5.83 -
-
- 21 200 + 12 000 + 1 100 + 2 000
= 36 300
8400 x 2
20
9600 x 3
20
12000 x 4
20
6000 x 5
20
300 x 6
20840
+
1440
+
2400
+
1500
+
90
6 270
Net tax - Gross - relief :
6 270 - 1 240 = 5 030
- 21 200 + 12 000 + 1 100 + 2 000
- Net salary = 36 300 - (5030 + 250 + 120 + 4500 + 1800)
+ 36 300 - 11 700 = 24 600
-
-
- I = (111000 x 12 x 4) - 3 600 000= 1 728 000
- 1 728 000 = 3 600 000 x r/100 x 4
r = 1 728 000 x 100
3 600 000 x 4
= 12% - A= 3 600 000 (1 + 15/100)4
3 600 000 (1.15)4
6 296 422.5
6 296 400 - 8 327 019 = 3 600 000 (1 + 15/100)n
2.313 = (1.15)n
Log 2.313 = Log 1.15n
Log 2.313 = n Log 1.15
n = Log 2.313 = 5.9998
Log 1.15
= 6 years
- I = (111000 x 12 x 4) - 3 600 000= 1 728 000
-
-
X 0 1 2 3 4 5 6 X2 0 1 4 9 16 25 36 -6x 0 -6 -12 -18 -24 -30 -36 5 5 5 5 5 5 5 5 y 5 0 -3 -4 -3 0 5 -
-
- y = x² - 6x + 5
-0 = x² - 6x + 5
y= 0 ,
x=1 or x=5 - y = x² - 6x + 5
-0= x² - 6x + 7
y = -2,
x = 1.55 or x = 4.4 - y = x² - 6x + 5
-0 = x² - 6.5x + 5
y= 0.5x
x= 0.9 or x = 5.6
x 0 2 4 y 0 1 2
- y = x² - 6x + 5
-
-
-
- 132 - 99 = 33km/hr
- 15/60 x 99 = 24.75km
- time = distance/speed
= 24.75/33
45 min
9:15
+45
10.00am
- Relative/ total distance
240 + 150 + 100 = 490m = 0.49km
Rel speed
164km/h + 88km/h = 252km/h-1
T = 0.49 = 0,00194 = 7 seconds
252
-
-
-
Class Midpoint X f fx cf 20 - 29
30 - 39
40 - 49
50 - 59
60 - 69
70 - 79
80 - 8924.5
34.5
44.5
54.5
64.5
74.5
84.52
8
14
18
10
6
249
276
623
981
645
447
1692
10
24
42
52
58
60Σf = 60 Σfx= 3190 - 50 - 59
- mean = Σfx/Σf
= 3190 = 53.2
60 - 49.5 + (12/18)10
= 56.167
= 56.2
-
-
- Sin 35° = NQ/8
NQ = 8 Sin 35°
= 4.5886 cm
PQ = 2 x 4.5886 = 9.1772 = 9.18cm - Sin 20° = 4.59/PB
PB = 4.59
Sin 20 °
PB = 13.42cm - 70/360 x 22/7 x 82 - 1/2 x 82 x Sin 70°
= 39.1111 - 30.07
= 9.04cm2 - Segmented area
40/360 x 13.42 x 13.42 x 22/7 - 1/2 x 13.42 x 13.42 x Sin 40°
62.89 - 57.88
= 5.01
Area of shaded
= [(30.07 + 57.88) - (9.04 + 5.01)]
87.95 - 14.05 = 73.9cm2
- Sin 35° = NQ/8
-
-
X° 0 30 60 90 120 150 180 210 240 270 300 330 360 y=cos x 1.0 0.87 0.5 0.0 +0.5 -0.87 -1.0 -0.87 -0.5 0 0.5 0.87 1.0 -
-
- X = 42° ± 3, 319.5° ± 3
- X= 120° , 240°
-
- Cos 48° = 0.66
- Cos 135° = -0.7
-
-
-
AB = h
h² = 14² + 16² - 2 x 14 x 16 Cos 40°
= 452 - 343.188
= 108.812
h = √108.812 = 10.43km - Angle at B = 360° - (240° + 50°) = 70°
CH = b
b² = 14² + 26.31² - 2 x 14 x 26.31 Cos 70°
= 888.2161 - 251.96
= 636.257 - Angle at B
h = 16
Sin H Sin B
10.43 = 16
Sin 40° Sin B
Sin B = 16 Sin 40°
10.43
= 0.9861
B = Sin-1 0.9861
B = 80.4°
<CBA = 70° + 80.4° = 150.4°
AC² = 26.31² + 10.43² - 2 x 26.31 x 10.43 Cos A
=801.001 -(-477.20)
1278.203
AC = √1278.203
35.75km
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Questions and Answers - Form 3 Term 2 Opener Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students