Mathematics Questions and Answers - Form 3 Mid Term 1 Exams 2023

• This paper consists of two sections: Section I and Section II.
• Answer all questions in section I and Section II.
• Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
• Marks may be given for correct working even if the answer is wrong.

SECTION I (50 Marks)      
Answer all the questions in this section

1. Evaluate  (−4 of (−4 + −5÷15)+ −3−4÷2)                 (3 marks)
                               (84÷-7+3− −5)
2. Muya had 6 ²/₃ hectares piece of land. He donated ⁷/₈ hectare to a school and 1½ hectare to a children home .The rest of the land was shared equally between the son and the daughter. Find the size of the land that each child got.                                                         (3 marks)
3. Without using mathematical table or calculate evaluate    1.9 ×0.032                    (3 marks)
                                                                                              20 × 0.0038
4. The shopping centres Miseleni and Katheka are 17 km apart. Kioko walks towards Miseleni at an average speed of 9 km/h. Forty-five minutes later Cherono cycles from Katheka towards Miseleni at an average speed of 30 km/h. Calculate the distance from Miseleni when Cherono catches up with Kioko.                                                (4 marks)
5. Use logarithm tables to evaluate                                                                           (4 marks)
   1721² × √0.024
             321
6. Solve for the value of x which satisfy the equation;                                          (3 marks)
   32^{x − 3}  × 8^x+4 = 64 × 2^x
7. Moraa spends a total of Ksh. 970 on buying 3 text books and 5 pens. If she had bought 2 textbooks and 8 pens, she would have saved Ksh. 90. Find the cost of one text book.                         (3 marks)
8. A piece of wire is to be divided into 20cm or 24cm or 28cm for construction and leave        15 cm piece .Find the shortest length of the  wire          (3 marks)
9. Given that 3x is an acute angle and sin 3x = cos 2x find the value of x.        (3 marks)
10. A retailer buys 30 boxes of strawberries at sh. 30 each and sells 27 boxes at 30% profit. How much profit does he make?         (3 marks)
11. Factorize then simplify           (3 marks)
    2bx − 2by + 3ax − 3ay
               3a+2b
12. The base of an open rectangular tank is 3.2m, by 2.8 m .Its height is 2.4m .It contains water to a depth of 1.8m. Calculate the surface area inside the tank that is not in contact with water.                     (3 marks)
13. An empty 300 ml bottle has a mass of 270g. Calculate the mass of the bottle when it is full of a liquid whose density is 1.1gcm^-3     (3 marks)
14. Evaluate the expression below using reciprocal tables and give your answer to two decimal places.   (3 marks)
      6    +      2    
    321       0.042
15. By factor method find the cube root of the following;
    1. ∛8                                                                                                                  (1 mark)
    2. ∛64                                                                                                                (2 marks)
16. Simplify the expression                                                                                       (3 marks)
    2x² + 3x − 2
        x² − 4

SECTION II (50 Marks)     
Answer all the questions in the spaces provided

17. The height in centimeters of 18 form one students are shown below 
    

    132	132	156	147	162	168
    174	141	136	161	148	152
    140	174	162	143	154	174

    1. Using a class width of 10 and starting with a class of 130 – 139 as the first class make a frequency distribution table             (2 marks)
    2. State the modal class                                                                                               (1 mark)
    3. Modify the above table and calculate
       1. Mean height                                                                                    (4 marks)
       2. Median height                                                                                 (3 marks)
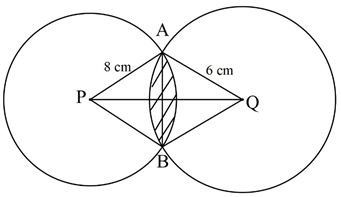
18. The figure below shows two circle of radii 8cm and 6cm with center P and Q respectively. 
    
    The circles intersect at point A and B. The lines PQ and AB are perpendicular to each other and meet at X. If the common chord AB is 9 cm, calculate
    1. ∠AQB                                                                                                         (2 marks)
    2. ∠APB                                                                                                         (2 marks)
    3. Area of segment whose centre is P                                                             (2 marks)
    4. Area of segment whose centre is Q                                                            (2 marks)
    5. Area of the region between the intersecting circles                                    (2 marks)
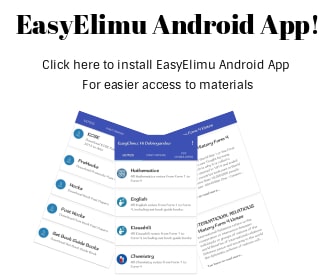
19. A kite has vertices A(1,1),B(6,2),C(6,6) and D(2,6).
    1. Draw the kite ABCD.                                                                                  (1 mark)
    2. On the same axes draw,
       1. A'B'C'D' the image of ABCD under a rotation of a positive quarter turn about  the origin. State its coordinates.                           (3 marks)
       2. A'' B''C''D'' the image of A'B'C'D' under a reflection in the line y−x=0. State its coordinates.                                                  (3 marks)
       3. A'''B'''C'''D'''  the image of A''B''C''D'' under enlargement of scale factor −0.5 about the origin. State its coordinates.               (3 marks)
20.  
    1. A line L passes through the points A(−2,3) and B(−1,6)
       1. Find the gradient  of the line L                                                                   (1 mark)
       2. Find the equation of the line L in the form y=mx+c                           (2 marks)
    2. A second line P is perpendicular to line L at point (−1,6) .Find the equation of line P in the form  ax + by=c                          (2 marks)
    3. Given that a third line Q is parallel to line L and passes through point (1,2). Find the equation of lines Q in the form ax+by = c     (2 marks)
    4. Find the point of intersection of lines P and Q                                               (3 marks)
21. On the graph provided draw the region that satisfies the following linear inequalities.                         (10 marks)
    2x − y≥ −4
    x+y≤4
    y≥0
    x<3

MARKING SCHEME

No	Working	Remarks
1	N⟹−4×(−4+ −1/3)+ −3−2 =171/3 − 5 =121/3 D⟹84 ÷ −7 + 3 + 5 = −4 N/D⟹37/3× −1/4 = −31/12	M1  M1   A1
2	Land donated = 7/8 + 3/ = 19/8 Land shared = 20/3 − 19/8 = 103/24 Land each child gets = ½ × 103/24 = 27/48 hectares	M1  M1   A!
3	1.9 × 0.032 × 104    20 × 0.0038 × 104 =  19×32      20×38 = 4/5	M1  M1  A1
4	Distance between the two at the same time = 9 × 0.75 = 6.75 km Relative speed = 30 − 9 = 21km/hr Time taken = 6.75 = 0.321 hrs                        21 Distance = 6.75 × 30 = 9.64 km                     21 Distance from Miseleni =17− 9.64 = 7.36 km	M1    M1  M1  A1
5	No  Std Form   Log   17212   1.721 × 103  3.2357 × 2  6.4714  √0.024  2.4 × 10−2    N       5.6615  321  321 ×102   2.5065−   1429  103 × 100.1550   3.1550	B1 – all correct logs B1 – addition and subtraction B1 – square root B1 – final correct answer
6	25(x-3) × 23x+12 = 26+x 25x −15 + 3x+12 = 26+x 5x − 15 + 3x +12 = 6 + x  7x = 9  x = 1 2/7	M1  M1  A1
7	3b + 5p = 970 ....... (i) 2b + 8p = 880 ....... (ii) From (i) b = 970 − 5p                         3 Thus 2 (970 − 5) + 8p = 880                   3 2(970 − 5p) + 24p = 2640 14p = 700      p = 50 b = 970 − 250 = 240             3 Cost of a book = Sh. 240	B1 – both equations  M1  A1
8	20 = 22 × 5 24 = 23 × 3 28 = 22 × 7 LCM of 20, 24 & 28 = 23 × 3 × 5 × 7 = 840 Length of the wire = 840 + 15 = 815 cm	B1  M1  A1
9	For complementary angles, A + B = 90° 3x + 2x = 90° 5x = 90°  x = 18°	B1  M1  A1
10	Buying price = 30 × 30 = Sh.900 Selling price = 27 × 1.3 × 30 = Sh.1053 Profit =1053 − 900 = Sh.153	M1 – both B.P & S.P M1 A1
11	2b(x − y) +3a(x − y)         3a+2b = (3a+2b)(x − y)        (3a+2b) = x − y	M1  M1  A1
12	Total surface area = (0.6×2.8×2) + (3.2×0.6×2)                               = 3.36+3.84                                = 7.2 m2	M1  M1  A1
13	Mass = 300 × 1.1=330 g Total mass = 270 + 330 = 600g ≅ 0.6kg	M1  M1 A1
14	1   = 3.115× 10-3 321    1     = 2.38 × 101 0.042 (6 × 3.115 × 10-3) + (2 × 2.381 × 101) 0.01869 + 47.62 ≅ 47.64 (2 d.p)	M1 - both values  M1  A1
15	8  = 23 ∛8 = 23×1/3 = 2 64 = 26 ∛64 = 26×1/3 = 2 × 2 = 4	B1  M1  A1
16	2x2 + 3x − 2 ⟹ (2x−1) (x+2) x2 − 4 ⟹ (x − 2)(x + 2) 2x2 + 3x − 2 = (2x−1)(x+2)      x2 − 4          (x−2)(x+2)  = 2x − 1     x − 2	M1  M1  A1
17	Class  130-139  140-149  150-159   160-169   170-179   Frequency       3        5         3        4       3  140 - 149      Class  Frequency, f   fx   130-139   3   403.5   140-149   5   722.5  150-159    3   463.5   160-169    4   658  170-179   3  523.5   Totals  18   2771  Mean = ∑fx  = 2771                ∑f        18                                                                         =153.94 cm   Median = L + (N/2 − c.f)) × i                             f              = 149.5+ (9 − 8) ×10                                  3              = 149.5 + 3.3 = 152.8 cm	B2 - correct table  B1 - modal class  B2 - f & fx column     M1   A1   M1M1      A1
18	Let angle AQX be θ sin⁡ θ = 4.5                6 θ=sin-1(4.5/6) = 48.59 Angle AQB = 2 × 48.59° = 97.18° Let angle APX be α sin⁡ α = 4.5               8 α = sin-1(4.5/8) = 34.23° Angle AQB = 2 × 34.23° = 68.46°   Area A1 = (68.46 × 22 × 64) − (½ × 64 × sin⁡ 68.46 )                    360       7 =37.13 − 29.77 =7.36 cm2   Area A2 = (97.18 × 22 × 36) − (½ × 36 × sin ⁡97.18 )                    360      7 = 30.54 − 17.86 =12.68 cm2   Total area = 7.3 + 12.68  =20.04 cm2	M1  A1   M1  A1  M1  A1  M1   A1  M1A1
19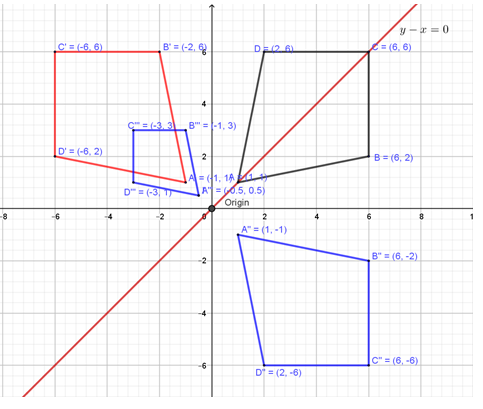
20	m =  6 − 3   = 3        −1−(−2)   y−3 = 3    x+2  y − 3 = 3x + 6  y = 3x + 9 m2 = −1/3 y−6 = −1/3 x+1 3y − 18 = −x−1 x + 3y = 17 m3 = 3  y − 2 = 3 x − 1 y − 2 = 3x − 3 y = 3x − 1 x + 3(3x − 1) = 17 x + 9x  − 3 = 17 10x=20     x=2 y=3(2) − 1 = 5 Point of intersection = X(2,5)	B1  M1  A1  M1  A1  M1  A1  M1  M1  A1
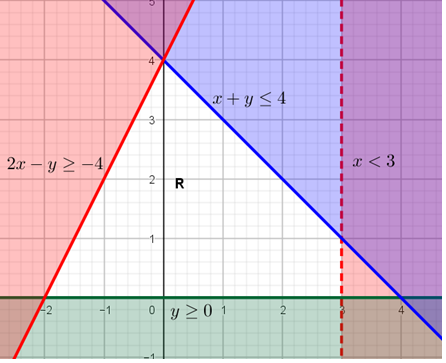
21	2x − y ≥ −4 x + y ≤ 4  y ≥ 0  x < 3	B3 – Table, line & shading  B3 - Table, line & shading B2 – line & shading B2 – line & shading