MATHEMATICS Paper 2 Questions and Answers - Form 3 End Term 1 Exams 2023

QUESTIONS

Evaluate without using tables or calculators. (3mks)
√^{0.8064 X 6.048}/_{1.008 X 0.1344}
Evaluate ^{-4 of [(-4 + -5 ÷15) + -3 - 4 ÷ 6)]}/_84÷-7+3--5 (2mks)
Solve for θ without using table given that 0 ≤ θ ≤ 90^o and that sin ( 2θ - 30^o) –cos4θ =0 (3mks)
Solve for x given that 5^{2x+ 2}– 20 X 5^2x=625 (3mks)
The angle of a quadrilateral ABCD in order are 2(x -10),4(x + 5),5(x+4) and (x-20) in degrees. Find the exterior angles of the quadrilateral. (4mks)
A radio costing kshs. 1240 is marked to sell at a price calculated to give a profit of 40 %. What will be its selling price in sale when 25% is taken off the marked price? (3mks)
Show that if OA = - i+ 7j, OB = 3i – 5j and OC = 4j, then points AB and C are collinear. (4mks)
Four men can dig 2 acres of land in 3 days working 4 hour a day. How many men are required to dig 5 acres of land in 4 days working 3 hours a day at the same rate. (3mks)
The surface area of two similar bottles are 12cm² and 108cm² respectively. If the larger one has a volume of 810cm³. Find the volume of the smaller one. (3mks)
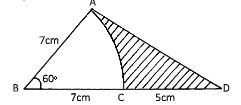
In the figure given below, AC is an arc of a circle centre B ABD = 60 o , AB = BC = 7cm and CD= 5 cm.

Calculate
1. The area of triangle ADB (2mks)
2. The area of the shaded region. (2mks)
Solve the inequalitites and represent the information on the number line. (3mks)
-3+2x<3x+2<4(x-5)
Make x the subject of the formula in 3s=2p√^X/_3X-5 (3mks)
Given x = 13.4cm and y = 4.3 cm. calculate the percentage error in ^x/_Y correct to 4 d.p( 3mks)
A straight line through the point A (2, 1) and B (4,m) is perpendicular to the line whose equation is 3y = 5 – 2x, Determine the value of m. (3mks)
Okoth deposited some money at 10% compound interest compounded annually. How long will it take to double the amount to the nearest year? (3mks)
Chebet has 5 brown chicken and 3 black ones. She picks two of them for slaughter at random, one after the other. What is the probability that the two are of different colours. (3mks)

SECTION II

Answer only five questions.

A bus left Nairobi at 8.00am and traveled towards BUsia at an average speed of 80km/hr. At 8.30 am a car left Busia for Nairobi at an average speed of 120km/hr. Given that the distance between Nairobi and Busia is 400km.Calculate:
1. The time the car arrived in Nairobi. (2mks)
2. The time the two vehicles met. (4mks)
3. The distance from Nairobi to the meeting point. (2mks)
4. The distance of the bus from Busia when the car arrived in Nairobi. (2mks)
A triangle whose vertices are A (1,4) B ( 2,1) and C (5,2) is given the following transformation:
1. Reflection in the line y = -x to A 1 B 1 C 1
2. A¹ B¹ C¹ is then given rotation of + 90 o about the origin to A¹¹ B ¹¹ C ¹¹
3. A¹¹ B¹¹ C¹¹ is then given a translation vector to A¹¹ B¹¹ C¹¹
4. A ¹¹ B ¹¹ C ¹¹ is then given an enlargement scale factor – 2 centre (0, 0) to A^IV B^IV C^IV .
  On the given grid plot a triangle ABC and it’s images A¹ B¹ C ¹ , A ¹¹ B ¹¹ C ¹¹ , A ¹¹¹ B ¹¹¹ C ¹¹¹ and A ^IV B ^IV C ^IV . And give coordinates of A ^IV B^IV C^IV . (10mks)
A Post OT stand vertically on level ground John moves from O, the foot of the flag post to point R, on the level ground. The points T, O and R from a right angled isosceles triangle whose perimeter is 56m. S is another point on the level ground 35m from O calculate:
1. The angle of elevation of T from S. (6mks)
2. The distance ST. (2mks)
3. Find the maximum possible distance between R and S. (2mks)
A salesman received a basic salary of sh. 50,000 a year together with a commission of 6 % on the value of goods sold and a car allowance of sh. 2.50 per km.
1. Find the total amount he received in a year in which he sells goods worth sh. 625,000 and travels 10,000km. (4mks)
2. The next year he travels 12,000km and receives a total of shs. 134,000
  1. Calculate the value of goods sold. (4mks)
  2. Calculate the percentage increase in the value of the goods sold. (2mks)
Two airports a and B are such that B is 500km due east of A. two plane P and Q take off from A and B respectively and at the same time.
Plane P files at 360km/hr on a bearing of 030^o
Plane Q flies at 240km/hr on a bearing of 315^o
The two planes land after 90 minutes.
Using a scale of 1: 10,000,000
1. Show the positions of the planes after 90 min. (6mks)
2. Find the distance between the planes after 90 min. (2mks)
3. Find the bearing of plane Q from plane P after 90 minutes (2mks)
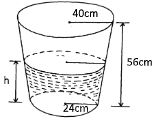
The figure below shows a container in form a frustrum of an open top radius 40cm and base radiu24cm. the depth is 56 cm. 56cm
1. Calculate the volume of the container in litres. (4mks)
2. Of the container is ¾ full of water by volume,
  Calculate the radius of the meniscus. (6mks)
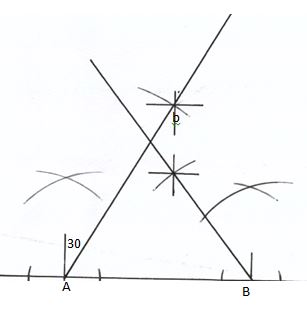
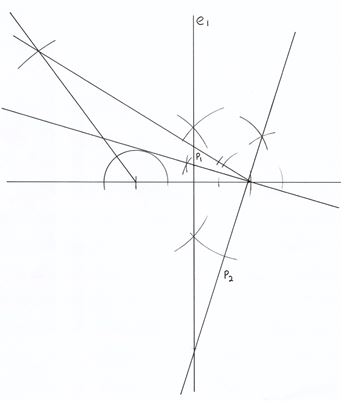
Use a ruler and compass only in this question.
1. Construct ∆ ABC such that AB = 6cm AC= 8.5 cm and < BAC = 120^o (3mks)
2. Construct the locus ℓ, of points equidistant from A and B (2mks)
3. Construct the locus ℓzof points equidistant from AB and BC (3mks)
4. Find the points of intersection, P₁ and P₂ , of 1₁ and 1₂ and measure P₁ P₂ (2mks)
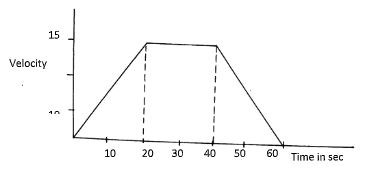
The diagram below shows the graph of a moving matatu from one bus stop to another.
1. Find the acceleration of the matatu. (2mks)
2. Find the deceleration of the matatu (2mks)
3. Calculate the distance the matatu while accelerating. (2mks)
4. Calculate the distance the matatu covered while traveling at an acceleration of 0m/s 2 (2mks)
5. Find the distance between the two bus stops.

MARKING SCHEME

√^{0.8064 x 1000}/_{1.008 x 10000} x ^{6.048 x 10000}/_{0.134 x 1000}^√80.64/ ₄₀₀₈ x ⁶⁰⁴⁸/₁₃₄₄
4 x 9 = 36
-4 (-4 ⅓ )
- 12 3 5
^{-4 X -8}/_-4-8
Sin (2θ 30⁰) Cos 4θ⁰Sin (20 30⁰) Cos 4θ
Θ ¹²⁰⁰/₆=20⁰
Let 52x be U
5^2X(5³) 20(5^2X) =625
25U 20U = 625
125
^5U/₅ = ⁶²⁵/₅ U = 125
52x 53
2x = 3
X = ³/₂
The sum of n sides polygon in degrees (n -2) 180⁰Angles in quadrilateral add up to 3600
5(x+4)+4(x+5)+2(x+10)+(x+20)+360⁰
(x+20) = 360⁰12x = 360
X = 30⁰Interior angles
5(x+4)=170⁰
4(x+5)=140⁰
2(x+10)=40⁰
X+20=10⁰
Exterior angles
180⁰ 170⁰ 10⁰
180⁰ 140⁰ 40⁰
180⁰ 40⁰ 140⁰
180⁰ 10⁰ 170⁰No mark for 1 or less correct angles
¹⁴⁰/_¹⁰⁰ x 1240 =1736
Selling price
⁷⁵/₁₀₀x1736
Ksh 1302 B 1
Co-odinates A are (-1,7)
B are (3,-5)
C are (6,-4)
AB 3 - -1 4
5 7 -1
BC 0 - 3 -3
4 -5 9
4BC -3 -3 AB hence BC parallel to AB.
They share a common point B hence collinear.
(30cm3)
ASF ¹⁰⁸/₁₂LSF ASF 3
VSF (LSF3) 2
⁸¹⁰/_V1 27
V1 = ⁸¹⁰/₂₇= 30cm
1. Area of triangle ADB is ¹/₂ x 7 x 125 to 60°
  =7 x 6 sin 60⁰ = 36.37 cm2
2. Area of unshaded sector
  ⁶⁰/₃₆₀ x ²²/₇ x 7 x =25.6667
  Shaded area 36.37 25.67
  =10.7 cm2 B
-7 x X < 3x + 2 2x < 9,x7 4-5
3x+2<4(x 5), 3x + 2 < 4x 20
-x < -22, x > 22
If x > -5 and X>22
22
(3.5) (2p√x/_3X5)
(3x5)95² 4p²x x3x 5
27x 5² 455² 4p²x
27x5² - 4p²x 455²X(275² 4p²) 455²X 455²
2752 4p2
Max val of x 13.45 min 13.35
Max val of y 4.35 min 4.25
Max value of x 13.45 3.1647
Y 4.25
Max value of x 13.35 3.069
Y 4.35
Actual value of x 13.4 3.1163
Y 4.3
Absolute error 3.1642 3.069 = 0.04785
2
Pere em 0.04785 x100 0.015355x100
3.1163
1.5355%
Gradient of AB is M-1 M- 1
4 2 2
Gradient product is -1
Gradient of second line
Y 5 2x is 2
3 3
m-¹/₂ ³/₂2m -2 = 6
2m = 8
M = 4
Principal p amount 2p
2p p(I + 10)n 2p - p (1+0.1)n
100 p p
2 (1 1)n
Log 2 n log 1.1
N log 2 0.301
Log 1.1 0.0414
N = 7.27
Round upto 8
N = 8 yrs
P(black) and p(brown) or p(brown and p(black)
5 x 3 x 3 x 4
8 x 7 x 8 x 7
15 3
56 14
27
56
1. 400km
  Nairobi → busia
  Speed = 120 km/hr
  Distance = 400 km
  Time = ⁴⁰⁰/₁₂₀
  = 3hrs 20min
  8.30 + 3 hrs 20min
  11: 50 a.m
2. at 8.30 am distance covered by bus
  ½ x 80 = 40km
  Distance left = 360 km
  Speed = 2000km/hr
  Time = ³⁶⁰/₂₀₀ = 1 hr 48 min
  They met at 8.30 + 1 hr 48min
  10.18 am
3. 8 – 10.18 is 2 hrs 18min
  Distance = 2 x 80 + ¹⁸/₆₀ x 80
  160 +24
  184km from Nairobi.
4. Car arrived in Nairobi after 3 hrs 20 min bus travelled at a time of
  3hrs 20 min + 30 min
  = 3hrs 50 min
  Dist = 3 x 80 = ⁵⁰/₆₀ x 80
  = 240 + 66¹/₃
  = 931/3km
  Distance from Busia is 931/3 km
ABC
Y - = -x drawn
A¹B¹C¹ draw (rotated)
A¹¹B¹¹C¹¹ draw(translated)
A¹¹¹B¹¹¹C¹¹¹ Enlarged
A^1v(2,6) B^1v(0,0)C^1v(-6,2)
1. x²+x²=(56 -2x)²
  2x² = 4x²– 224x + 3136
  2x²- 224 x + 3136 = 0
  X² – 112x + 1568 = 0
  X ( x –16) – 98 (x – 16) = 0
  (x-16) ( x – 98) =0
  X = 16 or 98
  Height = 16 cm
  Tan θ = ¹⁶/₃₅=0.4575
  = 24.57^o
2. ST = √162 + 352
  = √1481
  = 38.48
3. Muximum distance
  = 35 ± 16
  = 51
1. 50,00+⁶/₁₀₀x62 5000 + 10000 x 250
  50,000 + 37500 + 25,000
  = 112,5000
2. 1. 12000 x 2.5+0.06x+50,000 =134 000
    30,00 + 50,000 + 0.06x = 134 000
    0.06x = 134 000 – 80 000
    ^0.06/_0.06x = ⁵⁴⁰⁰⁰/_0.06x = 900,000
  2. increase = 900 000 – 625 000
    = 275,000
    % increase = ^{275 000}/_{625 000} x 100
    = 44 %
Distance covered in 90 min
Bl P = 540km
Q = 360 km
Scale 1 cm = 10 000 000 cm
1 cm rep 100 km

Distance btwn plane 2,1 cm ± 0.1
2 10 ± 10
Bearing of plane Q from plane P
185 ± 1°
1. ⁴⁰/₂₄ =x+56
  40 =24x+1344
  x = 84
  vol = ²⁷/₃x¹/₃X40₂X140–²²/₇ x¹/₃ x242x84
  = ^183978.67/₁₀₀₀= 183.978 litres
2. ⁴⁰/₁₄₀ = ^r/_h²/₇=^r/_hh =⁷r/₂³/₄ x²²/₇x¹/₃(402x140–24²x 84) =²²/₇ x1(7r³– 24² x84)
  ³/₄ (40²x140–24₂ x84)=^7r3/₂– 24² x84)
  ³/₄ x 175516 =^7r3/₂– 48384
  180096 x ²/₇ =r³³√r³ = ³√51456
  r = 37,19 M1
1. ACC = ^15–0/₂₀= 0.75m/s²
2. Dece = ^{0 – 15}/₂₀= - 0.75
3. Area = ¹/₂x 20 x 15
  = 150ml
4. Area=20x15
  = 300m
5. Area = ¹/₂(30+60)X15
  = 675m