Mathematics Paper 1 Questions and Answers - Form 4 Term 1 Opener Exams 2021

FORM 4 TERM 1
OPENER EXAMS
MATHEMATICS PAPER 1
TIME: 2½ HRS.

INSTRUCTION TO STUDENTS:

• This paper consists of two Sections; Section I and Section II.
• Answer ALL the questions in Section I and only five questions from Section II.
• Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
• Marks may be given for correct working even if the answer is wrong.
• KNEC Mathematical tables may be used, except where stated otherwise.
• Candidates should answer the questions in English.

SECTION I (50 marks)

1. Without using a calculator, evaluate. (3 marks)
   -8+(-5) x(-8)-(-6)
   -3+(-8) ÷ 2 x 4
2. Evaluate without using a calculator (2 marks)
   
3. In fourteen years time, a mother will be twice as old as her son. Four years ago, the sum of their ages was 30 years. Find how old the mother was, when the son was born.( 4 marks)
4. A Kenya bank buys and sells foreign currencies as shown below
   

   	Buying (In KShs)	Selling (In Kshs)
   1 Hong Kong dollar	9.74	9.77
   1 South African rand	12.03	12.11

   A tourist arrived in Kenya with 105000 Hong Kong dollars and changed the whole amountto Kenyan shillings. While in Kenya, she spent Kshs. 403,897 and changed the balance to South Africa rand before leaving for South Africa. Calculate the amount, in South African rand that she received. (3 marks)
5.    
   1. Using a ruler and a pair of compasses only, construct a quadrilateral PQRS in which PQ= 5cm, PS = 3cm, QR = 4cm,<PQR = 135°and <SPQ is a right angle. (2 marks)
   2. The quadrilateral PQRS represents a plot of land drawn to a scale of 1:4000. Determine the actual length of RS in meters. (2 marks)
6. The ratio of goats to cows in a farm is 2:5 while the ratio of sheeps to cows is 3:4. If there are 15 sheep, how many animals are there in farm?(2 marks)
7. Mr.Maina who deals in electronics sells a radio to a customer at Ksh. 1440 after giving a discount of 10% but find that he makes a 20% profit. Find the profit Mr. Maina would make if he does not give a discount. (3 marks)
8. Use the reciprocal and square table to evaluate to four significant figure, the expression.(3 marks)
   
9. Simplify the following expression completely. (3 marks)
   
10. Given that sin (x + 60)° = Cos (2x)°, find tan (x + 60)°. (3 marks)
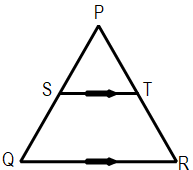
11. The figure below shows triangle PQR in which PR = 12 cm, T is a point on PR such that TR = 4cm. line ST is Parallel to QR
    
    If the area of triangle PQR is 336 cm², find the area of the quadrilateral QRTS. (3 marks)
12. A square brass plate is 2 mm thick and has a mass of 1.05 kg. The density of the brass is 8.4 g/cm³. Calculate the length of the plate in centimeters (3 marks)
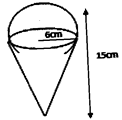
13. The diagram below represent a solid made up of a hemisphere mounted on a cone. The common radius is 6 cm and the height of the solid is 15cm.
    
    Calculate the external surface of the solid (4 marks)
14. Solve the simultaneous inequalities given below and list all the integral values of x (3 marks)
    ^3-x/₂≥^x+1/₃≥^2x+1/_-3
15. A construction company employs technicians and artisans. On a certain 3 technicians and 2 artisans were hired and paid a total of Ksh 9,000.
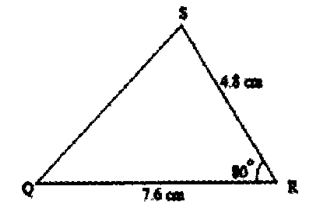
    On another day the firm hired 4 technicians and one artisan and paid a total of Ksh 9500. Calculate the cost of hiring two technicians and 5 artisans in a day
16. The figure below is not drawn to scale.
    
    Find correct to 1 decimal place;
    1. Length PQ. (2 marks).
    2. Angle ABC (2 marks)

SECTION II(50 marks)
CHOOSE ANY FIVE QUESTIONS IN THIS SECTION

17. Two lines L1: 2y - 3x - 6 = 0 and L2: 3y+x-20 = 0 intersect at point A.
    1. Find the coordinates of A. (3 marks)
    2. A third line L₃ is perpendicular to L₂ at point A. Find the equation of L₃ in the form y = mx +c, where m and c are constants. (3 marks)
    3. Another L₄ is parallel to L₁ and passes through (-1, 3). Find the x and y intercepts of L₄ (4 marks)
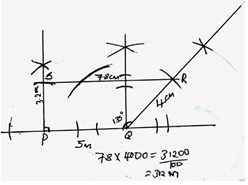
18. Town B is 180km on a bearing 050⁰ from town A. Another town C is on a bearing of 110° from town A and on a bearing of 150° from town B. A fourth town D is 240 km on a bearing of 320° from A. Using scale drawing, such that 1cm rep 30km,
    1. Show the relative position of the towns (4 marks)
    2. Using the diagram, find
       1. Distance AC (2 marks)
       2. Distance CD (2 marks)
       3. Compass bearing of C from D (2 marks)
19. The table shows the marks obtained by 40 candidates in an examination
    

    Marks	5-14	15-29	30-34	35-44	45-49
    Frequency	2	12	7	15	x

    
    
    1. Find the value of X (1 mark)
    2. Calculate the mean mark (2 marks)
    3. On the grid provided below draw a histogram to represent the data (4 marks)
    4. drawing a straight line on the graph above determine the median mark (3 marks)
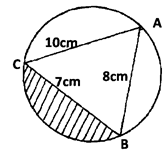
20. The figure below shows a triangle ABC inscribed in a circle. AC = 10cm, BC = 7cm and AB = 10cm.
    
    
    1. Find the size of angle BAC. (3 marks)
    2. Find the radius of the circle. (2 marks)
    3. Hence calculate the area of the shaded region. (5 marks)
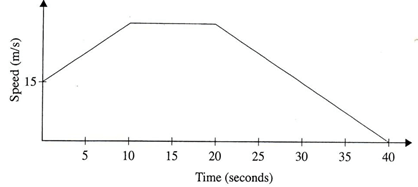
21. The figure below represents a speed time graph for a cheetah which covered 825m in 40 seconds.
    
    
    1. State the speed of the cheetah when recording of its motion started (1 mark)
    2. Calculate the maximum speed attained by the cheetah (3 marks)
    3. Calculate the acceleration of the cheetah in:
       1. The first 10 seconds (2 marks)
       2. The last 20 seconds (1 mark)
    4. Calculate the average speed of the cheetah in first 20 seconds (3 marks)
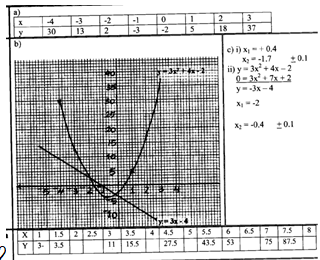
22. Given the quadratic function y=3x² + 4x - 1
    1. Complete the table below for values of x ranging - 4≤ x ≤3. (2 marks)
       

       X	-4	-3	-2	-1	0	1	2	3
       Y

    2. Using the grid provided draw the graph of y = 3x² + 4x —2 for -4≤ x ≤ 3 (3 marks)
    3. Using the graph, find the solution to the equations.
       1. 3x²+4x-2=0 (2 marks)
       2. 3x²+7x+2=0 (3 marks)
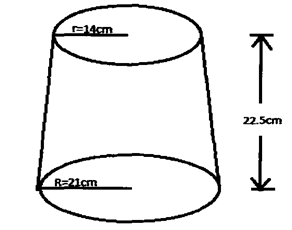
23. The diagram represents a solid frustum with base radius 21cm and top radius 14cm. The frustum is 22.5cm high and is made of a metal whose density is 3 g/cm³.
    (Take π=²²/₇)
    
    
    1. Calculate
       
       1. The volume of the metal in the frustum. (5 marks)
       2. The mass of the frustum in kg. (2 marks)
    2. The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost. Calculate to 2 decimal places the length of each side of the cube.(3 marks)
24. A saleswoman is paid a commission of 2% on goods sold worth over Ksh 100,000. She is also paid a monthly salary of Ksh 12,000.In a certain month, she sold 360 handbags at Ksh 500 each.
    1. Calculate the saleswoman’s earnings that month. (3 marks)
    2. The following month, the saleswoman’s monthly salary was increased by 10%. Her total earnings that month were Ksh 17,600.
       Calculate:
       1. The total amount of money received from the sales of handbags that month.(5 marks)
       2. The number of handbags sold that month. (2 marks)
          
          
          

MARKING SCHEME

SECTION I (50 marks)

1. Without using a calculator, evaluate. (3 marks)
   -8+(-5) x(-8)-(-6)
   -3+(-8) ÷ 2 x 4
   
   -8 -5 x -8 +6
   -8 + 40 +6
   =38   
   
   -3 – 8 ÷ 2 x 4
   -3 – 4 x 4 = -19
   ^{= 38}/_-19
   = -2
   
   
2. Evaluate without using a calculator (2 marks)
   
   ¹⁷/₇ - ¹¹/₆ = ²⁵/₄₂ X ⁶/₅ = ⁵/₇
   ²/₃ X ⁹/₄ = ³/₂ - ⁸/₇ = ¹⁵/₁₄
   ⁵/₇ X ¹⁴/₅ = 2
   
   
3. In fourteen years time, a mother will be twice as old as her son. Four years ago, the sum of their ages was 30 years. Find how old the mother was, when the son was born.( 4 marks)
   Let mother's years be x and son's be y
   x+14= 2(y +14)
   x+14= 2y + 28
   x-2y = 14
   
   (x-4)+(y-4) = 30
   x +y = 38
   
      (x- 2y= 14)
     -(x+ y= 38)
   = -3y=-24
   =3y=24
   y=8( son's age currently)
   x+y=38
   x=30( mother's age currently)
   At son's birth, mother's age = 30-8=22 years
   
   
4. A Kenya bank buys and sells foreign currencies as shown below
   

   	Buying (In KShs)	Selling (In Kshs)
   1 Hong Kong dollar	9.74	9.77
   1 South African rand	12.03	12.11

   A tourist arrived in Kenya with 105000 Hong Kong dollars and changed the whole amount to Kenyan shillings. While in Kenya, she spent Kshs. 403,897 and changed the balance to South Africa rand before leaving for South Africa. Calculate the amount, in South African rand that she received. (3 marks)
   105000 x 9.74 = 1,022,700
   ^{(1022700 - 403879)}/₅₁₁₀₀
   
   
5.    
   1. Using a ruler and a pair of compasses only, construct a quadrilateral PQRS in which PQ= 5cm, PS = 3cm, QR = 4cm,<PQR = 135°and <SPQ is a right angle. (2 marks)
   2. The quadrilateral PQRS represents a plot of land drawn to a scale of 1:4000. Determine the actual length of RS in meters. (2 marks)
      
      
      
6. The ratio of goats to cows in a farm is 2:5 while the ratio of sheeps to cows is 3:4. If there are 15 sheep, how many animals are there in farm?(2 marks)
   Goats(G), Cows(C), Sheep(S)
   G:C:S
   2:5
       4 :3
   G :C  : S
   8 :20:15
   sheep = 15
   15+20+8= 43 Animals
   
   
7. Mr.Maina who deals in electronics sells a radio to a customer at Ksh. 1440 after giving a discount of 10% but find that he makes a 20% profit. Find the profit Mr. Maina would make if he does not give a discount. (3 marks)
   
   100% = x
   90% = 1440
   

   1440 x 100
         90
   =1600

   120% =1600

   100% =x
   
   1600 x 100
         120
   =1333.3
   1600 – 1333.3 = 266.70

8. Use the reciprocal and square table to evaluate to four significant figure, the expression.(3 marks)
   
   ¹/_0.03654 - 4.151²
   4.151² = 17.231
   ¹/_0.03654 = ¹/_{3.654 x 10^-2}= ¹/_3.654 x ¹/_10^-2
   0.237 x 10² = 27.37
   27.37 - 17.231=10.139
   
   
9. Simplify the following expression completely. (3 marks)
   
   12a² - 3b² = 3(2a +b)(2a-b)
   2a²-ab-b² = 2a(a-b)+b(a-b)
   3(2a +b)(2a-b)
   2a(a-b)+b(a-b)
    =3(2a-b)
        a-b
   = ^3(2a-b)/_a-b
   
   
10. Given that sin (x + 60)° = Cos (2x)°, find tan (x + 60)°. (3 marks)
    Sin x+ 60º = Cos 2x
    x+ 60 + 2x =90
    3x = 30
    x=10
    Tan (x+60)= Tan 70
    Tan 70 = 2.748, 2.7475
    
    
11. The figure below shows triangle PQR in which PR = 12 cm, T is a point on PR such that TR = 4cm. line ST is Parallel to QR
    
    If the area of triangle PQR is 336 cm², find the area of the quadrilateral QRTS. (3 marks)
    12-4 = 8
    ¹²/₈= ³/₂
    a.s.f = ⁹/₁₂
    ⁴/₉ x 336 = 149¹/₃
    Area QRST = 336- 149 ¹/₃ = 186 ²/₃
12. A square brass plate is 2 mm thick and has a mass of 1.05 kg. The density of the brass is 8.4 g/cm3. Calculate the length of the plate in centimeters (3 marks)
    Volume = mass/density 
    1050cm3/8.4 = 125 cm3
    ∴ L x L x 0.2 cm = 125 cm3

    L² = ^{(125 cm)}/_0.2 = 625
    L = √(625 ) = 25 cm

13. The diagram below represent a solid made up of a hemisphere mounted on a cone. The common radius is 6 cm and the height of the solid is 15cm.
    
    Calculate the external surface of the solid (4 marks)
    2 x 3.142 x 36 = 226.224
    3.142 x 610.82 = 204.0
    Total = 430.224cm
    
    
14. Solve the simultaneous inequalities given below and list all the integral values of x (3 marks)
    ^3-x/₂≥^x+1/₃≥^2x+1/_-3
    9-3x>2x +2
    7/5 >x
    x+1>-2x -1
    x > ^-2/₃
    ^-2/₃ < x < 1²/₅
    3x > -2
    
    
15. A construction company employs technicians and artisans. On a certain 3 technicians and 2 artisans were hired and paid a total of Ksh 9,000.
    On another day the firm hired 4 technicians and one artisan and paid a total of Ksh 9500. Calculate the cost of hiring two technicians and 5 artisans in a day
    

    3t+2a=9000..... (i)
    4t+a =9500...... (ii)
    Multiply (ii)x2
    8t+2a =19000-
    3t+2a =9000
    5t = 10000
    t = 2000√
    substituting in (i) above
    3 x 2000 + 2a = 9000
    a = ³⁰⁰⁰/₂
    a = 1500√
    t = 2000
    2 x 2000 + 5 x 1500=11500

16. The figure below is not drawn to scale.
    
    Find correct to 1 decimal place;
    1. Length PQ. (2 marks).
        7.6² + 4.8² – 2 x 7.6 x 4.8 cos 80
       = 57.76 + 23.04 – 12.67
       = 68.13 
       R = 68.13
       = 8.3
       
       
    2. Angle ABC (2 marks)
       ^{Sin B}/ _4.8 = ^Sin 80/_8.254
       SinB = 0.5727
       B = sin -10.5727
       = 34.9^{0
       .}

SECTION II(50 marks)
CHOOSE ANY FIVE QUESTIONS IN THIS SECTION

17. Two lines L1: 2y - 3x - 6 = 0 and L2: 3y+x-20 = 0 intersect at point A.
    1. Find the coordinates of A. (3 marks)
       2y – 3x = 6
       3y + x = 20
       2y - 3x = 6
       9y + 3x = 60
       11y = 60
       Y= 6
       X = 20 -18
       = 2
       Co-ordinates of A are (2,6)
       
       
    2. A third line L₃ is perpendicular to L₂ at point A. Find the equation of L₃ in the form y = mx +c, where m and c are constants. (3 marks)
        L2: 3y = -x + 20
       y = - 1/3 x + 20 
       Gradient of perpendicular = 3
       ^(y-6)/_(x-2) =3
       Y= 3X- 6 + 6
       Y = 3X
       
       
    3. Another L₄ is parallel to L₁ and passes through (-1, 3). Find the x and y intercepts of L₄ (4 marks)
       Gradient of L₄= gradient of L₁
       =³/₂
       ^(y-3)/_(x-1) = ³/₄
       2y -6 = 3X + 3
       2y - 3X = 9
       When X = 0 y = 4.5
       When y = 0 x = -3
       
       
18. Town B is 180km on a bearing 050⁰ from town A. Another town C is on a bearing of 110° from town A and on a bearing of 150° from town B. A fourth town D is 240 km on a bearing of 320° from A. Using scale drawing, such that 1cm rep 30km,
    1. Show the relative position of the towns (4 marks)
    2. Using the diagram, find
       1. Distance AC (2 marks)
       2. Distance CD (2 marks)
       3. Compass bearing of C from D (2 marks)
          (representation, not to scale)
          
19. The table shows the marks obtained by 40 candidates in an examination
    

    Marks	5-14	15-29	30-34	35-44	45-49
    Frequency	2	12	7	15	x

    
    
    1. Find the value of X (1 mark)
       4
       
    2. Calculate the mean mark (2 marks)
       ^Σfx/_Σf = ^1287.5/₄₀ = 32.1875
       
    3. On the grid provided below draw a histogram to represent the data (4 marks)
       

       CB	4.5 - 14.5	14.5 -29.5	29.5 - 34.5	34.5 - 44.5	44.5 - 49.5
       Fd	0.2	0.8	1.4	1.5	0.8
       Fx	19	264	224	595.5	188

       
       
    4. drawing a straight line on the graph above determine the median mark (3 marks)
       total area A = 10 x 0.2 = 2 
       B= 15 x 0.8 = 12
       C = 1.4 x y = 6 
       D = 1.5 x 10 = 15
       E = 0.8 x 5 = 4
       2 + 12 + 7 + 15 + 4 = ⁴⁰/₂= 20
       Point to draw the lie is 29.5 + ⁶/₇ =30.36
       
       
20. The figure below shows a triangle ABC inscribed in a circle. AC = 10cm, BC = 7cm and AB = 10cm.
    
    
    1. Find the size of angle BAC. (3 marks)
       a² =b²+ c² – 2bc cos A
       7² = 10² + 8² - (2 x 10 x 8) cos A
       49=164- 60 cos A
       -116 =160 cos A
       Cos A =¹¹⁶/₁₆₀
       Cos A = 0.725
       Cos¹ 0.725 = 43.53115
       <BAC = 43.53
       
       
    2. Find the radius of the circle. (2 marks)
       ^a/_{(sin sin A )} = 2R
       ⁷/_{(sin 43.53)} = 2R
       R =5.082cm
       
       
    3. Hence calculate the area of the shaded region. (5 marks)
       Sin 43.53 = ^3.5/_r
       r = ^3.5/_{(sin sin 43.53 )}= 5.082 cm
       Area of △OCB =¹/₂ ab sin θ
       = 1/2 x 5.082 sin 87.06
       = 12.896cm²
       Area of sector ACB
       =θ/360 πr²
       =^87.06/₃₆₀ x ²²/₇ x 5.082 = 19.630
       Shaded region
       (19.630 — 12.896) = 6.734 cm²
       
       
       
21. The figure below represents a speed time graph for a cheetah which covered 825m in 40 seconds.
    
    
    1. State the speed of the cheetah when recording of its motion started (1 mark)
       15m/s
       
    2. Calculate the maximum speed attained by the cheetah (3 marks)
       ¹/₂ (15+h)×10+¹/₂ (10+30)h=825
       75+5h+20h=825
       25h=750
       
       
    3. Calculate the acceleration of the cheetah in:
       1. The first 10 seconds (2 marks)
          h=30m/s(i) = ^(30-15)/₁₀
          = 1.5m/s²
       2. The last 20 seconds (1 mark)
          ^0-30/₂₀ = -1.5m/s²
          
    4. Calculate the average speed of the cheetah in first 20 seconds (3 marks)
       [¹/₅ (15+30)×10+10×30]÷20
       = (225+300)÷20
       =26.25 m/s
       
       
22. Given the quadratic function y=3x² + 4x - 1
    1. Complete the table below for values of x ranging - 4≤ x ≤3. (2 marks)
       

       X	-4	-3	-2	-1	0	1	2	3
       Y	30	13	2	-3	-2	5	18	37

    2. Using the grid provided draw the graph of y = 3x² + 4x —2 for -4≤ x ≤ 3 (3 marks)
    3. Using the graph, find the solution to the equations.
       1. 3x²+4x-2=0 (2 marks)
       2. 3x²+7x+2=0 (3 marks)
          
23. The diagram represents a solid frustum with base radius 21cm and top radius 14cm. The frustum is 22.5cm high and is made of a metal whose density is 3 g/cm³.
    (Take π=²²/₇)
    
    
    1. Calculate
       
       1. The volume of the metal in the frustum. (5 marks)
          Volume
          Ratio ^x/₁₄ =^(22.5+x)/₂₁
          21X=14(22.5 +X)
          21= 14(22.5 + x)
          21x - 14x = 315
          x = 45cm
          Volume of whole cone
          =1/3 x 22/7 x 21 x 21 x 67.5 =31185 cm³
          Volume of small cone
          =1/3 x 22/7 x14 x 14 x 45 = 9240 cm³ 
          Volume of frustum
          31185- 9240 = 21 945 cm³
          
          
       2. The mass of the frustum in kg. (2 marks)
          Mass of frustum
          Mass=21945x3g/cm³ =65835g 
          Mass in kg= ^{(65.835 g)}/_1000g = 65835kg
          
          
    2. The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost. Calculate to 2 decimal places the length of each side of the cube.(3 marks)
       20% of 65.835kg = 13.167 kg
       65.835 - 13.167 = 52.668 kg
       Volume of material remaining =
       ⁵⁶⁶⁸²/₃= 17556cm³
       Length of cube = ∛(17 556 )= 25.99 cm
       
       
24. A saleswoman is paid a commission of 2% on goods sold worth over Ksh 100,000. She is also paid a monthly salary of Ksh 12,000.In a certain month, she sold 360 handbags at Ksh 500 each.
    1. Calculate the saleswoman’s earnings that month. (3 marks)
       360x500=180,000
       180,000-100,000= 80,000
       80,000x²/₁₀₀ = 1600
       12000+1600=13600
       
       
    2. The following month, the saleswoman’s monthly salary was increased by 10%. Her total earnings that month were Ksh 17,600.
       Calculate:
       1. The total amount of money received from the sales of handbags that month.(5 marks)
          12000x¹¹⁰/₁₀₀=13200 - basic salary
          17600-13200 =4400
          4400x100/2 = 220,000
          220,000+100,000= 320,000
          
          
       2. The number of handbags sold that month. (2 marks)
          320,000/500 = 640