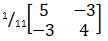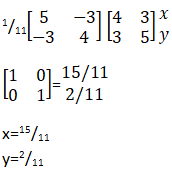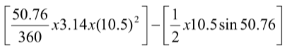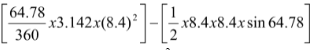MATHEMATICS
FORM 4
END TERM EXAMS
TERM 1 2021
PAPER 1
TIME 2½ hrs
INSTRUCTIONS
- This paper has two sections: Section I and II
- Answer all questions in Section I and and FIVE in Section II
SECTION I (50 MARKS)
Answer all the questions in this section
- A boy cycles a certain distance from X to Y at 10km/hr, he returns at 12km/hr. The total time taken is 1hr 50min. find the distance XY. (3marks)
- Simplify p2 – 2pq + q2 (3marks)
____________
2p2 -3pq + q2 - Solve for X in the equation. (3marks)
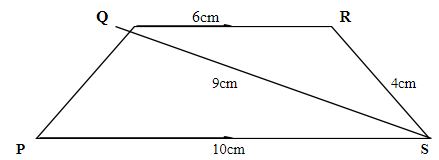
½ log2 81 + log2 (x2 – x/3) = 1 - In the figure below PQRS is a trapezium with QR parallel to PS.QR=6cm, RS=4cm, QS=9cm and PS=10cm
Calculate- The size of angle SQR (2marks)
- The area of triangle PQS (2marks)
- Find the value of x in the equation. (3marks)
COS (3x – 180º) = √3/2 in the range 0º≤ x ≤ 180º - A famer has a piece of land measuring 840m by 396m. He divides it into square plots of equal sizes. Find the maximum area of one plot. (3marks)
- A liquid spray of 384g is packed in a cylindrical container of internal radius 3.2cm. Given that the density of the liquid is 0.6g/cm3, calculate to 2 decimal places the height of the liquid in the container. (3marks)
-
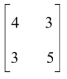
- Find the inverse of the matrix. (1mark)
- Hence solve the simultaneous equation using the matrix method. (2marks)
4x+3y=6
3x+5y=5
- Find the inverse of the matrix. (1mark)
- Two pipes A and B can fill an empty tank in 3hrs and 5hrs respectively. Pipe C can empty the tank in 4hrs. If the three pipes A, B and C are opened at the same time find how long it will take for the tank to be full. (3marks)
- A tourist arrived in Kenya with sterling pound (£) 4680 all of which he exchanged into Kenyan money. He spent Ksh.51790 while in Kenya and converted the rest of the money into US dollars. Calculate the amount he received in US dollars. The. Exchange rates were as follows. (4marks)
Buying Selling US dollars $ 65.20 69.10 Sterling pounds £ 123.40 131.80 - The gradient of a straight line L1, passing through the point P (3, 4) and Q (a, b) is -3/2. A line L2 is perpendicular to L1 through Q and R (2, -1). Determine the values of a and b. (3marks)
- Find the number of sides of a regular polygon whose interior angel is 5 times the exterior angle.(3marks)
- The points A, B and C lie on a straight line. The position vectors of A and C are 2i + 3j + 9k and 5i - 3j + 4k respectively; B divides AC internally in the ratio 2:1 Find the:
- Position vector of B (2marks)
- Distance of B from the Origin (1mark)
- The sum of digits in a two digit number is 16. When the number is subtracted from the number formed by reversing the digits the difference is 18. Find the number. (3marks)
- In Blessed Church Choir the ratio of males to females is 2:3. On one Sunday service ten male members were absent and six new female members joined the choir as guests for the day. If on this day the ratio of males to females was 1:3, how many regular members does the choir have? (3marks)
- A businessman makes a profit of 20% when he sells a carpet for Ksh. 36000. In a trade fair he sold one such carpet for Ksh. 33600. Calculate the percentage profit made on the sale of the carpet during the trade fair. (3marks)
SECTION II:(50 MARKS)
Answer any FIVE questions in this section
- A Matatu and a Nissan left town A for town B 240km away at 8.00am travelling at a speed of 90km/hr and 120 km/h respectively. After 20minutes the Nissan had a puncture which took 30minutes to mend.
- How far from town A did the Nissan catch up with the Matatu? (6marks)
- At what time did the Nissan catch up with the Matatu? (1mark)
- At what time did the Matatu reach town B (3marks)
- The displacement, S metres of a moving particle from point O, after t seconds is given by:
S = t3 – 5t2 + 3t + 10- Find S when t = 2 (2marks)
- Determine:
- The velocity of the particle when t = 5sec (3marks)
- The value of t when the particles is momentarily at rest . (3 marks)
- Find the time, when the velocity of the particle is maximum. (2 marks)
- Four towns P, R, T and S are such that R is 80km directly to the north of P and T is on a bearing of 290° from P at a distance of 65km. S is on a bearing of 330° from T and a distance of 30 km. Using a scale of 1cm to represent 10km, make an accurate scale drawing to show the relative position of the towns. (4mks)
Find:- The distance and the bearing of R from T (3mks)
- The distance and the bearing of S from R (2mks)
- The bearing of P from S (lmk
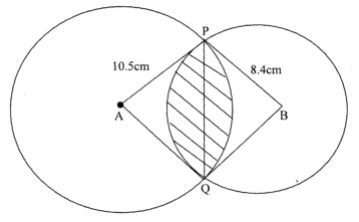
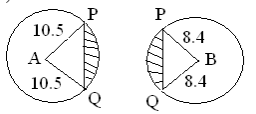
- The figure below shows two circles of radii 10.5 and 8.4cm and with centres A and B respectively. The common chord PQ 9cm.
- Calculate angle PAQ. (2 mks)
- Calculate angle PBQ. (2 mks)
- Calculate the area of the shaded part. (6 mks)
- The following measurement were recorded in a field book using XY as the baseline. XY = 400m.
Y C60 340 300 1200 240 160E 220 160F B100 140 A120 80 X - Using a scale of 1:4000 draw an accurate map of the farm. (4 marks)
- Determine the actual area of the farm in hectares. (4 marks)
- If the farm is on sale at sh.80,000 per hectare find how much the farm costs.(2marks)
- The length and breadth of a rectangle are given as (6x - 1) and (x -2) metres respectively. If the length and breadth are each increased by 4 metres, the new area is three times that of original rectangle.
- Form an equation in x and solve it. (4 marks)
- Find the dimensions of the original triangle (2 marks)
- Express the increase in area as a percentage of the original area. (4 marks)
- X, Y and Z are three quantities such that X varies directly as the square of Y and inversely as the square root of Z.
- Given that X = 18 when Y = 3 and Z = 4, find X when Y = 6 and Z = 16. (5 marks)
- If Y increases by 10% and Z decreases by 19%, find the percentage increase in X. (5 marks)
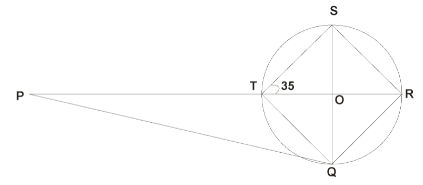
- The diagram below a circle, centre O. PQ is a tangent to the circle at Q and PTOR is a straight line. QRST is a cyclic quadrilateral in which angle RTS = 350 and RT and QS are diameters. Giving reasons for your answer, find the size of:
- Acute angle ROS. (2marks)
- Angle RQS. (2 marks)
- Angle PQR. (2 marks)
- Angle QPT. (2 marks)
- Angle PQT. (2 marks)

MARKING SCHEME
SECTION I (50 MARKS)
Answer all the questions in this section
- A boy cycles a certain distance from X to Y at 10km/hr, he returns at 12km/hr. The total time taken is 1hr 50min. find the distance XY. (3marks)
- Let distance be x
Time= distance/speed
Time to = x/10 hrs
Time from = x/12 hrs
Total time
x/10+x/12= 110/60
x/10+x/12=11/6
12x+10x=11x20
22x=220
x=10km
- Let distance be x
- Simplify p2 – 2pq + q2 (3marks)
____________
2p2 -3pq + q2
- P2-pq-pq+q2
p (p-q)-q(p-q)
(P-q)2 - 2p2-3pq+q2=
2p2-2pq-pq-q2=
2p(p-q)-q(p-q)=
(2p-q) (p-q)
(p-q) (p-q) = p-q
(2p-q)(P-q) 2p-q
p-q/2p-q
- P2-pq-pq+q2
- Solve for X in the equation. (3marks)
½ log2 81 + log2 (x2 – x/3) = 1- Log29 +log2(x2-x/3)=log22
9x2-3x-2=0
9x2-6x+3x-2=0
3x(3x-2) +1(3x-2)=0
X=2/3 or -1/3
- Log29 +log2(x2-x/3)=log22
- In the figure below PQRS is a trapezium with QR parallel to PS.QR=6cm, RS=4cm, QS=9cm and PS=10cm
Calculate- The size of angle SQR (2marks)
- 42=92+62-2 x 6 x 9 cosQ
108cosQ=101
Q = cos 10.9352
Q =20.74º
- 42=92+62-2 x 6 x 9 cosQ
- The area of triangle PQS (2marks)
- area of PQS
= ½ x 9 x 10 sin 20.740
= 15.94cm2
- area of PQS
- The size of angle SQR (2marks)
- Find the value of x in the equation. (3marks)
COS (3x – 180º) = √3/2 in the range 0º≤ x ≤ 180º- Cos (3x-180º)= √3/2
3x -180 = 30
3x = 210
X= 70º
- Cos (3x-180º)= √3/2
- A famer has a piece of land measuring 840m by 396m. He divides it into square plots of equal sizes. Find the maximum area of one plot. (3marks)
- 840=23x 3 x 5 x 7
396=22 x 32 x 11
GCD=22 x 3=12
Area =12 x 12
= 144cm2
- 840=23x 3 x 5 x 7
- A liquid spray of 384g is packed in a cylindrical container of internal radius 3.2cm. Given that the density of the liquid is 0.6g/cm3, calculate to 2 decimal places the height of the liquid in the container. (3marks)
- Mass of spray = 384
Intense radius =3.2
Density of = 0.6g/lcm2
V= M/D= 384g/0.6glc= 640cm3
Volume of the cylinder= π2h
π2h= 640
3.142x 3.22 h= 640
h2= 640 = 640
3.142x 3.22 3.142 x 10.24
= 640/32.17408
=19.891789
= 19.89cm
- Mass of spray = 384
-
- Find the inverse of the matrix. (1mark)
Det= 20-9=11
inverse = - Hence solve the simultaneous equation using the matrix method. (2marks)
4x+3y=6
3x+5y=5
- Find the inverse of the matrix. (1mark)
- Two pipes A and B can fill an empty tank in 3hrs and 5hrs respectively. Pipe C can empty the tank in 4hrs. If the three pipes A, B and C are opened at the same time find how long it will take for the tank to be full. (3marks)
- 1/9 +1/5 -1/4 = 20+12-18/60
= 17/60
17/60=1hr
1= 1 x 60/17
60/17 = 3.5294118
= 3.529 hrs
- 1/9 +1/5 -1/4 = 20+12-18/60
- A tourist arrived in Kenya with sterling pound (£) 4680 all of which he exchanged into Kenyan money. He spent Ksh.51790 while in Kenya and converted the rest of the money into US dollars. Calculate the amount he received in US dollars. The. Exchange rates were as follows. (4marks)
Buying Selling US dollars $ 65.20 69.10 Sterling pounds £ 123.40 131.80 - 4680 x 123140
= Ksh 577512
Remaining
557512-51790
Kshs 525,722
= 525,722
69.10
= US£ 608.13
- 4680 x 123140
- The gradient of a straight line L1, passing through the point P (3, 4) and Q (a, b) is -3/2. A line L2 is perpendicular to L1 through Q and R (2, -1). Determine the values of a and b. (3marks)
- 4-6/3-9= -3/2 and b+1/a-2 = 2/3
3a +2b=17
-2a+3b=-7
6a+4b=34
-6a+9b=-21
13b=13
b=1
a=5
- 4-6/3-9= -3/2 and b+1/a-2 = 2/3
- Find the number of sides of a regular polygon whose interior angel is 5 times the exterior angle.(3marks)
- x/5x
bx=180º
x=30º
no of sides =180/30
= 12sides
- x/5x
- The points A, B and C lie on a straight line. The position vectors of A and C are 2i + 3j + 9k and 5i - 3j + 4k respectively; B divides AC internally in the ratio 2:1 Find the:
- Position vector of B (2marks)
- OB= 1/3 2 + 5
3 -3
9 + 2/3 4
2/3 + 10/3
1 -2
3 -8/3
= 4
-1
17/3
- OB= 1/3 2 + 5
- Distance of B from the Origin (1mark)
- 0B = √42+ (-1)2+ (17/3)2
_________________
√ 1b +1+32.11
= √49.11
=7.007 square units
- 0B = √42+ (-1)2+ (17/3)2
- Position vector of B (2marks)
- The sum of digits in a two digit number is 16. When the number is subtracted from the number formed by reversing the digits the difference is 18. Find the number. (3marks)
- Let 10th digit be x
0 x =y
X+y=1b(i)
10y +a –(10x +y) =18
10y+x-10x-y=18
9y-9x=18
y-x=2(ii)
y+x=18
y+x=16
2y 0=18
Y=9
X=7
Number
79
- Let 10th digit be x
- In Blessed Church Choir the ratio of males to females is 2:3. On one Sunday service ten male members were absent and six new female members joined the choir as guests for the day. If on this day the ratio of males to females was 1:3, how many regular members does the choir have? (3marks)
- m/F= 2/3
m=2/3p
M-10 = 1/3
f+6
3m-30=F+6
M=f/3+12
= f/3+12= 2/3 f
F+36=2f
F=36
M=2/3 x36
= 24
Total 36+24=60
- m/F= 2/3
- A businessman makes a profit of 20% when he sells a carpet for Ksh. 36000. In a trade fair he sold one such carpet for Ksh. 33600. Calculate the percentage profit made on the sale of the carpet during the trade fair. (3marks)
- 120% =Ksh 36,000
100% = 100 x 3600
120
Kshs 36,000
Profit = 76,000
% profit = 36000 x 100 - 30,000
= 12%
- 120% =Ksh 36,000
SECTION II:(50 MARKS)
Answer any FIVE questions in this section
- A Matatu and a Nissan left town A for town B 240km away at 8.00am travelling at a speed of 90km/hr and 120 km/h respectively. After 20minutes the Nissan had a puncture which took 30minutes to mend.
- How far from town A did the Nissan catch up with the Matatu? (6marks)
- M2 90 kms/hr
A 40km b
8.00am 8.20 240km
D n=20/60 x 120 = 40km
Dm = 50/60 x 90 = 75km
Difference = 75-40
35km
Time to
35/120ups = 35/30
= 1 /6
= 1 hir 10mins
D = 35/30 x 120 = 140km
140+40=180km
From A
- M2 90 kms/hr
- At what time did the Nissan catch up with the Matatu? (1mark)
Time .8.50
1.10
10.00a.m - At what time did the Matatu reach town B (3marks)
- T-240/90 = 2hrs 40mins
Time = 8.00am
2.40
10.40 am
- T-240/90 = 2hrs 40mins
- How far from town A did the Nissan catch up with the Matatu? (6marks)
- The displacement, S metres of a moving particle from point O, after t seconds is given by:
S = t3 – 5t2 + 3t + 10- Find S when t = 2 (2marks)
- When t = 2
S = (2)3 – 5(2)2 + 3(2) + 10
8 – 20 + 6 + 10
= 4m
- When t = 2
- Determine:
- The velocity of the particle when t = 5sec (3marks)
- V = ds/dt = 3t2 – 10t + 3
When t = 5
V = 3(5)2 – 10(5) + 3
75 – 50 + 3
= 28 m/s
- V = ds/dt = 3t2 – 10t + 3
- The value of t when the particles is momentarily at rest . (3 marks)
- Momentarily at rest V = 0
3t2 – 10t + 3 = 0
3t2 – 9t – t + 3 = 0
3t(t – 3) 1(t – 3) = 0
(3t – 1) (t – 3) = 0
Either
3t – 1 = 0 → t = 1/3sec
Or t – 3 = 0 → t = 3 sec
- Momentarily at rest V = 0
- The velocity of the particle when t = 5sec (3marks)
- Find the time, when the velocity of the particle is maximum. (2 marks)
Velocity maximum dvdt=0- 6t – 10 = 0
6t = 10
t = 106 =53 seconds
- 6t – 10 = 0
- Find S when t = 2 (2marks)
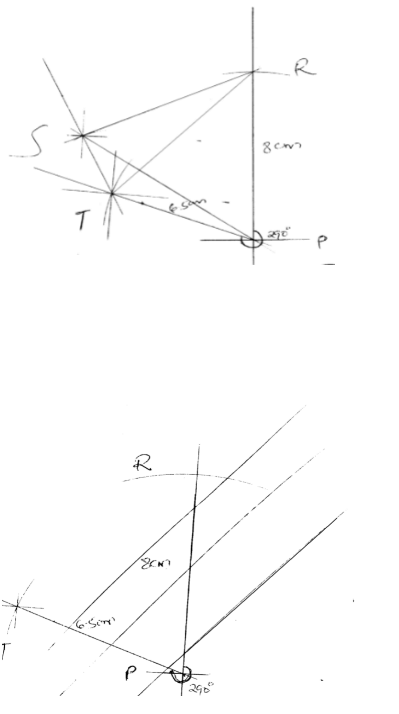
- Four towns P, R, T and S are such that R is 80km directly to the north of P and T is on a bearing of 290° from P at a distance of 65km. S is on a bearing of 330° from T and a distance of 30 km. Using a scale of 1cm to represent 10km, make an accurate scale drawing to show the relative position of the towns. (4mks)
Find:- The distance and the bearing of R from T (3mks)
84km, 0420 - The distance and the bearing of S from R (2mks)
80km, 0650 - The bearing of P from S (1mk)
120º
- The distance and the bearing of R from T (3mks)
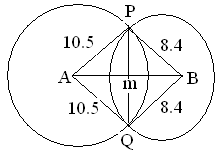
- The figure below shows two circles of radii 10.5 and 8.4cm and with centres A and B respectively. The common chord PQ 9cm.
- Calculate angle PAQ. (2 mks)
< PAQ = <PAM + <QAM
< PAM = sinθ1 =4.5/10.5=0.4286
Sin -1 (0.4286) = 25.38º
< QAM = <PAM = 25.38º
→<LAP = 25.38x2= 50.76º - Calculate angle PBQ. (2 mks)
<PBQ = < PBM + <QBM
< PBM = sin∝1 =45/84=0.5357
Sin-1 (0.5357) = 32.39º
< PBM = <QBM = 32.39º
<PBQ = 32.390x 2 = 64.78º - Calculate the area of the shaded part. (6 mks)
area of segment = area of a section – area of DTaking (i)
=
= 48.84 – 42.69 = 6.15cm2
Taking (ii)
=
= 39.89 – 31.92 = 7.97cm2
= (6.15 + 7.97) cm2 = 14.12cm2
- Calculate angle PAQ. (2 mks)
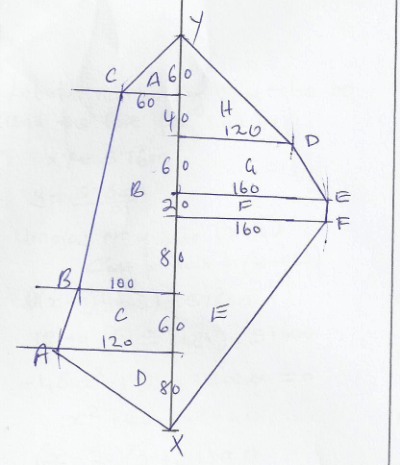
- The following measurement were recorded in a field book using XY as the baseline. XY = 400m.
Y C60 340 300 1200 240 160E 220 160F B100 140 A120 80 X - Using a scale of 1:4000 draw an accurate map of the farm. (4 marks)
- Determine the actual area of the farm in hectares. (4 marks)
- Area A = ½ x 60 x 60 = 1800
- B = ½ (60 + 100) x 200 = 2600
- C = ½ (100 + 120) x 60 = 6600
- D = ½ x 80 x 120 = 4800
- E = ½ x 160 x 200 = 16000
- F = 20 x 160 = 3200
- G = ½ (120 + 160x 60 = 8400
- H = ½ x 100 x 120 = 6000
=72800
= 72800 = 7.28 ha
1000
- If the farm is on sale at sh.80,000 per hectare find how much the farm costs.(2marks)
7.28 x 80,000 = sh.582400
- Using a scale of 1:4000 draw an accurate map of the farm. (4 marks)
- The length and breadth of a rectangle are given as (6x - 1) and (x -2) metres respectively. If the length and breadth are each increased by 4 metres, the new area is three times that of original rectangle.
- Form an equation in x and solve it. (4 marks)
- Dimensions of the new rectangle
(6x +3) and (x + 2)
(6x + 3) (x +2) = 6x2 + 15x + 6
= 6x2 + 15x +6 = 3 (6x - 1) (x- 2)
= 6x2 + 15x + 6 = 18x2 – 39x + 6
12x2 – 54x = 0
6x(2x -9) = 0
2x = 9 x =4.5
- Dimensions of the new rectangle
- Find the dimensions of the original triangle (2 marks)
- Length = 26m
Breadth = 2.5m
Original area
26 x 2.5 = 65m2
- Length = 26m
- Express the increase in area as a percentage of the original area. (4 marks)
- New area
30 x 6.5 = 195m2
% increase
= 195-6565×100%
= 200%
- New area
- Form an equation in x and solve it. (4 marks)
- X, Y and Z are three quantities such that X varies directly as the square of Y and inversely as the square root of Z.
- Given that X = 18 when Y = 3 and Z = 4, find X when Y = 6 and Z = 16. (5 marks)
- x r2/√z
x kr2/√zwhen r=3 and z=4, x=18
18= k32/√4=18=9/2k
therefore18 ×2/9 =4
EQN × kr2/√z
when r=6, and z=16= 4(6)2/√16=4 ×36/4
=36
- x r2/√z
- If Y increases by 10% and Z decreases by 19%, find the percentage increase in X. (5 marks)
let x1= xky12/√z1
r1110/100 r=1.1 r
z1 = 81/100z= 0.81z
% increase=(x1-x/x)100k(1.1r)2- ky2
√0.81z √z
ky2
√zky2(1.21-1)×100
√z 0.9
ky2√z
=310
9increase in x=34.44%
A. increase in x=34.44%
B 4.6 ±0.1 ×10=46 KM ±1 KM
C 240° ±1° OR S 60 ° W ±2°
D 122° ±OR S 58° E ±1°
E 127 ±0.1 ×10=127 ±1 KM
- Given that X = 18 when Y = 3 and Z = 4, find X when Y = 6 and Z = 16. (5 marks)
- The diagram below a circle, centre O. PQ is a tangent to the circle at Q and PTOR is a straight line. QRST is a cyclic quadrilateral in which angle RTS = 350 and RT and QS are diameters. Giving reasons for your answer, find the size of:
- Acute angle ROS. (2marks)
- Acute ∠ROS = 2∠RTS
(∠ at centre)
2 x 35 = 70º
- Acute ∠ROS = 2∠RTS
- Angle RQS. (2 marks)
- ∠RQS = ∠RTS
∠s in the same segment
= 35º
- ∠RQS = ∠RTS
- Angle PQR. (2 marks)
∠PQS = 90º (∠ made by a tangent and radius)
∠PQR = ∠PQS + ∠RQS
= 90º + 35º
= 125º - Angle QPT. (2 marks)
∠QOT = ∠ROS = 35º
(vertically opposite angles)
In ΔPOQ, ∠QPT = 180o – (90 – 70)º
= 20º (Sum of ∠s in a Δ) - Angle PQT. (2 marks)
- In ΔPQR, ∠PRQ = 180o – (125 + 20)º
= 35º (∠ sum of Δ)
∠PQT = ∠PRQ (∠s in alternate segment)
= 35º
- In ΔPQR, ∠PRQ = 180o – (125 + 20)º
- Acute angle ROS. (2marks)
Download Mathematics Paper 1 Questions and Answers - Form 4 End Term 1 Exams 2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students