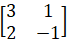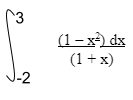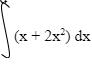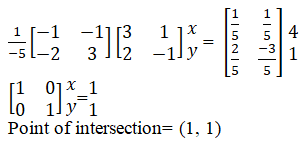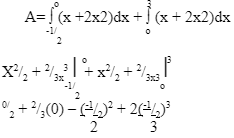Mathematics Paper 2 Questions and Answers - Form 4 End Term 1 Exams 2021

MATHEMATICS
FORM 4
END TERM EXAMS
TERM 1 2021
PAPER 2
TIME 2½ hrs

INSTRUCTIONS

This paper has two sections: Section I and II
Answer all questions in Section I and and FIVE in Section II

SECTION I (50MARKS)
Answer all the questions in this section in the spaces provided.

The length and width of a rectangular window pane measured to the nearest millimeter are 8.6cm and 5.3 respectively. Find to four significant figures, the percentage error in the area of the window pane. (3mks)(Answer to 4 significant figures)
Without using a calculator or mathematical tables, express in surd form and simplify leaving your answer in the form a + b √c where a, b and c are rational numbers. (3mks)
Cos 30º
Tan 45 + √3
In the figure below, O is the centre of the circle which passes through the points T,C and D. Line TC is parallel to OD and line ATB is a tangent to the circle at T. Angle DOC = 380. Calculate the size of angle CTB (3mks)
A coffee dealer mixes two brands of coffee, x and y, to obtain 40kg of the mixture worth Ksh. 65 per kg. If brand x is valued at Ksh. 70 per kg and brand y at ks.55 per kg. Calculate the ratio, in its simplest form, in which the brands x and y are mixed. (2mks)
Find the radius and the coordinate of the centre of the circle whose equation is
2x² + 2y² – 6x + 10y + 9 = 0 (3mks)
1. Expand (1 + ¼ x)⁴ (2mks)
2. Use your expansion in (a) above to evaluate (0.975)⁴ to 4 significant figures. (2mks)
When Ksh. 60,000 was invested in a certain bank for 8years it earned a simple interest of Ksh. 14,400. Find the amount that must have been invested in the same bank at the same rate for 5years to earn a simple interest of Ksh. 12,000 (3mks)
Given that P = 2q – r, express q in terms of p and r (3mks)
q + 3r
→ →
If OA = 3i + 2j – 4k and OB = 4i + 5j – 2k, P divides AB in the ratio 3:-2. Determine the modulus of OP leaving your answer to 1 decimal place. Given that O is the origin. (3mks)
Solve for x in 2 +log₇(3x-4) =log₇98 (3mks)
A carpenter wishes to make, a ladder with 18 cross-pieces. The cross pieces are to diminish uniformly in lengths from 65cm at the bottom to 31cm at the top. Calculate the length in cm, of the eighth cross-piece from the bottom. (3mks)
A quantity P varies partly as Q and partly as the square root of Q, given that P=30 when Q=9, and P=14 when Q=16. Find P when Q=36. (3mks)
Seven people can build five huts in 30 days. Find the number of people, working at the same rate that will build 9 similar huts in 27days. (3mks)
1. A and B are two points on earth’s surface and on latitude 400 N. The two points are on the longitude 500W and 1300E respectively. Calculate the distance from A to B along a parallel of latitude in kilometers. (2mks)
2. The shortest distance from A to B along a great circle in kilometres (Take π = 22/7 and radius of the earth = 6370km) (2mks)
Find the inverse of the matrix shown hence find the coordinates of the point Of intersection of the lines
3x + y = 4 and 2x – y = 1 (3mks)
Evaluate (4mks)

SECTION II
Answer any Five questions in this section

The following are marks scored by form four student in Mathematics test.

Marks 10-19 20-29 30-39 40-49 50-59 60-69 70-79 80-89 90-99

Frequency 2 6 10 16 24 20 12 8 2

Using an assumed mean of 54.5, calculate the
1. Mean mark (4mks)
2. Variance (4mks)
3. Standard deviation (2mks)
A bag contains 5 red, 4 white and 3 blue beads. Three beads are selected at random without replacement. Find the probability that
1. The first red bead is the third bead picked. (2mks)
2. The beads selected were, white and blue: (2mks)
  1. In that order
  2. In any order (2mks)
3. No red bead is picked (2mks)
4. Beads picked are of the same colour. (2mks)
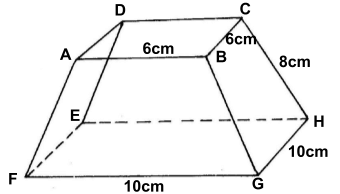
The figure below shows solid frustum of a pyramid with a square top of side 6cm and a square base of side 10cm. The slant edge of the frustum is 8cm.
1. Calculate the total surface area of the frustum (4mks)
2. Calculate the volume of the solid frustum. (3mks)
3. Calculate the angle between the planes BCHG and the base EFGH. (3mks)
1. Using a ruler and pair of compasses only construct triangle ABC in which AB = 6.5cm, BC= 5.0cm and angle ABC = 600. Measure AC (3mks)
2. On same side of AB as C (3mks)
  1. Determine the locus of a point P such that angle APB = 600 (3mks)
  2. Construct the locus of R such that AR = 3cm. (1mk)
  3. Identify the region T such that AR ≥ 3 and ∠APB ≥ 600 by shading the unwanted part. (3mks)
The table below shows income tax rates

Monthly income Tax Rate

(Kshs) (%)

Up to 9680 10

9681 – 18800 15

18801-27920 20

27921-37040 25

37041 and above 30

Omari’s monthly taxable income is Ksh. 24200
1. Calculate the tax charged on Omari’s monthly earnings. (4mks)
2. Omari is entitled to the following tax relief of 15% of the premium paid.
  Calculate the tax Omari pays each month if he pays a monthly insurance premium of Ksh. 2400 (2mks)
3. During a certain month, Omari received additional earnings which were taxed at 20% each shilling. Given that he paid 36.3% more tax that month, calculate the percentage increase in his earning. (4mks)
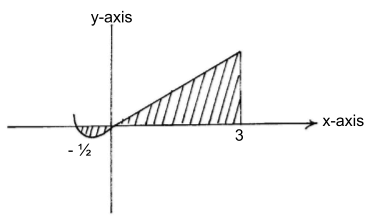
The curve of the equation y = x+ 2x2, has x = ½ and x = 0 as x-intercepts. The area bounded by the x-axis, x = ½ and x = 3 is shown by the sketch below.

Find
2. The exact area bounded by the curve, x axis (7mks)
  x= -½ and x=3 (Give your answer to 2dp)
1. Fill in the table below to 2 decimal places for the graph of y = sin x and y = 2sin (x-30) for the range
  – 180 ≤ x ≤180 (2mks)
  
  xº -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180
  
  Sin xº 0 -1.0 -0.87 0 0.87 0.5
  
  2 Sin (x – 30)º 1 -1.73 -2.0 -1 1.0 1.73
2. On a graph, using a scale of 1cm to represent 300 on the x-axis and 1cm to represent 0.5 units on the y-axis, draw the graph of y= Sin x0 and y = 2 sin(x – 30)0 on the same axes (4mks)
3. Using your graph
  1. State the amplitude and the period of the graph y = 2 sin (x-30)0 (1mk)
  2. Solve the equation
    Sin xº = 2 sin (x-30)º (1mk)
  3. Describe fully the transformation that will map y = 2sin (x-30)0 on y = sin x (2mks)
A tailor makes two types of garments A and B. Garment A requires 3 metres of material while garment B requires 2 ½ metres of material. The tailor uses not more than 600 metres of material daily in making both garments. He must make not more than 100 garments of type A and not less than 80 of type B each day.
1. Write down all the inequalities from this information. (3mks)
2. Graph the inequalities in (a) above (3mks)
3. If the business makes a profit of shs. 80 on garment A and a profit of shs. 60 on garment B, how many garments of each type must it make in order to maximize the total profit? (4mks)

MARKING SCHEME

SECTION I (50MARKS)
Answer all the questions in this section in the spaces provided.

The length and width of a rectangular window pane measured to the nearest millimeter are 8.6cm and 5.3 respectively. Find to four significant figures, the percentage error in the area of the window pane. (3mks)(Answer to 4 significant figures)
- Maximum area ⇒ 8.65 x 5.35 = 46.2775
  Actual area ⇒ 8.6 x 5.3 = 45.58
  Minimum area ⇒ 8.55 x 5.25 = 44.8875
  Absolute error = 46.2275 – 44.8875
  2
  % error = 0.695 x 100%
  45.58
  = 1.525%
Without using a calculator or mathematical tables, express in surd form and simplify leaving your answer in the form a + b √c where a, b and c are rational numbers. (3mks)
Cos 30º
Tan 45 + √3
√ 3/2
1 +√ 3
√ 3 = √ 3(2-2√ 3)
2 + 2√ 3 (2 + 2 √3 ) (2-2√3)
-2/8√3 + 3/4
= ³/₄ – ¹/₄ √3
In the figure below, O is the centre of the circle which passes through the points T,C and D. Line TC is parallel to OD and line ATB is a tangent to the circle at T. Angle DOC = 380. Calculate the size of angle CTB (3mks)

< OCT = 38º
< TOC = 102º
< CTB = 51º
A coffee dealer mixes two brands of coffee, x and y, to obtain 40kg of the mixture worth Ksh. 65 per kg. If brand x is valued at Ksh. 70 per kg and brand y at ks.55 per kg. Calculate the ratio, in its simplest form, in which the brands x and y are mixed. (2mks)
70x + 55y = 65(x +y)
5x = 10y
x : y = 2:1
Find the radius and the coordinate of the centre of the circle whose equation is
2x² + 2y² – 6x + 10y + 9 = 0 (3mks)

(x – ³/₂)² + (y +⁵/₂)² = ¹⁶/₄Center = (9,t) = (3/2 – 5/2) = (1.5, -2.5)
r = √ 16/4 = 2
Or
x² + y² – 3x + 5y + ⁹/₂ = 0
x² + y² + 29x + 2fy + c = 0
-2g = -3 -2f = 5
G = ³/₂ f =^-5/₂Radius r =√ (f² + g² - c) = ²⁵/₄ + ⁹/₄ – ⁹/₂r = √ 16/4 = 2
1. Expand (1 + ¼ x)⁴ (2mks)
  - (1⁴ + 4x ¹/₄x) + 6 (¹/_4x)² + 4(¹/_4x)³ + (¹/_4x)⁴1 + ¹/_x + ³/_8x² + ¹/_6x³ + ¹/_6x⁴
2. Use your expansion in (a) above to evaluate (0.975)⁴ to 4 significant figures. (2mks)
  - 1 + ¹/_-10 + ³/_8(-10)² + ¹/_16(-10)³ + ¹/_64(-10)⁴
  - = 0.903689063
    = 0.9037
When Ksh. 60,000 was invested in a certain bank for 8years it earned a simple interest of Ksh. 14,400. Find the amount that must have been invested in the same bank at the same rate for 5years to earn a simple interest of Ksh. 12,000 (3mks)
- 60000 x 8xt = 14400
  100
  T = 3 years.
  P x 5 x 3 = 12000
  100
  P = 80,000
Given that P = 2q – r, express q in terms of p and r (3mks)
q + 3r
- p(q + 3r) = 2q – r
  pq + 3pr = 2q – r
  pq -2q = -r – 3pr
  q(p-2)=-r-3pr
  q=-r-3pr
  p-2
  
  → →
If OA = 3i + 2j – 4k and OB = 4i + 5j – 2k, P divides AB in the ratio 3:-2. Determine the modulus of OP leaving your answer to 1 decimal place. Given that O is the origin. (3mks)
Let p be point (x, y, z)
x 3 4
1/3 y + 2/3 2 = 5
Z -4 -2
P(6,11,2)
10p1 = √ (6)2 + (11)2 + (2)2
= √ 161 = 12.69 units
Solve for x in 2 +log₇(3x-4) =log₇98 (3mks)
- Log₇2 + log₇ (3x-4) = log₇ 98
  49 (x - 4) = 98
  3x – 4 = 2
  3x = 6
  X = 2
A carpenter wishes to make, a ladder with 18 cross-pieces. The cross pieces are to diminish uniformly in lengths from 65cm at the bottom to 31cm at the top. Calculate the length in cm, of the eighth cross-piece from the bottom. (3mks)
31 = 65 + 17d ⇒ 17d = -34
d = -2
T8 = 65 + 7(-2)
= 65 – 14
= 51
A quantity P varies partly as Q and partly as the square root of Q, given that P=30 when Q=9, and P=14 when Q=16. Find P when Q=36. (3mks)
- Let L and K be constants.
  P=LQ + K √Q
  30 = 9L + √9K
  14 = 162 + √16 K
  2K + 62 = 20
  2K + 8L = 7
  -2L = 13
  L = ^-13/₂K + 3(^-13/₂) = 10
  K = ¹⁰/₁ + 392 = ⁵⁹/₂P = ^-13/₂Q = ⁵⁹/₂ √Q
  P = ^-13/₂ x 36 + ⁵⁹/₂ x √36
  P = -234 + 177 = -57
Seven people can build five huts in 30 days. Find the number of people, working at the same rate that will build 9 similar huts in 27days. (3mks)
People Huts days
7 5 30
9 27
7 x ³⁰/₂₇ x ⁹/₅= 14 people
1. A and B are two points on earth’s surface and on latitude 400 N. The two points are on the longitude 500W and 1300E respectively. Calculate the distance from A to B along a parallel of latitude in kilometers. (2mks)
  - d =¹⁸⁰/₃₆₀ x 2 x 6370 x ²²/₇ Cos 40º
    = ¹/₂ x ²²/₇ x 2 4879.7
    = 15336.2 km
2. The shortest distance from A to B along a great circle in kilometres (Take π = 22/7 and radius of the earth = 6370km) (2mks)
  - ¹⁰⁰/₃₆₀ x 2 6370 x 22/7
    = 11122.2
Find the inverse of the matrix shown hence find the coordinates of the point Of intersection of the lines
3x + y = 4 and 2x – y = 1 (3mks)

Determinant
(3 x-1)-(2x1)=(-3-2)=-5
-¹/₅
Evaluate (4mks)

(1-x)(1 +x) = 1 – x
1 + x
³
∫ (1-x)dx
_-2
x – x²/2 + c
3 - 3² /2 + c – 2 – (-2)² + c
= 3 – 4.5 + c - -2 + 2 + c
-1.5 + c – c
= -1.5

SECTION II
Answer any Five questions in this section

The following are marks scored by form four student in Mathematics test.

Marks	10-19	20-29	30-39	40-49	50-59	60-69	70-79	80-89	90-99
Frequency	2	6	10	16	24	20	12	8	2

Using an assumed mean of 54.5, calculate the

Mean mark (4mks)

Marks	Mp(x)	d(x-a)	Fd	D²	Fd²
10-19	2	14.5	-40	-80	1600	3200
20-29	6	24.5	-30	-180	900	5400
30-39	10	34.5	-20	-200	400	4000
40-49	16	44.5	-10	-160	100	1600
50-59	24	54.5	0	0	0	0
60-69	20	64.5	10	200	100	200
70-79	12	74.5	20	240	400	4800
80-89	8	84.5	30	240	900	7200
90-99	2	94.5	40	80	1600	3200
				140		31400

Mean = A + Σfd
Σf
= 54.5 + 140/100 = 55.9

Variance (4mks)
- Variance= 31400/100 – (140/100)²
  = 312.04
Standard deviation (2mks)
- standard varaitaion = √variance
  √ 312.04 = 17.06

A bag contains 5 red, 4 white and 3 blue beads. Three beads are selected at random without replacement. Find the probability that
1. The first red bead is the third bead picked. (2mks)
  - P(WWR or WBR or BBR or BWR)
    (⁴/₁₂ X ³/₁₁ X ⁵/₁₀) + ⁴/₁₂ X ³/₁₁ X ⁵/₁₀
    + (³/₁₂ x ²/₁₁ x ⁵/₁₀ + (³/₁₂ x ⁴/₁₁ x ⁵/₁₀))
    =²/₁₁
2. The beads selected were, white and blue: (2mks)
  1. In that order
    ⁵/₁₂ x ⁴/₁₁ x ³/₁₀ = ¹/₂₂
  2. In any order (2mks)
    - P(RWB or RBW or WBR or WRB or BWR or BRW)
      (⁵/₁₂ x ⁴/₁₁ x ³/₁₀) + (⁵/₁₂ x ³/₁₁ X ⁴/₁₀)
      + (⁴/₁₂ x ³/₁₁ x ⁵/₁₀)
      = ⁶/₅₂ = ³/₁₁
3. No red bead is picked (2mks)
  - P(BBB or BBW or BWB or BWW or WWW or WWB or WBW OR WBB)
    (³/₁₂ x ²/₁₁ x ¹/₁₀)+(³/₁₂x²/₁₁x⁴/₁₀)+(³/₁₂x⁴/₁₁x²/₁₀)+(³/₁₂x⁴/₁₁x³/₁₀ )+
    (⁴/₁₂x³/₁₁x²/₁₀)+(⁴/₁₂x³/₁₁x³/₁₀) +(⁴/₁₂x³/₁₁x²/₁₀)
    =⁷/₄₄
4. Beads picked are of the same colour. (2mks)
  - P(BBB or WWW or RRR)
    (³/₁₂x²/₁₁x¹/₁₀)+(⁴/₁₂x³/₁₁x²/₁₀)+(⁵/₁₂ x ⁴/₁₁x³/₁₀)
    = ¹/₂₂₀ + ¹/₅₅ + ¹/₅₅ = ⁹/₂₂₀
The figure below shows solid frustum of a pyramid with a square top of side 6cm and a square base of side 10cm. The slant edge of the frustum is 8cm.
1. Calculate the total surface area of the frustum (4mks)
  - ⁶/₁₀ =^l/_{8 +L}
    12 = L
    Base area = 102 = 100
    Area of 4Δs = 4√25(25-20)(25-20)(25-20)
    = 4√25 x 5 x 5x 15
    = 4√ 9375
    T.S.A of the pyramid = 100 + 387.28
    = 487.28cm²
    Area of the slanting edges of thr small pyramid
    = 4√15(3)(3)(9)
    = 139.44
    Surface of the solid frustrum
    = 487 .28 +36-139.44
    383.84
2. Calculate the volume of the solid frustum. (3mks)
  - Volume = 1/3 x 100 x 18.71
    = 62.61
    L.S.F = 3/5 ⇒ V.S.F 27/125
    Fraction representing Frustrum
    = 98/125
    ∴Volume of the frustrum = 98/125 x 623.61
    = 488.91
3. Calculate the angle between the planes BCHG and the base EFGH. (3mks)
  - tanα=18.71
    5
    α = 75.03º
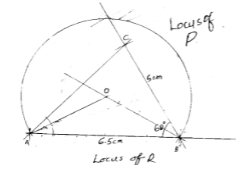
1. Using a ruler and pair of compasses only construct triangle ABC in which AB = 6.5cm, BC= 5.0cm and angle ABC = 600. Measure AC (3mks)
  
  AC=5.8±1
2. On same side of AB as C (3mks)
  1. Determine the locus of a point P such that angle APB = 60º (3mks)
  2. Construct the locus of R such that AR = 3cm. (1mk)
  3. Identify the region T such that AR ≥ 3 and ∠APB ≥ 60º by shading the unwanted part. (3mks)
The table below shows income tax rates

Monthly income Tax Rate

(Kshs) (%)

Up to 9680 10

9681 – 18800 15

18801-27920 20

27921-37040 25

37041 and above 30

Omari’s monthly taxable income is Ksh. 24200
1. Calculate the tax charged on Omari’s monthly earnings. (4mks)
  Tax on 1st ksh 9680 = 9680 x 10/100 = kshs. 968
  Tax on 2nd kshs. 9120 = 9120 x 15/100= kshs 1368
  Tax on rem kshs. 5400 = 5400 x 20/100= ksh 1080
  Total tax = 968 + 1368 + 1080 = kshs. 3416
2. Omari is entitled to the following tax relief of 15% of the premium paid.
  Calculate the tax Omari pays each month if he pays a monthly insurance premium of Ksh. 2400 (2mks)
  - Tax paid= 3416-(1056 + 2400 x 15/100)
    = kshs. 2000
3. During a certain month, Omari received additional earnings which were taxed at 20% each shilling. Given that he paid 36.3% more tax that month, calculate the percentage increase in his earning. (4mks)
  - Increase in tax paid = 2000 x 36.3= kshs. 726
    Increase in earnings= kshs. 726 x 100/20= ksh. 3630
    % increase = 3630 x 100
    24200
The curve of the equation y = x+ 2x2, has x = ½ and x = 0 as x-intercepts. The area bounded by the x-axis, x = ½ and x = 3 is shown by the sketch below.

Find
1. x²/2 + 2/3x3 + c
2. The exact area bounded by the curve, x axis (7mks)
  x= -½ and x=3 (Give your answer to 2dp)
  
  =0-(¹/₈ – ¹/₁₂)
  = - (3-2)
  24
  = - ¹/₂₄ ∴ ¹/₂₄
  ^₃2/₂ + ²/₃ x 33 __(0)
  
  9/2 + 54/3
  4.5 + 18 = 22.5
  Total area = ¹/₂₄ + 22.5=0.0416 + 22.5
  = 22.54

Fill in the table below to 2 decimal places for the graph of y = sin x and y = 2sin (x-30) for the range
– 180 ≤ x ≤180 (2mks)

xº	-180	-150	-120	-90	-60	-30	0	30	60	90	120	150	180
Sin xº	0	-0.5	-0.87	-1.0	-0.87	-0.5	0	0.5	0.87	1.0	0.87	0.5	0.0
2 Sin (x – 30)º	1	0	-1.0	-1.73	-2.0	0	-1	0	1.0	1.73	2.0	1.73	1.0

On a graph, using a scale of 1cm to represent 300 on the x-axis and 1cm to represent 0.5 units on the y-axis, draw the graph of y= Sin x0 and y = 2 sin(x – 30)0 on the same axes (4mks)
Using your graph
1. State the amplitude and the period of the graph y = 2 sin (x-30)0 (1mk)
  - y = 2sin(x- 30º)
    Amplitude = 3units
    Period = 360º
2. Solve the equation
  Sin xº = 2 sin (x-30)º (1mk)
  SinX = 2Sin (x – 30º)
  X = -126º cr 51.50 ±1º
3. Describe fully the transformation that will map y = 2sin (x-30)0 on y = sin x (2mks)
  +30
  0 Translation

A tailor makes two types of garments A and B. Garment A requires 3 metres of material while garment B requires 2 ½ metres of material. The tailor uses not more than 600 metres of material daily in making both garments. He must make not more than 100 garments of type A and not less than 80 of type B each day.
1. Write down all the inequalities from this information. (3mks)
  (i) 3x + 2 1/2y ≤ 600
  (ii) x ≤ 100
  (iii) Y ≥ 80, x ≥ 0
2. Graph the inequalities in (a) above (3mks)
  
  line 3x + 2 1/2y ≤ 600
  Line x ≤ 100
  Line ≥ 80, x ≥ 0
3. If the business makes a profit of shs. 80 on garment A and a profit of shs. 60 on garment B, how many garments of each type must it make in order to maximize the total profit? (4mks)
  The objective functions
  P = 80x + 60y
  100 garments of type A
  120 garments of type B