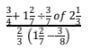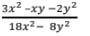Mathematics Paper 1 Questions and Answers - Form 4 Mid Term 2 Exams 2021

MATHEMATICS
PAPER 1
FORM 4 MID TERM 2

INSTRUCTIONS

• This paper consists of two Sections; Section I and Section II.
• Answer ALL the questions in Section I and any five questions from Section II.
• Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I: (50 MARKS)
Answer all the question in this section in the spaces provided.

1. Without using a calculator , evaluate:(3 mks)
   
2. Simplify completely. (3 mks)
   
3. The price of an article is marked as 12,000/= Mr. Omanga sold the article at a discount of 10% and still made a profit of 8%. Calculate the cost of the article. (3 mks)
4. Three sirens wail at intervals of thirty minutes, fifty minutes and sixty minutes. If they wail together at 7.18 a.m. on Monday, what time and day will they wail together? (3 mks)
5. The table shows the frequency distribution of marks scored by students in a test.
       Marks         Frequency
       21 - 30          2
       31 - 40          4
       41 - 50          11
       51 - 60          5
       61 - 70          3
   Determine the median mark correct to one decimal point. (3 mks)
6. A cylindrical solid whose radius and height are equal, has a total surface area of 154cm². Calculate the diameter. (3mks).
7. The exterior angle of a regular polygon is (λ - 50)º and the interior angle is (2λ + 20)º. Find the number of sides of the polygon. (3 mks)
8. Solve the following inequalities and represent it on the number line. 6x + 2 < 3x + 11 ≤ 27x − 1 Write down the integral values that satisfy the inequality. (3mks)
9. Find the equation of a line through the point (2, 1), perpendicular to the line ¹/₂x + 2y = −3 (3 mks )
10. Find the value of x given that; 9^x + 2 × 3^2x − 243 = 0 (3mks).
11. The position vectors of A and B are given as OA = 2i – 3j + 4k and OB= -2i – j + 2k respectively. Find to 2 decimal places, the length of vector AB. (4 mks)
12. Use the exchange rates below to answer the question.
    

    	Buying	Selling
    1 us Dollar	63.00	63.50
    1 Euro	125.30	125.43

    A tourist arriving in Kenya from Britain has 9600 Euros. He converts the Euros to Kenya shillings at a commission of 5%, while in Kenya he converts the money to US dollars. If he was not charged any commission from the last transaction, calculate to the nearest USA dollar what he received. (3mks).
13. Given that sin(2x − 10)^o = cos 60^o and x is an acute angle, find x. (3 mks)
14. The length of a rectangle is (3x+1)cm. Its width is 3cm shorter than the length. Given that area of the rectangle is 28cm² , find its length. (3 mks)
15. The mass of two similar solid are 324g and 768g. Find
    1. height of the smaller solid if the height of the bigger solid is 20cm. (2 mks)
    2. the surface area of the smaller solid if the surface area of the bigger solid is 40cm².(2 mks)
16. The cost of three pens and five books is sh. 130. Kanyoro bought 2 of the pens and 3 of the books at sh. 80. How much did he pay for each? (3mks)

SECTION II (50mks)
Answer only five questions in this section in the spaces provided.

17. A bus left Nairobi at 7a.m and travelled towards Eldoret at an average speed of 80km/h. At 7:45 a.m a car left Eldoret towards Nairobi at an average speed of 120 km/h. Given that the distance between Nairobi and Eldoret is 300km,
    Calculate:
    1. The time the bus arrived at Eldoret. (2 mks)
    2. The time of the day, the two met. (3 mks)
    3.  The distance from Nairobi to where the two met. (2 mks)
    4. The distance of the bus from Eldoret when the car arrived in Nairobi. (3 mks)
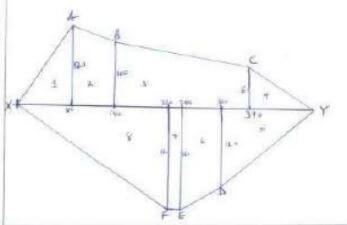
18. The following measurements were recorded in a field book using XY as the base line. XY = 400m.
              Y
    C 60  340
             300 120 D
             240 160 E
             220 160 F
    B 100 140
    A 120 80
               X
    1. Using a scale of 1: 4000, draw an accurate map of the farm. (4 mks)
    2. Determine the actual area of the farm in hectares. (4 mks)
    3. If the farm is on sale at sh.80,000 per hectare, find how much the farm costs.(2 mks)
19. Mr. Omwega is employed. His basic salary is Kshs. 21, 750 and is entitled to a house allowance of Kshs 15, 000 and a travelling allowance of Kshs 8, 000 per month. He also claims a personal monthly relief of Kshs 1, 056 per month. Other deductions are; Union dues Kshs 200 and Co-operative shares Kshs 4, 500 per month. The table below shows the tax rates for the year.
    

    Income (Kshs per annum)	Tax rates
    1 – 116, 600 116, 161 – 225, 600 225, 601 – 335, 040 335, 041 – 444, 480 Over 444, 480	10% 15% 20% 25% 30%

    Calculate;
    1. Mr. Omwega’s annual taxable income. (2 mks)
    2. The tax paid by Mr. Omwega in the year. (6 mks)
    3. Mr. Omwega’s net income per month. (2 mks)
20. A straight line L₁ has a gradient ^-1/₂ and passes through point P (-1, 3). Another line L₂ passes through the points Q (1, -3) and R (4, 5). Find.
    1. The equation of L₁. (2 mks)
    2. The gradient of L₂. (1 mk)
    3. The equation of L₂. (2 mks)
    4. The equation of a line passing through a point S (0, 5) and is perpendicular to L₂ (3 mks)
    5. The equation of a line through R parallel to L₁. (2 mks)
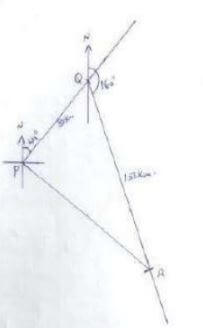
21. A ship leaves port P and sails to port Q which is 80km away on a bearing of 040^o. The ship then sails from Q to R on a bearing 160^o where R is 150km from Q. From R, the ship returns directly to P at a speed of 25km/h.
    1. Using a suitable scale show the relative positions of P, Q and R. (3 mks)
    2. Find the bearing of R from P (2 mks)
    3. Find the distance travelled from R and the time taken to arrive at the destination(3 mks)
    4. An island S is equidistant from P, Q and R. Show its relative position. (2 mks)
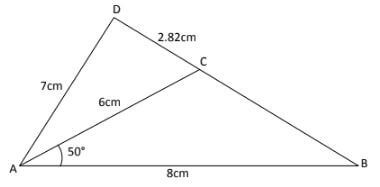
22. In the figure below (not drawn to scale) AB = 8cm, AC = 6cm, AD = 7cm, CD = 2.82cm and angle CAB = 50°.
    
    Calculate (to 2d.p.)
    1. The length BC. (3 mks)
    2. The size of angle ABC. (3 mks)
    3. Size of angle CAD. (2 mks)
    4. Calculate the area of triangle ACD. (2 mks)
23.         
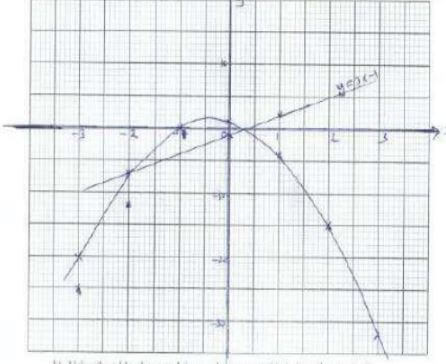
    1. Complete the table for the function y = 1 – 2x - 3x² in the range -3 ≤ x ≤ 3 (2 mks)
       

       X	-3	-2	-1	0	1	2	3
       -3x2	-27		-3	0		-12
       -2x		4		0			-6
       1	1	1	1	1	1	1	1
       Y	-20					-15

    2. Using the table above and the graph paper provided, draw the graph of y = 1 – 2x –3x² (4 mks)
    3. Use the graph in (b) above to solve
       1. 1 – 2x – 3x² = 0 (2 mks)
       2. 2 – 5x – 3x² = 0 (2 mks)
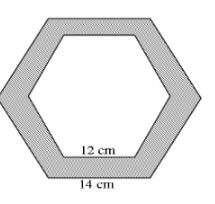
24. The diagram below (not drawn to scale) shows the cross – section of a hexagonal solid metal prism length 20cm.
    
    Calculate;
    1. The area of the shaded region (Take hexagon to be regular). (5 mks)
    2. The volume of the material used to make the metal in cm³(2 mks)
    3. If the density of the metal prism is 3.5 g/ cm³, find its mass in kg. (3 mks)

MARKING SCHEME

1. Numerator
   ³/₄ + ⁹/₇ ÷ ³/₇ x ⁷/₃
   ³/₄ + ⁹/₇ x 1
   ³/₄ + ⁹/₇ = ^{21 + 27}/₂₈
   ⁴⁸/₂₈
   ¹²/₇
   Denominator
   ²/₃(⁹/₇ - ³/₈)
   =²/₃(^72-21/₅₆)
   ²/₃ x ⁵¹/₅₆
   ¹⁷/₂₈
   Num/Den = ¹²/₇ ÷ ¹²/₂₈ = ¹²/₇ x ²⁸/₁₇
   2¹⁴/₁₇
   
   
2. Numerator
   3x2-xy-xy2
   3x2-3xy+2xy-2y2
   3x(x-y)+2y(x-y)
   (3x+2y)(x-y)
   Denominator
   2(9x2-4y2)=2(3x+2y)(3x-xy)
     (3x+2y)(x-y)      =  x-y   
   2(3x+xy)(3x-xy)      6x-4y
   
   
3. Sh 12000 → 100%
   S.P → 90%
   SP=^1200x90/₁₀₀=10,800
   Sh10 → 108%
   B.P → 100%
   B.P = ^{10800 x 100}/₁₀₈ = sh10,000
   
   
4.    LCM
   

   2	30	50	60
   2	15	25	30
   3	15	25	15
   5	5	25	5
   5	1	5	1

   LCM= 22x3x52
   =300min
   Time in hrs=³⁰⁰/₆₀=5hrs
   7:18am
   5:00
   12:18pm
   
   
5. 
   

   Close limit	f	c.f
   24.5 - 30.5 30.5 - 40.5 40.5 - 50.5 50.5 - 60.5 60.5 - 70.5	2 4 11 5 3	2 6 17 22 25

   Position:
   ²⁵/₂=12.5
   Median=
   40.5 + (^{12.5 -6}/₁₁)x10
   40.5 + (^{6.5 x 10}/₁₁)
   40.5 + 5.91
   =46.4
   
   
6. r=h
   2πr² + 2πrh = 154cm²
   2πr² + 2πr(r)=154
   4πr²=154
   4(²²/₇)r²=154
   r=√^154x7/₈₈ = 3.5cm
   distance=2 x 3.5=7cm
   
   
7. (x-50)+(2x+20)=180º
   3x-60=180º
   3x=210º
   x=70º
   Exterior angle= 70-50=20
   Number of sides= 360/20=18sides
   =18sides
   
   
8. 6x+2<3x+11
   3x<9
   x<3
   3x+11<27x-1
   ^-24/₂₄x <^-12/₂₄
   x>¹/₂
   ¹/₂<x<3
   
   
9. 1/2x+2y=-3
   2y=-1/2x-3
   y=-1/4x-3/2
   gradient(m)=-1/4
   M1xM2=-1
   -1/4 x M2= -1 → M2=4
   Equation of perpendicular
   y-1/r-2=4
   y-1=4x-8
   y=4x-7
   
   
10. 9x+2r32x=243
    32x+2x32x=243
    Let 32x=y
    y+2y=243
    3y=243
    y=81
    32x=34
    2x=4
    x=2
       
11.     
    
    Length of AB=√(-42)+22+(-2)2
    √24
    =4.90units
    
    
12.   Amount in Ksh= 9600 x 125.3= 1,202,880
    Amount ofter commission= 1,202,880 x ⁹⁵/₁₀₀= 1,142,736
    Amount in US$=1,142736/63.5 = 17,996
    
    
13. (2x-10)+ 60º=90º
    2x+50=90
    2x=40º
    x=20º
    
    
14.    
    (3x-2)(3x+1)=28
    9x²+3x-6x-2=28
    9x²-3x-30=0
    3x²-x-10=0
    3x²-6x+5x-10=0
    3x(x-2)+(5(x-2)=0
    (3x+5)(x-2)=0
    Either:
    3x+5=0 → x=-5/3
    OR
    x-2= → x=2
    Length = 3(x)+1=7cm
    
    
15.     
    1. vsf = ratio of mass = 324/768
       vsf=27/64
       lsf=³√²⁷/₆₄
       =³/₄
       ^h/₂₀=³/₄ → h=20x³/₄
       =15     
    2. a.s.f = (lsf)2
       (3/4)2
       =9/16
       A/40 = 9/16 → h=40 x 9/16
       =22.5cm2
       
       
16.    
    3ρ+5b=130
    2ρ+3b=80
    
    6ρ+10b=260
    6ρ+ 9b=240
            1b=20
    3ρ+5(2x)=130
    3ρ=30
    ρ=10
    1 pen=10KSh
    1 bok=20Ksh
       
17.     
    1. Time=d/s
       300km/80km/hr
       =33/4
       time of arrival 
        7:00am
        3:45   
       10:45am
       
       
    2. Distance travelled by bus for 46mins
       D=sxt
       80 x 3/4=60km
       Remaining dist=300-60=240km
       Rel Spd= 80+120=200km/hr
       Time taken= 240/200= 1hr 12 mins
       Time met
       7:45
       1:12
       9:57
       
       
    3. Distance travelled by cra when meeting:
       D= sxt
       120km/h x 1¹/₅=144km
       Dist from nai= 300-144=156km
       
       
    4. Time taken to nai by car:
       t= 300km/120km/hr= 2hrs 30 min
       7:45
       2:30
       10:15am
       Remaining dist= 80 x 1/2
       =40km   
18.     
    
    1.    
       
    2.    
       Area 1 = ½ x 80 x 120=4800m² 
       Area 2 = ½x 60 x (120+100)=6600m²
       Area 3 = ½ x 200x(100+60)=1600m²
       Area 4 = ½ x 60 x 60 = 1800m²
       Area 5 = ½ x 100 x 120 = 6000m²
       Area 6 = ½ x 60 x (160+12m²
       Area 8 = ½ x 160 x 220 = 17600m²
       Total area = 64400m²
       Area in ha= 64400/10,000=6.44ha
       
       
    3. Total cost= 6.44ha x 80,000= 515,200
19.      
    1. Month taxable income = 21750 + 15000 + 8000= 44750
       annua taxable inc= 44750x12=537,000
    2.    
       116600 x ¹⁰/₁₀₀ = 11660  
       109000 x  ¹⁵/₁₀₀= 16350
       109440 x  ²⁰/₁₀₀= 21888
       109440 x   ²⁵/₁₀₀= 27360
       92520 x ³⁰/₁₀₀ = 27756
       Total tax payable = 105014
       Tax due = tax payable - reliefs
       105014-(1056 x 12)
       105014- 12672
       =92342
       
       
    3. Tax p.m = 92342/12= 7695.17
       Net income= gross income - all deductions
       44750-12395.17= 32354.83/=
20.     
    1. ^y-3/_x-(-1)= -¹/₂
       2y-6= -x-1
       2y= -x+5
       y= ^-1/₂x+ ⁵/₂
       (any form of this eqn is acceptable)
       
       
    2.   Gradient of L₂= ^5-(-3)/_4-1
       =⁸/₃
       
       
    3. Eqn of L₂
       ^y-(-3)/_x-1=⁸/₃
       3y+9=8x-8
       3y=8x-17
       y= ⁸/₃x - ¹⁷/₃
       
       
    4.    
       1. M₁ x ⁸/₃=-1
          M=^-3/₈
          ^y-5/_x = -³/₈
          8y-40 = -3x
          8y=-3x+40
          y=-³/₈x+5
          
          
       2.  y-5/x-4 = -1/2
          2y-10= -x+4
          2y= -x+14
          y=-1/2x+7
21.      
    1.    
       
    2.   Distance PR=6.5x20
       130 ± 1km
       
       
    3. t=d/s
       ¹²⁰/₂₅
       =5hr 12 min 
       
       
    4. S is the centre of the circumference
22.      
    1. a²= b²+c²-2bcCosA
       a²=6²+8²-2(6)(8)Cos50º
       a²=100-61.71
       a=√38.29
       =6.19cm
       
       
    2. ^b/_{sin Bº} = ^a/_{Sin Aº}
       ⁶/_{Sin B}= ^6.19/ _{Sin 50º}
       Sin Aº= 6 x ^Sin50º/_6.19
       B= Sin^-10.7425
       =47.95º
       
       
    3. a2= 7²+6²-2(7)(6)CosA
       2.82²=85-84CosA
       Cos A= 85-2.82²
                      84
       A=Cos-10.9172
       =23.48º
       
       
    4. Area of ΔACD= ¹/₂ x 6 x 7 x Sin23.48
       =8.37cm²
23.      
    1.       
       

       X	-3	-2	-1	0	1	2	3
       -3x2	-27	-12	-3	0	-3	-12	-27
       -2x	6	4	2	0	-2	-4	-6
       1	1	1	1	1	1	1	1
       Y	-20	-7	0	1	-4	-15	-32

       
       
       
    2.    
       
    3.     
       1. Roots
          x=-1 or x=0.2
       2.   
          y=1-2x-3x2
          0=2x-5x-3x
          y=-1+3x
          Roots 
          x=-2 or x=0.3
24.     
    1. Area of Shaded R= (1/2 x 14x Sin 60)-(1/2x12xSin60)
       84.87-62.35
       =22.52
       Total area shaded R=22.5x6=135.12cm²
       
       
    2.  Volume= Area of cross-section length
       = 135.12cm² x 20cm
       =2702.4cm²
       
       
    3. Mass= density x volume
       3.5g/cm2 x 2702.4cm3
       9458.4g
       9.458kg