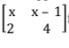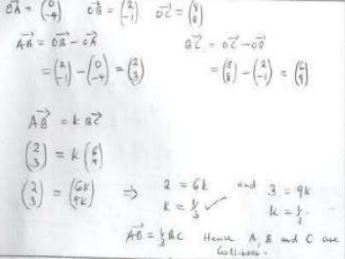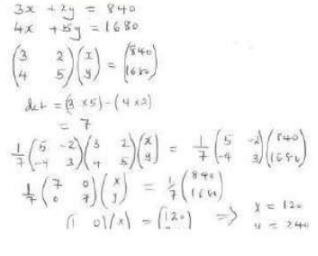Mathematics Paper 2 Questions and Answers - Form 4 Mid Term 2 Exams 2021

MATHEMATICS
PAPER 2
FORM 4 MID TERM 2

INSTRUCTIONS

• This paper consists of two Sections; Section I and Section II.
• Answer ALL the questions in Section I and any five questions from Section II.
• Show all the steps in your calculation, giving your answer at each stage in the spaces provided below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I: (50 MARKS)
Answer all the question in this section in the spaces provided.

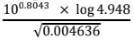
1. Use logarithm tables only correct 4 d.p to evaluate: (4 mks)
   
2. Find the centre and radius of a circle with equation:
   x² + y² - 6x + 8y – 11 = 0 (3 mks)
3. If (M + n): (M – n) = 8: 3. Find the ratio M: n. (3 mks)
4. Find the values of x that satisfies the equation
   Log(x + 5) = log 4 – log (x + 2) (3 mks)
5. The co-ordinates of the points A, B and C are (0,-4), (2, -1) and (8, 8) respectively. Use vector method to show that the points are collinear. (3 mks).
6. W varies directly as the cube of x and inversely as y. Find W in terms of x and y given that W = 80 when x = 2 and y = 5. (3 mks)
7. Without using mathematical tables, simplify in the form a√b (3 mks)
        2       -     2     
      3-√7       3+ √7
8. Expand ( 2 + x)⁵ in ascending powers of x up to the term in x³. Hence approximate the value of (2.03)⁵ to four significant figures. (3 mks)
9. A clothes dealer sold 3 skirts and 2 trousers for sh. 840. He also sold 4 shirts and 5 trousers for Ksh. 1680. Form a matrix to represent the above information ; hence find the cost of 1 shirt and 1 trouser. (3 mks)
10. Mumbua bought two grades of rice, grade A and grade B. She bought grade A at Sh. 42 per kg and grade B at Sh. 21 per kg. If she sold the mixture of the two grades at Sh. 39 per kg making a profit of 30%, at what ratio should she mix the two grades? (3 Marks)
11. In a transformation, an object with an area of 5 cm2 is mapped onto an image whose area is 30cm². Given that the matrix of the transformation find the value of x.(3 mks)
    
12. The first term of an arithmetic sequence is -7 and the common difference is 3.
    1. List the first six terms of the sequence; (1 mk)
    2. Determine the sum of the first 50 terms of the sequence. (2 mks)
13. Pipe A can fill an empty water tank in 3 hours while pipe B can fill the same tank in 5 hours. When the tank it can be emptied by pipe C in 15 hours. Pipe A and B are opened at the same time when the tank is empty. If one hour later pipe C is also opened. Find the total time taken to fill the tank. (4 mks).
14. Make t the subject of the formula (3 Marks)
          r       =    P  
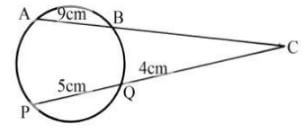
    √P² - t²         t
15. The figure below shows a circle centre O. AB and PQ are chords intersecting externally at a point C. AB = 9cm, PQ= 5cm and QC = 4cm. Find the length of BC. (3mks)
    
16. Using table of reciprocals of numbers, find the value of x if (3 Marks)
    x    =    1     +      3    
             25.36      1.302

SECTION II (50mks)
Answer only five questions in this section in the spaces provided.

17. OAB is a triangle in which OA = a and OB = b. M is a point on OA such that OM: MA = 2: 3 and N is another point on AB such that AN: NB = 1: 2. Lines ON and MB intercept at X.
    
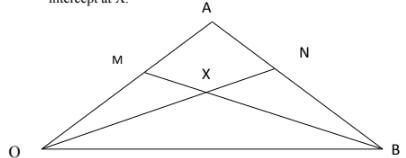
    1. Express the following vectors in terms of b  and  a .
       1. AB (1 mk)
       2. ON (2 mks)
       3. BM (1 mk)
    2. If OX = kON and BX = hBM express OX in two different ways. Hence or otherwise find the values of h and k. (5 mks)
    3. Determine the ratio OX: XN. (1 mk)
18.        
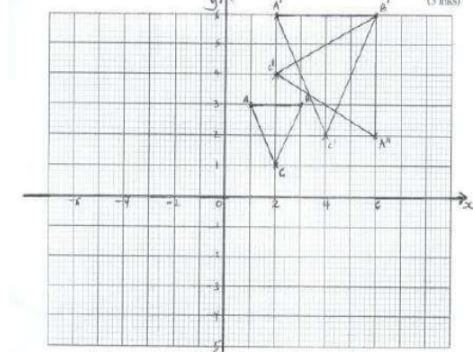
    1. Draw the graph of y = x3 + 2x2 − 5x − 8 for values of x in the range −4 ≤ x ≤ 3
       

       X	-4	-3	-2	-1	0	1	2	3
       X3	-64							27
       2X2
       -5x
       -8
       y	-20

       (5 mks)
    2. By drawing suitable straight line on the same axis, solve the equations.
       1. x³ + 2x² − 5x − 8 = 0 (1 mk)
       2. x³ + 2x² − 5x − 7 = 0 (2 mks)
       3. 3 + 3x − 2x² − x3 = 0 (2 mks)
19. A transformation represents by the matrix 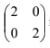 maps A(1, 3), B(3, 3) and C(2, 1) onto A¹B¹ and C¹ respectively.
    1. On the grid provided, draw the triangle ABC and its image A1B1C1on the same axes. (3 mks)
    2. Hence or otherwise determine the area of the triangle A¹B¹C¹(2 mks)
    3. Another transformation represented by the matrix 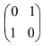maps A¹B¹C¹ onto A¹¹B¹¹C¹¹.Plot triangle A¹¹B¹¹C¹¹ on the same axes. (2 mks)
    4. Describe the transformation represented by the matrix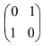(1 mk)
    5. Determine the matrix of the single transformation which maps A¹¹B¹¹C¹¹ onto ABC. (2 mks)
20. An examination involves a written and a practical test. The probability that a candidate passes the written test is ⁶/₁₁. If a candidate passes a written test then the probability of passing the practical test is ³/₅ , other wise it would be ²/₇.
    1. Illustrate this information on a tree diagram (2 mks)
    2. Determine the probability that a candidate
       1. Passes both tests ( 2 mks)
       2. Passes the written test only (2 mks)
       3. passes the practical test only (2 mks)
       4. Fails all test (2 mks)
21. Three partners Mutua, Muthoka and Mwikali contributed Sh. 600,000, Sh. 400,000 and Sh. 800,000 respectively to start a business of a matatu plying Mbumbuni – Machakos route. The matatu carries 14 passengers with each paying Sh. 250. The matatu makes two round trips each day and ever full. Each day Sh. 6000 is used to cover running costs and wages.
    1. Calculate their net profit per day. (2 mks)
    2. The matatu works for 25 days per month and is serviced every month at a cost of KSh.10, 000. Calculate their monthly profit in June. (1 mk)
    3. The three partners agreed to share 40% of the profit equally and 60% to be shared in the ratio of their contribution. Calculate Muthoka’s share in the month of July (4 mks)
    4. The matatu developed mechanical problems and they decided to sell it through an agent who charged a commission of 5% on selling price. Each partner received Ksh. 475,000 from the agent after he had taken his commission. Determine the price at which the agent sold the matatu. ( 3 mks)
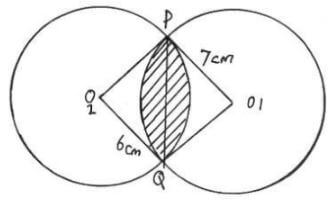
22. Two circles with centres O1 and O2, have radii 7cm and 6cm respectively. The two circles intersect at P and Q and the length of the common chord PQ is 10cm.
    
    Calculate the area of the shaded region in the above diagram to 4 significant figures. (10 mks)
23. The figure below is a right rectangular based pyramid VABCD where AB = 5cm, BC = 7cm,VC = 13cm and O is a point on the base of the pyramid vertically below V.
    
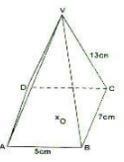
    Calculate
    1. AC (2 Marks)
    2. VO, the height of the pyramid. (2 Marks)
    3. the angle between the edge VB and the plane ABCD. (3 Marks)
    4. the angle between the planes VBC and ABCD. (3 Marks)
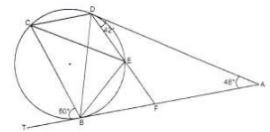
24. In the figure below, AT and AD are tangents to the circle at B and D respectively. DEF is a straight line, < CBT = 60º , < FAD = 48º and < ADF = 42º
    
    Calculate giving reasons, the value of:
    1. < DCE (2 marks)
    2. <BCE (2 marks)
    3. <DCB (2 marks)
    4. <DEC (2 marks)
    5. <BEF (2 marks)

MARKING SCHEME

1.    
   

   No	Log
   102.8043 Log 4.948 =0.6944 4.636 x 10-1	0.8043 +1.8416 0.6459 (3.6661)x1/2 4/2 + 1.666/2	0.6459 2.8331
   		1.8128

   10^0.8128 x 10¹ = 6.498x10¹ = 64.98
   
   
2. x²-6x+y²+8y=11
   x²-6x+(-3)²+y2+8y+(4)²=11+(-3)²+(4)²
   (x-3)²+(y-4)²=36
   (x-3)²+(y+4)²=62
   (3,-4)
   
   
3. ^m+n/_m-n = ⁸/₃
   3m+3n=8m-8n
   11n=5m
   ⁿ/_m = ⁵/₁₁
   m:n=11:5
   
   
4. Log(x-5)= Log4-Log(x+2)
   Log(x+5)=Log(⁴/_x+2)
   x+5=⁴/_x+2
   (x+5)(x+2)=4
   x2+2x+5x+10=4
   x2+7x+6=0
   x2+x+6x+6=0
   x(x+1)+6(x+1)=0
   (x+6)(x+1)=0
   x=-6 or x=-1    
   
   
5.   
   
6.     
   W=kx ²
          y
   80=k 2²
            5
   k=^80x5/₄=100
   w=100^x/_y
   
   
7.    2       -     2     
      3-√7       3+ √7
   = 2(3+ √7) -2(3- √7)
        (3-√7)(3+ √7)
   =(6+2√7) - (6+2√7)
       9 +3√7 -3√7 -7 
   = ^4√7/₂
   
   
8. Coeefficient→1,5,10,10
   (2+x)5 = 1(2⁵)(x)⁰ + 5(2⁴)(x)¹ + 10(2³)(x)² + 10(2²)(x)³
   =32+80x+80x²+40x³+...
   2+x=2.03
   x=2.03-2
   x=0.03
   (2.03)5=32+80(0.03)+80(0.03)²+40(0.03)³
   32+2.4+0.072+0.00108
   =34.47
   
   
9.  
   3x+27=840
   4x+5y=1680
   
10. 42x+21y =Sh.39 x¹⁰⁰/₁₃₀
       x+y
    42x+21y=30
       x+y
    42x+21y=30x-30y
    12x=9y
    ^x/_y=⁹/₁₂=³/₄
    x:y=3:4
    
    
11. Determinant= area side factor
    4x-(2(x-1))=³⁰/₅
    4x-2x+2=6
    2x=4 
    x=2
    
    
12.     
    1. nα= a+(n-1)d
       1st  a= -7
       2nd a+d =-4
       3rd a+2d=-1
       4th a+3d=2
       5th a+4d=5
       6th a+5d=8
       
       
    2.    
       Sn=ⁿ/₂[2a+(n-1)d]
       S50=⁵⁰/₂[2(-7)+(50-1)3]
       =25(-14+147)
       =25x133
       =3325  
13. Rate of work
    Pipe A=¹/₃ per hr
    Pipe B=¹/₅ per hr
    Pipe C=¹/₁₅ per hr
    Rate of work of A and B=¹/₃ + ¹/₅=⁸/₁₅ per hr
    Work done by and B in 1 hr
    ⁸/₅ x1= ⁸/₁₅
    1-⁸/₁₅=⁷/₁₅
    Raee of work of aall pipes= ¹/₃+¹/₈-¹/1₅=⁷/₁₅
    Time taken= ⁷/₁₅÷⁷/₁₅
    = 1 hr
    Total time taken = 1 + 1= 2hrs
    
    
14.        r       =    P  
    √P² - t²         t
    (      r       )²= (   P  )²
       √P² - t²            t  
           r²= p²
    p²-t²     t²
    r²t²=p²-p²t²
    r²t²+p²t²=p⁴
    t²(r²+p²)=p⁴
    t²=p⁴ 
    r²+p²
    t=     √p⁴
        r²+p²
    
    
15. AC.BC= PC.QC
    (9+x)x = 9x4
    x²+9x=36
    x²+9x-36=0
    x²+12x-3x-36=0
    x(x+12)-3(x+12)=0
    (x-3)(x+12)=0
    x-3=3, x=3
    or
    x+12=0, x=-12
    
    
16. ¹/_25.36 = ¹/_{2.536 x 10}
    0.3943 x 10^-1=0.03943
    ¹/₃₀₂ = 0.7680
    x=0.03943 + 3(0.7680)=2.343
    
    
17.     
    1.    
       1. AB=OB-OA
          =b-a
       2. ON=OA+AN
          =a+1/3(b-a)
          =a+1/3b-1/3a
          =2/3a+1/3b
       3. RM=OM-OB
          =2/5a-b
    2. OX=kON
       =k(2/3a + 1/3b)
       =(2/3ka + 1/3kb)........(i)
       OX=OB+BX
       =b+h(2/3a-b)
       =b+2/5ha-hb
       2/5ha+(1-h)b.........(ii)
       2/3ka+1/3kb=2/5ha+(1-h)b
       2/3k=2/5h
       10k=6h → 10k-6h=0 →5k-3h=0 ......(iii)
       1/3k=1-h
       k=3-3h → k+3h=3.......(iv)
       5k-3h=0
       k+3h=3
           6k=3
           k=¹/₂
    3. K=¹/₂
       OX=1/2ON
       OX:XN
       =1:1
18.    

    X	-4	-3	-2	-1	0	1	2	3
    X3	-64	-27	-8	-1	0	1	8	27
    2X2	32	18	8	2	0	2	8	18
    -5x	20	15	10	5	0	-5	-10	-15
    -8	-8	-8	-8	-8	-8	-8	-8	-8
    y	-20	-2	2	-2	-8	-10	-2	22

    
    
    1.  x=-2.8, x=-1.4, x=2.1
       
       
    2.  
       y=x³+2x²-5x=0
       0=x²+2x²-5x-7
       y=-1
       x=-2.9, x=-1.2 , x=2.05
       
       
    3. y=x³+2x²-5x-8
       0=x³-2x²+3x+3
       y= -2x-5
       x=-2.8, x=-0.9, x=1.4
       
       
19.     
    
    1.   
       
       
    2.       
       
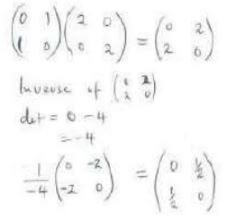
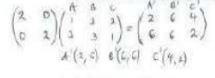
       Area of A¹B¹C^{1
       1}/₂ x 4 x 4
       8 sqr units
    3.     
       
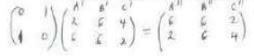
       A¹¹(6,2)
       B¹¹(6,6)
       C¹¹(2,4)
       
       
    4. Reflection is the mirror y=x     
20.        
    1.      
       
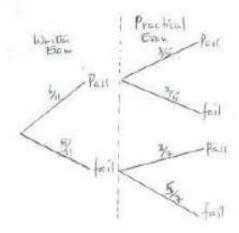
    2. Passes both tests
       ⁶/₁₁ x ³/₅ = ¹⁸/₅₅
    3. Passes written exam only
       ⁶/₁₁x²/₅
    4. Passess practice exam only
       ⁵/₁₁x²/₇=¹⁰/₇₇
    5. Fails all tests
       ⁵/₁₁x⁵/₇=²⁵/₇₇
21.         
    1. Total fare for 1 trip= 14x250=3500
       total amt for round trip=3500x4=14000
       Net profit =14,000 - 6,000=8,000
        
    2. Total amt for whole month   
       8000 x 25 =200,000
       Profit= 200,000-10,000=190,000
       
       
    3. Amt shared equally= ⁴⁰/₁₀₀ x 190,000
       Each got ⁷⁵⁰⁰⁰/₃ = 25,333
       Amt in ratio
       ⁶⁰/₁₀₀ x 190,000= 114000
       Ratio of contribution
       6:4:8
       matheka: ⁴/₁₈ x 114,000=25333
       Matheka's share= 25,333 + 25333= 50667
       
       
    4. Total amt received: 475,000 x 3= 1425,000
       
       
22.    
    1. Common line = 10cm
       half = 5cm
       Sin θ  = ⁵/₆
       θ= sin^-1(⁵/₆)
       = 56.49
       2θ=112.89
       Sin x = ⁵/₇
       x=sin^-1(⁵/₇)= 45.58
       2x=91.17
       
       Area of segment 1
       ^θ/₃₆₀πr² - ¹/₂r²Sinθ
       (^112.89/₃₆₀ x ²²/₇ x 6²)-(¹/₂ x 6² x Sin 112.89)
       35.48cm² - 16.58
       =18.9cm²
       
       Area of segment 2 = ^θ/₃₆₀πr²-1/2r²Sinx
       (^91.17/₃₆₀ x ²²/₇ x 7²)-(¹/₂x 7² x Sin 91.17)
       39.0-24.49cm²
       145.51cm²
       
       Area of shaded R= 18.9+14.51=33.41cm2
23.         
    1. AC=√52+72
    2. VO=√(132 - 4.3012)=12.27
    3. BD=AC=8.602
       BO=1/2 x 8.602=4.301 
       <VBO=θ
       Cos θ=4.301/13=0.3308
       θ=Cos-1(0.3308)=70.68
    4. VM=√(MO2 - VO2)=√(252 + 12.272)
       √(156.8029)=12.52
       <VMO=d
       Cos d=2.5/12.52=0.1997
24.        
    1. DCE=EDF(<s in alternate segement) =42º 
       BCE=BDF(<s in the same segment)
       ^180-48/₂= 24
       
       
    2. DCB = DBF (<s in alternate segment)
       DBF=^180-48/₂=66
       
       
    3. CED=CBD(<s in the same segment)
       CBD=180-(60+60)(<s on straigth line)
       CED=54
       
       
    4. BEF=BCD(ext angle=opp. interior angle)
       24+42=66