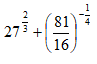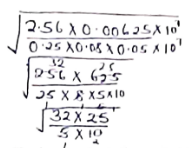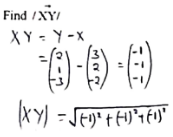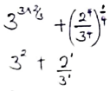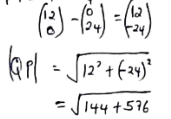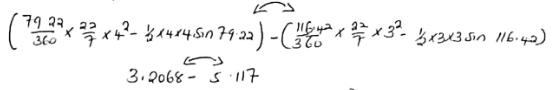Mathematics Paper 1 Questions and Answers - Form 4 Term 1 Opener Exams 2023

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Form 4 Term 1 Opener Exams 2023

Download PDF for future reference Get on Whatsapp for 50/-

INSTRUCTIONS

This paper consist of TWO sections: section I and Section II.
Answer ALL the questions in Section I and only five questions from section II.
Show all the steps in your calculations, giving your answers at each stage in the stage in the spaces below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.

SECTION I (50 Marks)
Answer all the questions in this section.

Without using mathematical tables or calculator, evaluate (3mks)
The length of a hollow cylindrical pipe is 6meters. Its external diameter is 11cm and has a thickness of 1cm. calculate the volume in cm³ of the material used to make the pipe. Take (π as 3.142) (3mks)
Simplify completely (3mks)
3y² − 1 − 2y + 1
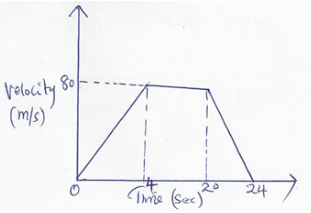
y² − 1 y + 1
The figure below is a velocity time graph for a car.
1. Find the total distance travelled by the car. (2 marks)
2. Calculate the deceleration of the car. (2 marks)
The exterior angle of a regular polygon is equal to one third of the interior angle. Calculate the number of sides of the polygon and give its name. (4mks)
Find the equation of the perpendicular bisector of line AB where A(3, 9) and B(7,5) giving your answer in the form ax + by + c = 0 (3 mks)
Given a: b = 6:7 and b: c = 14:17 find a: b: c. (2 mks)
Ruth is 12 years old. In three years’ time she will be ¹/₃ of his father’s present age. How old was her father 12 years ago. (3 mks)
The table below shows heights of 50 students
Height (cm) Frequency
140-144 3
145-149 15
150-154 x
155-159 11
160-164 2
1. State the medal class. (1mk)
2. Calculate the median. (3mks)
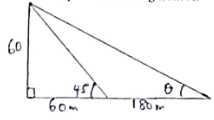
A man walks directly from point A towards the foot of a tall building 240m away. After covering 180m he observed that the angle of the top of the building is 45º. Calculate the angle of elevation of the top of the building from A. (3mks)
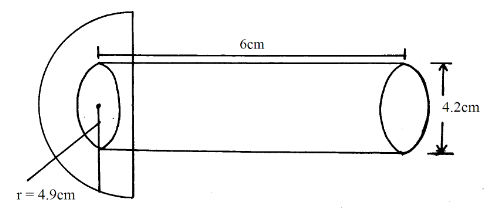
A plug is made up of hemispherical cup of radius 4.9cm and a cylinder of diameter 4.2cm and height 6cm as shown in the diagram alongside. Calculate the volume of the plug. (Take π as ²²/₇) (3mks)
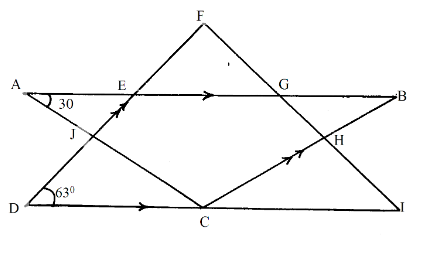
In the figure below AB is parallel to DI and FD is parallel to CB. Angle EAJ = 30º and angle EDC = 63º. Find angle ACB. (3mks)
→ →
The position vectors of point X and Y are x = 2i + j – 3k and = 3i + 2j – 2k, respectively.
→
Find /XY/ (3mks)
If takes 30 workers 6 days working 8 hours a day to harvest maize in a farm. How many days would 50 workers working 6 hours a day take to harvest the maize? (3mks)
Given that sin (x + 30) - Cos (3x) = 0 find the value of x without using tables or a calculator. (3mks)
Without using mathematical tables or calculation, evaluate: (3mks)

SECTION II 50 marks
Answer any 5 (five) questions in this section

In the year 2001 the price of a sofa set in a shop was Ksh. 12,000
1. Calculate the amount received from the sales of 240 sofa sets that year. (2mks)
2. In the year 2002 the price of each sofa set increased by 25% while the number of sofa sets sold decreased by 10%
  1. Calculate the percentage increase in the amount received from the sales. (3mks)
  2. If at the end of the year 2002, the price of each sofa set changed in the ratio 16:15. Calculate the price of each sofa set in the year 2003. (1mk)
3. The number of sofa sets sold in the year 2003 was P% less than the number sold in the year 2002. Calculate the value of P given that the amount received from sales in the year 2002 and 2003 were equal. (4mks)
A straight line passes through points (8, -2) and (4, -4)
1. Write its equation in the form ax + by + c = 0 where a, b and c are integers. (3 marks)
2. If the line in (a) above cuts the x axis at point P, determine the coordinates of P. (2 marks)
3. Another line which is perpendicular to the line in (a) above passes through point P and cuts the Y axis at the point Q. Determine the co-ordinates of point Q. (3 marks)
4. Find the length of QP. (2 marks)
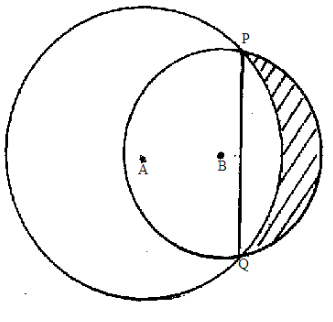
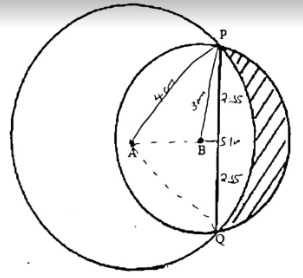
The figure below shows two intersecting circles with their centres A and B on one side of the chord PQ.

Given that the radius AP is 4cm, radius BP is 3cm and the chord PQ is 5.1cm. Line AB meets chord PQ at 90º.
1. Calculate the length of AB (3mks)
2. The area of the shaded region (7mks)

Complete the table below for the function y = x³ + 6x² + 8x (3mks)

x	−5	−4	−3	−2	−1	1
x³	−125	−64		−8	−1	1
6x²		96	54		6	6
8x	−40		−24	−16		8
y			3	0	−3	15

Draw the graph of the function y = x³ + 6x² + 8x for −5 ≤ x ≤ 1 use a scale of 2cm to represent 1 unit on the x-axis and 1cm to represent 2units on the y-axis. (3mks)
Use your graph to estimate the roots of the equations;
1. x³ + 6x² + 8x = 0 (1mk)
2. x³ + 5x² + 4x = −x² + 3x – 1 (3mks)

1. A triangle with vertices A(-4, 2), B(-6, 6) and C(-6,2) is enlarged by a scale factor -1 and centre (-2, 6) to produce triangle A’B’C’. Draw triangle ABC and its image on the grid provided. State the coordinates of A’B’C’ (3mks)
2. Triangle A’B’C’ in (a) above is reflected in line y = x to give triangle A”B”C” draw it on the same grid as in ‘a’ (3mks)
3. Triangle A”B”C” in ‘b’ above is mapped onto A”’B”’ and C”’ whose coordinates are A”’(0, -2), B”’(4, -4) and C”’(0, -4) by a rotation. Find the centre and angle of rotation (4mks)
A bus left Makindu at 11.45 a.m and traveled towards Mombasa at an average speed of 80km/h. A Nissan Matatu left Makindu at 1.15 p.m on the same day and traveled along the same road at an average speed of 120km/hr. The distance between Makindu and Mombasa is 400km.
1. Determine the time of the day the Nissan overtook the bus. (5 marks)
2. Both vehicles continue towards Mombasa at their original speeds. Find how long the Matatu had to wait at Mombasa before the bus arrived. (5 marks)
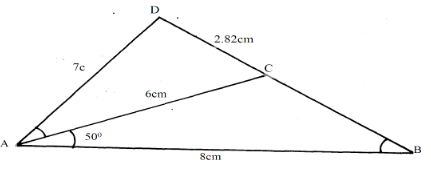
In the figure below (not drawn to scale) AB = 8cm, AC = 6cm, AD = 7cm, CD = 2.82cm and angle CAB = 50º.

Calculate to 2 decimal places;
1. The length BC (2mks)
2. The size of angle ABC (3mks)
3. The size of angle CAD (3mks)
4. The area of triangle ACD (2mks)
A particle moves a long straight line such that its displacement S meters from a given point is S = t³ – 6t² + 9t + 3 where t is the time in seconds. Find;
1. The displacement of the particle at t = 3
2. The velocity of the particle where t = 4.
3. The value of t when the particle is momentarily at rest.
4. The acceleration of the particle when t= 4.

MARKING SCHEME

SECTION I (50 Marks)
Answer all the questions in this section.

Without using mathematical tables or calculator, evaluate (3mks)

√³²/₂
= √16
= 4
The length of a hollow cylindrical pipe is 6meters. Its external diameter is 11cm and has a thickness of 1cm. calculate the volume in cm³ of the material used to make the pipe. Take (π as 3.142) (3mks)
3.142 × (5.5)² × 600 = 57027.3 cm³
3.142 × (4.5)² × 600 = 38175.3 cm³
57027.3 − 38175.3
= 18852
Simplify completely (3mks)
3y² − 1 − 2y + 1
y² − 1 y + 1
3y² − 1 −(2y+1)(y−1)
(y²+ 1)(y−1)
3y² − 1 − (2y² − y −1)
(y+ 1)(y−1)
3y² − 1 − (2y² + y +1)
(y+ 1)(y−1)
y² + y
(y+1)(y−1)
y(y+1)
(y+1)(y−1)
= y
y−1
The figure below is a velocity time graph for a car.
1. Find the total distance travelled by the car. (2 marks)
  A= distance = ½ (24 + 16)80
  = 1600m
2. Calculate the deceleration of the car. (2 marks)
  a = 0 − 80
  24 − 20
  ⁻⁸⁰/₄= −20
  deceleration = 20m/s²
The exterior angle of a regular polygon is equal to one third of the interior angle. Calculate the number of sides of the polygon and give its name. (4mks)
Let the interior angle be x
exterior angle = ¹/₃x
x + ¹/₃x = 180°
⁴/₃x = 180°
x = 135°
exterior = ¹/₃ × 135 = 45
n = 360 = 8 (Octagon)
45
Find the equation of the perpendicular bisector of line AB where A(3, 9) and B(7,5) giving your answer in the form ax + by + c = 0 (3 mks)
m₁ = 5 − 9 = −4 = −1
7 − 3 4
m₁×m₂ = −1
m₂ = ⁻¹/₋₁ = 1
midpoint = (3+7 , 9+5)
2 2
(5, 7)
y − 7 = 1
x − 5 1
y − 7 = x − 5
y = x + 2
x − y + 2 = 0
Given a: b = 6:7 and b: c = 14:17 find a: b: c. (2 mks)
a:b:c
6:7
14:17
84:98:119
Ruth is 12 years old. In three years’ time she will be ¹/₃ of his father’s present age. How old was her father 12 years ago. (3 mks)
Now I In 3 yrs time I 12 yrs ago
Ruth 12 15 0yrs
x x+3 x −12
3 × 15 = 1/3x × 3
x = 45
x − 12 = 45 − 12
= 33 yrs
The table below shows heights of 50 students
Height (cm) Frequency
140-144 3
145-149 15
150-154 x
155-159 11
160-164 2
1. State the medal class. (1mk)
  150 - 154
2. Calculate the median. (3mks)
  ½ × 50 = 25th position
  149.5 + (25 − 18)5
  19
  149.5 + 1.842
  = 151.342
A man walks directly from point A towards the foot of a tall building 240m away. After covering 180m he observed that the angle of the top of the building is 45º. Calculate the angle of elevation of the top of the building from A. (3mks)

tan 45 = h/60
h = 60m
tan θ = 60 = 0.25
240
θ = tan⁻¹0.25= 14.036°
A plug is made up of hemispherical cup of radius 4.9cm and a cylinder of diameter 4.2cm and height 6cm as shown in the diagram alongside. Calculate the volume of the plug. (Take π as ²²/₇) (3mks)

Vol of hemisphere = ²/₃ × ²²/₇ × 4.9³ = 246.50cm³
Vol. of cylinder = ²²/7 × 2.1² × 6 = 83.16
Total vol. = 246.50 + 83.16 = 329.66cm3
In the figure below AB is parallel to DI and FD is parallel to CB. Angle EAJ = 30º and angle EDC = 63º. Find angle ACB. (3mks)

∠ ACB = 87°
→ →
The position vectors of point X and Y are x = 2i + j – 3k and = 3i + 2j – 2k, respectively.
→
Find /XY/ (3mks)

= 1.7321 units
If takes 30 workers 6 days working 8 hours a day to harvest maize in a farm. How many days would 50 workers working 6 hours a day take to harvest the maize? (3mks)
W D H
30 6 8
50 x 6
X = 6 × ⁸/₆ × ³⁰/₅₀ = 4.8days
Given that sin (x + 30) - Cos (3x) = 0 find the value of x without using tables or a calculator. (3mks)
Sin(x+30) = Cos 3x
x + 30 + 3x = 90
4x = 60
x = 15°
Without using mathematical tables or calculation, evaluate: (3mks)

9 + ²/3 = 9²/₃

SECTION II 50 marks
Answer any 5 (five) questions in this section

In the year 2001 the price of a sofa set in a shop was Ksh. 12,000
1. Calculate the amount received from the sales of 240 sofa sets that year. (2mks)
  12000 × 240
  = Sh. 2,880,00
2. In the year 2002 the price of each sofa set increased by 25% while the number of sofa sets sold decreased by 10%
  1. Calculate the percentage increase in the amount received from the sales. (3mks)
    Sofa sets = 0.9 × 240 = 216
    Price per set = 1.25 × 12000
    = Sh 15000
    15000 × 216
    = Sjhs 3,240,000
    3240000 − 2880000 = 360000
    360000 × 100% = 12.5% increase
    2880000
  2. If at the end of the year 2002, the price of each sofa set changed in the ratio 16:15. Calculate the price of each sofa set in the year 2003. (1mk)
    ¹⁶/₁₅ × 15000
    = 16000
    = Sh 16000
3. The number of sofa sets sold in the year 2003 was P% less than the number sold in the year 2002. Calculate the value of P given that the amount received from sales in the year 2002 and 2003 were equal. (4mks)
  3240000 = 202.5
  16000
  216 − 202.5
  = 13.5
  13.5 × 100%
  216
  = 6.25% decrease
A straight line passes through points (8, -2) and (4, -4)
1. Write its equation in the form ax + by + c = 0 where a, b and c are integers. (3 marks)
  gradient = −y−−2 = −2 = ½
  4 − 8 −4
  ½ = y −−4
  x − 4
  2y + 8 = x − 4
  x − 2y − 12 = 0
2. If the line in (a) above cuts the x axis at point P, determine the coordinates of P. (2 marks)
  ^x/₁₂ − ^2y/₁₂ = ¹²/₁₂
  ^x/₁₂ + ^y/₋₆ = 1
  P(12,0)
3. Another line which is perpendicular to the line in (a) above passes through point P and cuts the Y axis at the point Q. Determine the co-ordinates of point Q. (3 marks)
  ^2y/₂ =^x/₂− ¹²/₂
  y = ½x − 6
  m₁ = ½
  m₂ = ⁻¹/_½ = − 2
  ⁻²/₁ = y − 0
  x − 12
  y = −2x + 24
  ^2x/₂₄ + ^y/₂₄ = ²⁴/₂₄
  ^x/₁₂ + ^y/₂₄ = 1
  Q(0,24)
4. Find the length of QP. (2 marks)
  QP = P − Q
  
  = √720
  = 26.83 units
The figure below shows two intersecting circles with their centres A and B on one side of the chord PQ.

Given that the radius AP is 4cm, radius BP is 3cm and the chord PQ is 5.1cm. Line AB meets chord PQ at 90º.
1. Calculate the length of AB (3mks)
  √(3² − 2.55²) = 1.5803cm
  √(4² − 2.55²) = 3.0818cm
  AB = 3.0818 − 1.5803
  = 1.5015cm
2. The area of the shaded region (7mks)
  ^θ/₃₆₀ πr² − ½ ab sin θ
  Sin θ = 2.55 Sin θ = 2.55
  4 3
  θ = 39.61 × 2 θ = 58.21 × 2
  = 79.22° =116.42°
  
  5.117 − 3.2068 = 1.910cm²

Complete the table below for the function y = x³ + 6x² + 8x (3mks)

x	−5	−4	−3	−2	−1	1
x³	−125	−64	−27	−8	−1	1
6x²	150	96	54	24	6	6
8x	−40	−32	−24	−16	−8	8
y	−15	0	3	0	−3	15

Draw the graph of the function y = x³ + 6x² + 8x for −5 ≤ x ≤ 1 use a scale of 2cm to represent 1 unit on the x-axis and 1cm to represent 2units on the y-axis. (3mks)
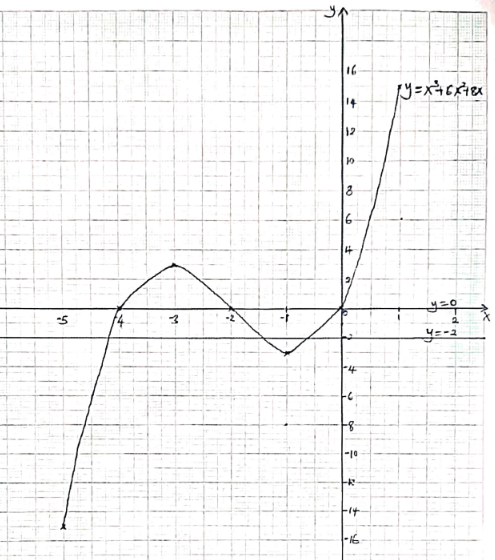
Use your graph to estimate the roots of the equations;
1. x³ + 6x² + 8x = 0 (1mk)
  y = 0
  x = −4 or −2 or 0
2. x³ + 5x² + 4x = −x² + 3x – 1 (3mks)
  x³ + 6x² + 8x = −2
  y = x³ + 6x² + 8x
  −2 = x³ + 6x + 8x
  y + 2 = 0
  y = −2
  x = −4.2 or x = −1.4 or x = −0.6

1. A triangle with vertices A(-4, 2), B(-6, 6) and C(-6,2) is enlarged by a scale factor -1 and centre (-2, 6) to produce triangle A’B’C’. Draw triangle ABC and its image on the grid provided. State the coordinates of A’B’C’ (3mks)
  
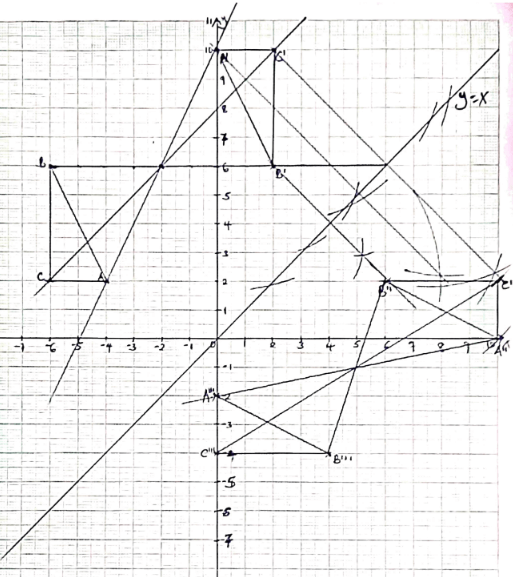
  A'(0.10) B'(6,2) C'(2,10)
2. Triangle A’B’C’ in (a) above is reflected in line y = x to give triangle A”B”C” draw it on the same grid as in ‘a’ (3mks)
  A"(10.0) B"(6,2) C"(10,2)
3. Triangle A”B”C” in ‘b’ above is mapped onto A”’B”’ and C”’ whose coordinates are A”’(0, -2), B”’(4, -4) and C”’(0, -4) by a rotation. Find the centre and angle of rotation (4mks)
  Centre of rotation = (5, −1)
  Angle of rotation ±180°
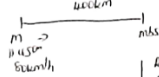
A bus left Makindu at 11.45 a.m and traveled towards Mombasa at an average speed of 80km/h. A Nissan Matatu left Makindu at 1.15 p.m on the same day and traveled along the same road at an average speed of 120km/hr. The distance between Makindu and Mombasa is 400km.
1. Determine the time of the day the Nissan overtook the bus. (5 marks)
  
  Mat
  1.15pm
  120km/h
  13.45
  −11.45
  1.30
  D = S × T
  = 80 × ³/₂
  = 120km
  R.D = 120km
  R.S = 120 − 80 = 40km/h
  R.T = ¹²⁰/₄₀ = 3hrs
  1.15
  3.00
  4.15p.m
2. Both vehicles continue towards Mombasa at their original speeds. Find how long the Matatu had to wait at Mombasa before the bus arrived. (5 marks)
  Tmat = ⁴⁰⁰/₁₂₀ = 3hrs 12min
  Arrival time mat = 1.15
  3.20
  4.35pm
  Tbus = ⁴⁰⁰/₈₀ = 5 hrs
  Arrival time bus = 11.45
  5.00
  1645hrs
  16.45
  −16.35
  10mins
  The matatu waited for 10minutes
In the figure below (not drawn to scale) AB = 8cm, AC = 6cm, AD = 7cm, CD = 2.82cm and angle CAB = 50º.

Calculate to 2 decimal places;
1. The length BC (2mks)
  a² = b² + c² − abc cos A
  a² = 6² + 8² − 2 × 6 × 8 cos 50
  a² = 38.29
  a = 6.185
  BC = 6.19cm
2. The size of angle ABC (3mks)
  b = a
  sin B Sin A
  6 = 6.19
  sin B Sin 50
  sin B = 6 sin 50
  6.19
  ∠ ABC = 47.95°
3. The size of angle CAD (3mks)
  a = b
  sin A Sin B
  9.01 = 7
  sin A Sin 47.95
  Sin A = 9.0 sin 47.95
  7
  ∠A = 72.878
  ∠LAD = 72.90 − 50
  = 22.90°
4. The area of triangle ACD (2mks)
  ½ab sin θ
  ½ × 6 × 7 sin 22.90
  = 8.17cm²
A particle moves a long straight line such that its displacement S meters from a given point is S = t³ – 6t² + 9t + 3 where t is the time in seconds. Find;
1. The displacement of the particle at t= 3
  S = t³ – 6t² + 9t + 3
  = 3³ − 6(3)² + 9(3) + 3 = 27 - 54 + 27 + 3 = 2 meters.
2. The velocity of the particle where t = 4.
  ^dS/_dt = 3t² − 12t + 9.
  3(4)² − 12(4) + 9 = 48 - 48 + 9 = 9 m/s.
3. The value of t when the particle is momentarily at rest.
  dS/dt = 0
  t: 3t² - 12t + 9 = 0.
  (3t - 9)(t - 1) = 0
  t = 3 and t = 1.
  t = 1 second
4. The acceleration of the particle when t= 4.
  ^d²S/_dt² = 6t − 12.
  t= 4 is 6(4) − 12 = 12 m/s².