Physics Questions and Answers - Form 4 Mid Term 1 Exams 2023

INSTRUCTIONS TO STUDENTS

Answer all then question in the spaces provided after each questions.
You must show all your calculations /works giving correct SI units.
Keep your work as clean as possible.

Describe an experiment which you can perform to determine the volume of a stone using the following apparatus, measuring cylinder, water, string and stone. (3mks)
A cube having each edge 20mm is moulded into a sphere. Calculate the radius of the sphere in metres (3mks)
1. You are given three bars; one 15 magnetised with opposite poles at its ends. Another is magnetized with consequent poles. The third is not magnetized. Describe an experiment which you would perform to identify each. (3 mks)
2. Explain the term particles and the kinetic theory
  1. The observation that if a perfume is sprayed at one and of a room, it can be detected by the sense of smell throughout the room. ( 1mk
  2. The process of diffusion is speed up by high temperatures (1mk)
An object is placed 10cm in front of a plane mirror. When the object is moved 4cm towards the mirror, calculate the distance between the object and the image (4mks)
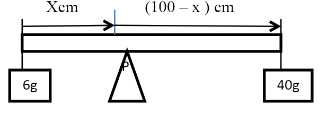
A metre rule of negligible weight has 40g and 60g masses suspended at ends of the ruler. What position must the ruler be supported so that it balances horizontally (4mks)
An object dropped from a height h, attains a velocity of 6m/s, just before hitting the ground. Find the height, h and (ii) the time taken to reach the ground. Take g=10m/s² (6mks)
State the two laws of refraction of light and energy. (2mks)
The velocity of light in water is 2.2×10⁸ m/s. Calculate the:-
1. Refractive index of light passing from water to diamond (3mks)
2. Also determine /calculate the angle of refraction in the diamond given that the angle of incidence is 40° in water (3mks)
1. Name 3 factors which affect the internal resistance to the flow of an electric current in a system (3mks)
2. State three methods used to measure the resistance of an unknown resistor (3mks)
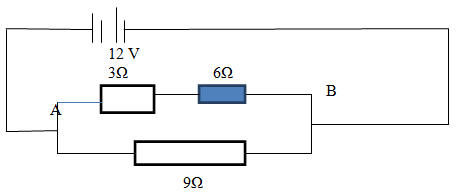
In the circuit below, determine
1. Total resistance between A and B (3mks)
2. Total effective resistance in the circuit (2mks)
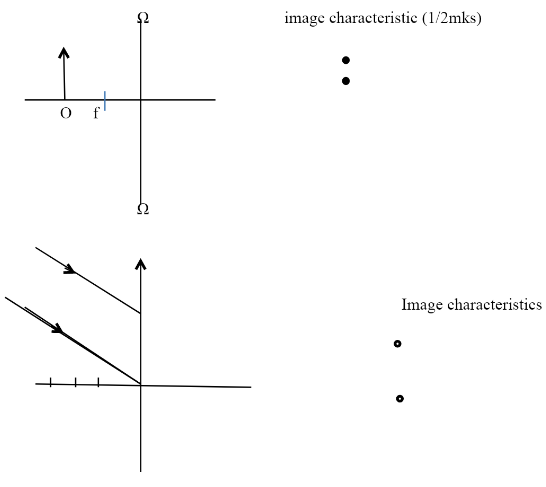
Define the following terms in relation to convex and diverging lens
1. Principal axis. (1mk)
2. The centre of curvature. (1mk)
3. Principal focus (1mk)
Sketch the following diagrams and state 2 characteristics of the image formed. (2mks)
1. arrange the following waves in order of increasing frequency. Visible light, Infra-red radiation, X-ray, U.V. radiation, Radio waves, and gamma rays. (1mk)
2. Calculate the wavelength of ultra violet light of frequency 7.5 x 10 Hz. (3mks)
1. State Archimedes principle. (1mk)
2. A solid object has a volume of 50cm³ and density of 0.8g/cm³. Calculate the weight of the water displaced when it is floating freely.
  (take g=10Nkg^-1) (3mks)
1. State four applications of uniform circular motion (2mks)
2. A rotating object moves at a rate of 90 rev/min.
  1. Calculate its angular velocity (2mks)
  2. Also determine its periodic time. (2mks)
1. State the following laws of electromagnetic induction. (1mk)
  1. Faraday’s law
  2. Lenz’s law (1mk)
2. Calculate the number of turns on the primary coil of a transformer which will enable a 40V appliance to be used with a 240a.c. mains power if there are 1000 turns on the secondary. (3mks)
State three reasons why transmission of electric power from the generating station, at high voltage is not transmitted by cables over buildings. (3mks)
A convex lens of local length 12cm forms an image on the screen which is 20cm away from the lens. Find the position of the object. (3mks)

MARKING SCHEME

Describe an experiment which you can perform to determine the volume of a stone using the following apparatus, measuring cylinder, water, string and stone. (3mks)
- Fill the measuring cylinder partially with water (Note the volume V1cm of the water)
- Tie the stone with the string and lower it gently in the cylinder until fully submerged.
  (Note the new volume of the water V₂cm
- The volume of the stone Vcm is calculated from
  Vcm + (V₂ – V₁)cm³
A cube having each edge 20mm is moulded into a sphere. Calculate the radius of the sphere in metres (3mks)
Vol. of the cube = (20x20x20) mm³ = 8000mm³
Vol. of asphere= ⁴/₃πr³ = vol of a cube
= ⁴/₃πr³ = 800mm³= 3 √8000 x 3mm³
4π
= 12.41mm or 0.01241M
1. You are given three bars; one 15 magnetised with opposite poles at its ends. Another is magnetized with consequent poles. The third is not magnetized. Describe an experiment which you would perform to identify each. (3 mks)
  - Suspend all the three bars and let them settle. The one that settles in N-S direction is magnetized with opposite poles at the ends.
  - Use the magnet above to test the other two bars.
  - The one that repels or attracts same end of the magnet is magnetized bar with consequent poles.
  - The one that does not repel same ends of magnet is not magnetized.
2. Explain the term particles and the kinetic theory
  1. The observation that if a perfume is sprayed at one and of a room, it can be detected by the sense of smell throughout the room. ( 1mk
    - Matter is made of particles that diffuse into the air
  2. The process of diffusion is speed up by high temperatures (1mk)
    - the particles gain more energy which in turn causes particles to move faster thus increasing the rate of diffusion
An object is placed 10cm in front of a plane mirror. When the object is moved 4cm towards the mirror, calculate the distance between the object and the image (4mks)
Distance between the object and the mirror’s
U=(10 - 4)cm=6cm which is
=image distance (v) = 6cm
Distance between object and image
=(6+6)cm= 12
Distance = 12cm
A metre rule of negligible weight has 40g and 60g masses suspended at ends of the ruler. What position must the ruler be supported so that it balances horizontally (4mks)

Sum of d moment= sum of A/c/moments
40(100-x) = X x 60
4000 – 40x = X x 60(60x)
X= 4000 = 40cm
100
Pivot is 40cm from 60g mass or the rule should be supported at 60cm from 40g mass
An object dropped from a height h, attains a velocity of 6m/s, just before hitting the ground. Find the height, h and (ii) the time taken to reach the ground. Take g=10m/s² (6mks)
Intial velocity, v = om/s, final vol = 6m/s
From v² = v2 + 2hg
62 = o² + 2 x 10xh
36 = 20h
H = (36)m = 1.8m
20
H = 1.8m
(ii) V = v + gt
6 = o + 10t
T= ⁶/₁₀ = 0.6
T = 0.6 seconds (deny of not units
State the two laws of refraction of light and energy. (2mks)
1. The incident ray, the refracted ray and the normal at the point of incidence, all lie in the same plane
2. The ratio of the sine of angle of incidence (i) to the sinc of the angle of refraction (r) is a constant for a given pair of media
3. Nb deny mark if ^{sin i}/_{sin r} = constant
The velocity of light in water is 2.2×10⁸ m/s. Calculate the:-
1. Refractive index of light passing from water to diamond (3mks)
  Wnd = vol of light in water
  Vol of light in diamond
  = 2.2 x 108ms (water) ie
  Vol of light diamond
  = 2.2 x 10⁸ = 1.774
  1.24 x 10⁸The refractive index of M2(diamond = 1.774 (no units)
2. Also determine /calculate the angle of refraction in the diamond given that the angle of incidence is 400 in water (3mks)
  wnd = sin 40° =1.774
  sin r
  sin r = sin 40°
  1.774
  R=sin^-I (sin 40°)
  (1.774)
  = 21.24°
1. Name 3 factors which affect the internal resistance to the flow of an electric current in a system (3mks)
  - Temperature
  - Length of the conductor
  - Thickness/cross sectional area of conductor
2. State three methods used to measure the resistance of an unknown resistor (3mks)
  - The wheatstone bridge method
  - The metre bridge method
  - Voltmeter- Ammeter method
In the circuit below, determine
1. Total resistance between A and B (3mks)
  for resistance in series, total resistance
  Re = R1 + R2
  = (3 + 6)Ω
  = 9Ω
2. Total effective resistance in the circuit (4mks)
  r in parallel resistors is resistance due to parallel resistors (ie one 9Ωand total resistance across AB)
  1 = 1 + 1
  R_t R_e R₃
  = 1 + 1
  9 9
  ²/₉
  R_t = (⁹/₂) 9Ω = 4.5Ω
Define the following terms in relation to convex and diverging lens
1. Principal axis. (1mk)
  - It is the line joining the two centres of curvature and is not deviated
2. The centre of curvature. (1mk)
  - Is the centre of a sphere of which the lens surface is part.
3. Principal focus (1mk)
  - It is the point on the p.a to which rays parallel and close to the axis convergea refraction (convex) or appear to come from after refraction / diverging lens)
Sketch the following diagrams and state 2 characteristics of the image formed. (2mks)
1. arrange the following waves in order of increasing frequency. Visible light, Infra-red radiation, X-ray, U.V. radiation, Radio waves, and gamma rays. (1mk)
  - Radio waves, infra-red radiation, visible light, U-violet radiation, x-rays gamma rays (1mk)
2. Calculate the wavelength of ultra violet light of frequency 7.5 x 10 Hz. (3mks)
  Soln
  X = v/_f (but V= C= 3 x 10⁸m/s
  = 30x10
  7.5 x 10
  4.0x10^-7M Answer
1. State Archimedes principle. (1mk)
  - When a body is fully or partially immersed in a fluid, it experiences an up thrust which is equal to the weight of the fluid displaced by it.
2. A solid object has a volume of 50cm³ and density of 0.8g/cm³. Calculate the weight of the water displaced when it is floating freely. (take g=10Nkg^-1) (3mks)
  Solution
  Mass of object= Density x volume
  = (0.8 x 50)g = 40g
  Wgh of the object= (40/100x 10)= 0.4N
  By law of floation
  Wght of liquid displaced= wgh of floating body
  = 0.4N°
1. State four applications of uniform circular motion (2mks)
  - moon’s orbing round a planet ½mk
  - A vehicle rounding abend ½mk
  - Banking of roads ½mk
  - Centrifuge ½mk
2. A rotating object moves at a rate of 90 rev/min.
  1. Calculate its angular velocity (2mks)
    w. = o = 90x 2π
    t 60
    = 3π rads^-1
    =9.42 rads
  2. Also determine its periodic time. (2mks)
    T= 2π = (2π)
    W 3π
    8 s=0.675
1. State the following laws of electromagnetic induction. (1mk)
  1. Faraday’s law
    - The mg+d of the induced emf is directly proportional to the rate of which the conductor cuts the mgtic field lines
  2. Lenz’s law (1mk)
    - The direction of the induced current is such as to oppose the change causing it
2. Calculate the number of turns on the primary coil of a transformer which will enable a 40V appliance to be used with a 240a.c. mains power if there are 1000 turns on the secondary. (3mks)
  Solution
  Vs = 40V, Ns=1000 turns
  Vp = 240V Np= ?Vs = Ns
  Vp Np
  Np= 1000 x ²⁴⁰/₄₀= 6000 turns
  Therefore 6000 turns of p. coil are required
State three reasons why transmission of electric power from the generating station, at high voltage is not transmitted by cables over buildings. (3mks)
- High risk of electrical shock
- Undesirable effects of strong electric field
- Risk of five when cables interact for any reason.
A convex lens of local length 12cm forms an image on the screen which is 20cm away from the lens. Find the position of the object. (3mks)
Use ¹/_v + ¹/_u = ¹/_f, f = +12cm, v = +20cm
U = ?
¹/_u = ¹/_f – ¹/_v
¹/₁₂ − ¹/₂ = 5-3
60
²/₆₀ − ¹/₃₀
U = 30cm in front of lens