Mathematics Paper 1 Questions and Answers - Form 4 End Term 1 Exams 2023

1. Without using mathematical tables or calculators evaluate. (3mks) 
   450 × √0.36
     81^¾ ÷ 27^²/₃
2. A line passing through points P (4, a) and Q (3, 2) is perpendicular to the line 3y + x + 3 = 0. Find the value of a and write down equation of line PQ. (4 marks)
3. Simplify; (3 marks)
      8 − 12x   −  4x − 7
   6x² −7x+2     3 − 6x
4. A positive two digit number is such that the product of the digits is 24. When the digits are reversed, the number formed is greater than original number by 18. Find the number. (3 marks)
5. During a certain period the exchange rates at a Pesa point were;
             Buying shs      Selling shs
   Riyal    19.68                 19.78
   A tourist arrived with 5480 Riyal which he changed to Kshs. He spend ²/₃ of the total in visiting various sites. As he was leaving he changed all he had to Riyal. How much did he leave with?      Answer to 1 d.p. (3 marks)
6. From a viewing tower 30metres above the ground, the angle of depression of an object on the ground is 30° and the angle of elevation of an aircraft vertically above the object is 42°.Calculate the height of the aircraft above the ground. (3mks)
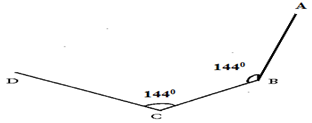
7. The figure below shows part of a regular polygon not drawn to scale.
           
   1. Determine the number of sides of the polygon. (2mks)
   2. Calculate the sum of interior angles of the polygon. (1mk)
8. Given that  a =   and b = .Find the percentage error in evaluating ^b/_a given that the values of a and b used are a = 0.45 and b = 1.5.Give answer correct to 2dp      (3mks)
9. The heights of two similar pails are 12cm and 8cm.The larger pail can hold 2 litres.What is the capacity of the smaller paid? (3mks)
10. If x = ²/₃ is a root of 6x² + kx – 2 = 0, find the value of k and the other root. (4 marks)
11. Tap A takes 4 minutes to fill a tank and tap B takes 6 minutes to empty the tank. If the tank has a capacity of 3000 litres find the volume of the tank after 2 minutes when both taps are open.   (3 marks)
12. Jim is 12 years old. In three years time he will be ¹/₃ of his father’s present age. How old was his father 12 years ago. (2 marks)
13. Solve the following inequality and show your solution on a number line.              (3 marks)
    4x – 3 ≤ ½ (x + 8) < x + 5
14. The midpoint of a vector PQ whose P (1, −4) and Q (x, y) is (−2, 5).
    1. Find the values of x and y. (2 marks)
    2. Calculate the length of PQ to 4 s.f (2 marks)
15. Using tables evaluate. (3marks)
       1      + ∛0.787+ (0.934)³ 
    34.52
16. Determine the equation of the normal to the curve y = 3x² – 4x + 1 at the point (2, 5).   (3marks)

SECTION B:ATTEMPT ANY FIVE QUESTIONS 

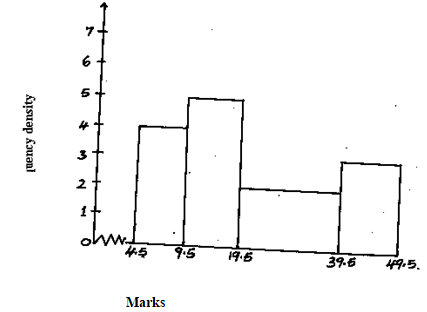
17. The diagram below shows a histogram representing the marks obtained in a certain test
           
    1. Prepare a frequency distribution table of the data (3mks)
    2. From above , estimate:-
       1. the mean mark (4mks)
       2. State the modal class (1mk)
       3. the median mark (2mks)
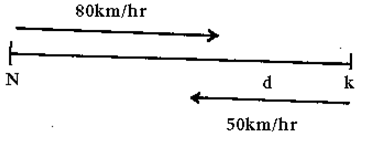
18. A bus travels from Nairobi to Kakamega and back.The average speed from Nairobi to Kakamega is 80km/h while that from Kakamega to Nairobi is 50km/h. It takes the bus three more hours to travel from Kakamega to Nairobi.
    1. Determine the distance between the two towns. (4mks)
    2. At 50km/h the fuel consumption is 0.35litres per km and at 80km/h the consumption is 0.3litres per kilometer. Find
       1. the total fuel consumption for the round trip (3mks)
       2. the average fuel consumption per hour for the round trip. (3mks)
19. A particle P moves in a straight line such that t seconds after passing a fixed point Q. it’s velocity is given by the equation 2t2 -10t + 12 find:
    1. The values of t when p is instantaneously at rest. (2 marks)
    2. An expression for the distance moved by P after t seconds.        (2 marks)
    3. The total distance traveled by P in the first 3 seconds after passing point O. (3 marks)
    4. The maximum velocity attained by the body. (3 marks
20. Triangle ABC has co-ordinates A(2, 0) B (2, 2) and C(0, 2).
    Using the squared grid  determine;
    1. The co-ordinates of triangle A¹B¹C¹, the image of triangle ABC under reflection in line x = 0. (3 marks)
    2. The co-ordinates of triangle A¹¹B¹¹C¹¹ and D¹¹, the image of triangle ABC under rotation of 90° clockwise centre (0, 0). (3 marks)
    3. The co-ordinates of triangle A¹¹¹B¹¹¹C¹¹¹, the image of triangle ABC under enlargement centre (0, 0) scale factor −1. (2 marks)
    4. The single transformation which maps triangle A¹¹¹B¹¹¹C¹¹¹ to triangle A¹B¹C¹. (2 marks)
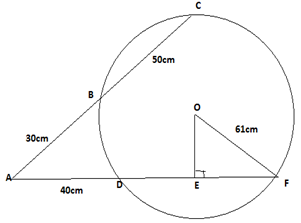
21. In the figure below OF is the radius of the circle centre O chords EDC and CB are extend to meet at A and OE is perpendicular to DF at E. OF = 61cm, AB= 30cm, BC = 50cm, AD= 40cm.
             
    1. Calculate the length of
       1. DF      ( 2marks)
       2. OE      (2marks)
    2. Calculate correct to 1dp
       1. Size of angle EOF ( 2marks)
       2. The length of the major arc DF ( 3marks)
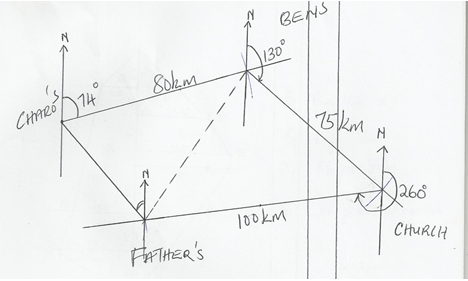
22. Every Sunday, Chalo drives a distance of 80km on a bearing of 074° to pick up his brother Ben to go to church. The church is 75km from Ben’s house on a bearing of S50°E. After church they drive a distance of 100km on a bearing of 260° to check on their father before Chalo drives to Ben’s home to drop him off then proceeds to his house.
    1. Using a scale of 1cm represent 10km show the relative positions of these places  (4 marks)
    2. Use your diagram to determine 
       1. The true bearing of Charo’s
       2. The compass of bearing of the father’s home from Ben’s home (1 marks)
       3. The shortest distance between Ben’s home and father’s home. (2 marks)
       4. The total distance Charo travels’ every Sunday. (2 marks)
23.  
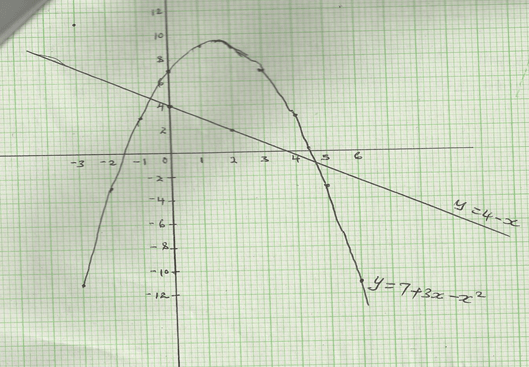
    1. Given that y = 7 + 3x – x², complete the table below          2mks
       

       x	–3	–2	–1	0	1	2	3	4	5	6
       y	–11			7						–11

    2. On the grid provided and using a suitable scale draw the graph of y = 7 + 3x – x². (3 marks)
    3. Use your graph to solve:
       1. X² – 3x – 7 = 0 1mk
       2. x² – 4x – 3 = 0   (3 marks)
    4. Determine the coordinates of the turning point of the curve. (2 marks)
24. The income tax rates in a certain year are as shown below.
    

    Income (k₤ – p.a)	Rate (Ksh. per ₤)
    1           – 4200	2
    4201     – 8000	3
    8001    – 12600	5
    12601  – 16800	6
    16801 and above	7

    Omar pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of KSh.10800 and is entitled to a personal relief of KSh. 1,100 per month. Determine:
    1. his gross tax per annum in Kshs (2 Marks)
    2. his taxable income in K₤ per annum (4marks)
    3. his basic salary in Ksh. per month  (2marks)
    4. his net income per month (2 marks)

MARKING SCHEME

1.	450 × √36/100   (34)¾ ÷ 27²/3   450 × 6/10     33 ÷ 32   45 × 6 = 45 × 6 = 90    33−2          3	M1  M1  A1
2.	3y = −x − 3   y = −x/3 − 1 GG2 = −1   G2 = 3 2 − a = 3 3 − 4 2 − a = − 3   a = 5 y − 5 = 3 x − 4 y − 5 = 3x − 12 y = 3x − 7	M1  B1  M1  M1
3.	−4(3x − 2)     −    4x − 7     (3x−2)(2x−1)      −3(2x−1)   −4     −    4x − 7     = 12 −  4x + 7  2x−1       −3(2x−1)       − 3(2x− 1)   =   19 −  4x        − 6x + 3	B1  B1  B1
4.	xy = 24 x = 24/y   ……………. i (10y + x) – (10x + y) = 18 9y – 9x = 18 y – x = 2 ………….ii substitute  y - 24/y  = 2 y2 – 2y – 24 = 0 y2 – 6y + 4y – 24 = 0 y(y – 6) + 4(y – 6) = 0 (y + 4) (y – 6) = 0 y – 6 = 0            x =  24/6   = 4 y = 6  ∴ The number is 46	M1  M1  A1
5.	1 Riyal buying = 19.68 shs   5480 = 107846.4  2/3 x 107846.4        = 71897.6 Remainder = 107846.4 – 71897.6                    = 35948.8 Selling 1 Riyal = 19.74 shs                ?       = 35948.8                        = 1817.4  Riyal	M1  M1  A1
6.	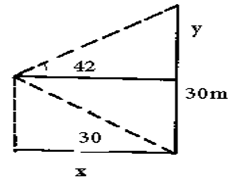x =   30      = 51.96       tan 30  y = 51.96 x tan42 = 46.79   = 79.79m	B1  M1  A1
7.	Exterior angle = 180 −  144 = 36 n = 360 = 10sides        36 Sum of interior angles = 180(n − 2)                                        =180(10 − 2)                                        =1440    Or 144*10=1440 B1	B1  A1  A1
8.	a=0.45      b=1.5 10a = 4.555  100a = 45.555 −10a = 4.555  90a = 41  a = 41/90 10b = 15.555 100b = 155.555 − 90b = − 140  b = 14/9 actual value of b/a = 14/9 × 90/4 = 140/41 value of b/a used 15/10 ÷ 15/100 = 10/3 error = 140/41 − 10/3 = 10/123 % error =  error  × 100 = 10/10                 actual  = 10/123 ÷ 140/41 × 100  = 2.381%	M1  A1
9.	L.S.F = 12:8 = 3:2 V.S.F = 27:8 iF 27 = 2litres      8  = ?  8/27 × 2 = 16/27 (16/27 × 1000)cm3  = 592.5926        = 0.59259	M1  M1  A1
10.	6x2 + kx – 2 = 0   x = 2/3 6(2/3)2  + k(2/3) − 2 = 0 8/3 + 2/3k = 2 2/3k = −2/3 K = -1 6x2 – x – 2 = 0 (2x + 1) (3x – 2) = 0 2x + 1 = 0    x = - ½	M1  A1  M1  A1
11.	Tap A in 1 minute ¼  Tap B in 1 minute 1/6 Retained ¼ − 1/6 = 1/12 In 2 min 1/12 x 2 = 1/6 Volume = 1/6 x 3000 = 500 litres	M1  M1  A1
12.	Present  3 yrs time   Jim  12   15 years   Father  15 × 3 = 45     Father 45 − 12 = 33 years	M1  A1
13.	4x – 3 < ½ ( x + 8) 4x – ½ x < 4 + 3      3 ½ x < 7            x  < 2 ½ x + 4 < x + 5          −1 < ½ x          −2 < x     −2 < x < 2          -2      -1       0       1       2	M1  M1  B1
14.	1 + X = −2       2 1 + x = − 4  x = − 5 −4+y = − 5     2 − 4 + y = − 10          y = − 6  Length PQ =                     = √(−6)2 + (−2)2                    = √40                     = 6.325 units	B1  B1  M1  A1
15.	1    + ³√0.787 + (0.934)3  34.52        1         + ∛(787/1000)  + (9.34/10)2 3.452 x 10 0.2901 x 0.1 + 9.233 x 0.1 + 814.8 x 0.001 0.02901 + 0.9233 + 0.8148 = 1.76711
16.	dy = 6x – 4  dx At x = 2, gradient of tangent  dy = 6(2) – 4      = 8 Gradient of normal = −1/8  Equation of normal is y – 5 = − 1/8                                    x – 2  8(y – 5) = −1(x – 2)  8y – 40 = − x + 2  8y         = − x + 42 x + 8y = 42 y= −1x + 21       8        4	B1  M1    A1
17.	Class  x     f   fx   c.f  5-9  7  20  140  20  10-19  14.5  50  725  70  20-39  29.5  40  780  110  40-49  44.5  30  1335  140      Σf = 140  Σfx = 2980     mean = Σfx = 2980               Σf      140          = 21.286 10 -19 median = 9.5 + 70 − 20 × 10                              30               = 9.5 + 10                = 19.5	B1   B1   B1   B1   B1   B1   B1   B1   B1
18.	t1 = d/s = d/80 the time diff = 3hrs  t2 = d/50     d/50 − d/80 = 3  = 80+ 50d = 3        400 = 30d = 1200        d = 40km   The fuel consumption at 50km/hr 1km → 0.35 at 80km/hr = 40 × 0.3 = 14litres   = 12litres Total fuel consumed = 14 + 12 = 26 t1 = 40/50 = 4/5 × 60 = 48                = 0.8hrs t2 = 40/80 = 0.5hrs Total timetaken = 0.8 + 0.5 = 1.3hrs Average fuel consumption = 26 = 20litres/hrs                                              1.3	A1  B1B1  A1  B1  B1  B1  B1
19.	V = 2t2 – 10t + 12 2t2 – 10t + 12 = 0  2        2      2 t2 – 5t + 6 = 0 t=3   or t = 2 ds = 2t2 – 10t + 12  dt S =∫ 2t3 −10t + 12 dt = 2/3t3 − 5t2 + 12t + c   2t3 −10t + 12 dt =  = 2/3t3 – st2 + 12t = 2/3(3)3 – 5(3)2  + 12(3)      18 – 45 + 36 = 9m At max velocity,a = dv/dt =0 a = dv/dt = 4t − 10 4t − 10 = 0 s = 2.5s v = 2 x 2.52 −10 x 2.5 + 12 = −0.5m/s	M1  A1  M1  A1  M1  M1  A1
20.		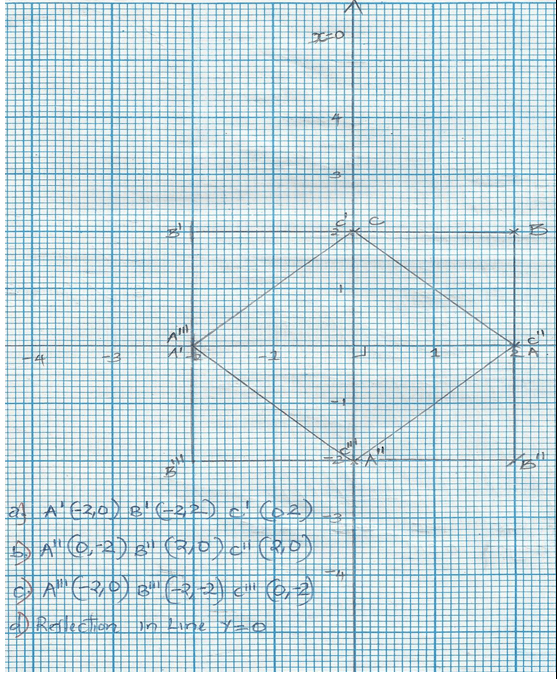S1 - Scale B1 - for ✓ΔABC drawn  B1 - for ✓co-ordinate of A¹B¹C¹ B1- for ✓centre used B1- for ΔA¹¹B¹¹C¹¹ drawn  B1 - for co-ordinate of A¹¹B¹¹C¹¹ B1 - for ✓Δ A¹¹¹B¹¹¹C¹¹¹ B1 - for ✓coordinate A¹¹¹B¹¹¹C¹¹¹ B2 - for ✓………allow B1 if not fully described
21.	AC x AB = AD x AF 80 x 30 = 40 x AF AF=60cm DF=60-40=20cm OE bisects DF EF = 10cm OE=√(612 − 102) = 60.17cm   Sin o = 10/61 = 0.1639 Angle O = 9.44 Angle DOF = 9.44 x 2 = 18.88 Reflex angle = 360 − 18.88 = 341.12 L= 341.12 x 2 x 22/7 x 61 = 363.32 cm         360
22.	True bearing of charo’s from father’s Compass bearing of fathers from Ben’s Distance  Ben’s and fathers 7.5 x 10 = 75km Distance (total)  by charo 2(100 + 75 + 80) = 510KM	M1 A1   M1 A1
23.	x  –3  –2  –1  0  1  2  3  4  5  6  y  –11  –3  3  7  9  9  7  3  –3  –11     X= −1.6,4.4 y = 7 + 3x – x2  0 = –3 – 4x + x2 y = 4 – x  x  0  2   y  4  2    x  1.5  y  9.2  Turning point (1.5, 9.2)
24.	(4000 x 12) +(1100 x 12)    = Sh. 61,200 1st slab 4200 x 8400 = 19800 2nd slab 3800 x 3 = 11400 3rd slab 4600 x 5 = 23000  42800 4th slab x 6 = (61,200 – 42800)    = K₤ 3066.70   = Taxable income  (12600 + 3066.70)    = K₤ 15666.7 (15666.7 x 20) − 10800          12 = KSh. 15,311.20 26111.20 – 4000 Sh. 22,311.20	A1 or 5100 x 2 M1   M1   M1     A1 M1 A2  M1 A1