Mathematics Paper 1 Questions with No Answers - Maseno Mock Exams 2020/2021

Kenya Certificate of Secondary Education 2020
121/2
MATHEMATICS -Paper 2
(ALT A)
2 ½ hours

Instructions to candidates

1. This paper consists of two sections: Section I and Section II.
2. Answer all the questions in Section I and only five questions from Section II.
3. Show all the steps in your calculations, giving your answers at each stage in the spaces provided below each question.
4. Marks may be given for correct working even if the answer is wrong.
5. Non – programmable silent electronic calculators and KNEC Mathematical Tables may be used, except where stated otherwise.

SECTION I: (50 Marks)

Answer all the questions in this section

1. Without using a calculator, find x if
   1 =     8 × −2 ÷ 4 +  3  
   x     −6  ÷ 2 × 5 − 3 + 4 (3 marks)
2. A fruit vendor bought 120 bananas at Sh. 6 each. He found that 3 bananas were bad. He sold some of the remaining bananas at Sh. 50 for every 6 and the rest at Sh. 20 for every 3 and realized a 25% profit. Find the number of bananas that he sold at Sh. 20 for every 3. (4 marks)
3. A rectangular room measuring 15.4 metres by 13.0 metres is covered by a number of whole square tiles with the largest possible dimensions. Calculate the least possible number of tiles required. (3 marks)
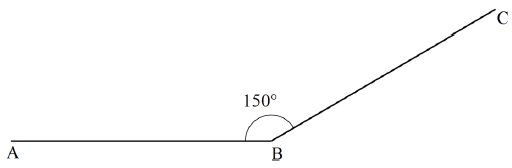
4. In the figure below, AB and BC are two sides of a regular polygon. ∠ABC = 150^o.
   
   Calculate the sum of the interior angles of the polygon. (3 marks)
5. Solve for x in the equation 4^(2x+0.5) − 16^(1+0.5x) = 8 − 4^x         (4 marks)
6.  An aircraft is vertically above a point P on a level ground. Munene observed the plane at the same time as Onyango, from the same ground, at an angle of elevation of 45^o and 30^o respectively. Given that Munene and Onyango are on the same side of P, and that Munene is 100 metres from P, calculate the distance between Munene and Onyango. (3 marks)
7. Use tables of logarithms to evaluate
   √(42.130.06588)
             3.5                                 (3 marks)
8. The following are the exchange rates that were used by a certain forex bureau in Kenya.
   

   Currency	Buying (Ksh)	Selling (Ksh)
   South African Rand	8.13	8.19
   Norwegian Krone	12.20	12.37

   A businessman from Norway converted 284,450 Norwegian Krone to Kenya shillings at the FOREX bureau.
   1. Find the amount of money that he received. (1 mark)
   2. The businessman spent Ksh. 2,355,000 while he was in Kenya. He then converted the balance to South African Rand. Calculate the amount of money, to the nearest Rand, that he received. (2 marks)
9. Five men working for 8 hours a day take 2 days to cultivate an acre of land. How many days would four men working 10 hours a day at double rate take to cultivate 3 acres of land? (3 marks)
10. Solve the inequality x − 3 ≤ 2(2 x + 1) < x + 12 giving your answer as a combined inequality hence illustrate the solution on a number line. (3 marks)
11. Given that and that the magnitude of AB is 13 units, find the possible values of x. (4 marks)
12. Using a ruler and a pair of compasses only, construct triangle PQR such that PQ = 7 cm, QR = 5 cm and angle PQ R = 105^o. Find the length of the perpendicular from R to PQ produced. (3 marks)
13. One – seventh of the money that was raised in a school harambee was used to renovate a staff house while two – thirds of the remainder was used for construction of a classroom. If Ksh. 630,000 remained still, calculate the much that was raised. (3 marks)
14. Given that  find B if AB⁻¹ = C (3 marks)
15. Simplify completely (3x + 2y)² − (3x  − 2y)². (2 marks)
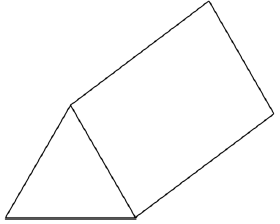
16. The figure below is a part of the sketch of a triangular prism 4 cm long. The cross section of the prism is an equilateral triangle of side 3 cm.
    
    
    1. Complete the sketch by drawing the hidden edges using broken lines. (1 mark)
    2. Hence draw the net of the prism. (2 marks)

SECTION II: (50 Marks)

Answer only five questions in this section

17. A straight line L₁ passes through the points P(5, −2)  and Q(−3, 4).
    1. Find the equation of L₁ in the form ax + by = c where a, b and c are integers. (3 marks)
    2. A line L₂ passes through a point R(0 , 3) and is perpendicular to L₁.
       1. Find the equation of L₂ in the form y = mx + c where m and c are constants. (2 marks)
       2. Determine the point of intersection between L₁ and L₂. (3 marks)
    3. Another line L₃ is parallel to L₁ and passes through R. Find the x – intercept of L₃. (2 marks)
18. Triangle ABC has vertices A (3, 2), B(6, 2) and C(5, 5) . The triangle A'B'C' is the image of triangle ABC after translation vector 
    1. On the grid below, draw the triangles ABC and A'B'C'. (2 marks)
       
    2. Triangle A"B"C" is the image of triangle A'B'C' after reflection in the line y = x + 1 . On the same axes, draw triangle A"B"C" and state its coordinates. (3 marks)
    3. Triangle A'''B'''C''' is the image of A"B"C" after a − 90^o turn about the origin (0,0). On the same axes, draw triangle A'''B'''C''' and state its coordinates. (3 marks)
    4. State the type of congruence between the triangles:
       1. ABC and A'B'C' . (1 mark)
       2. A'B'C' and A'''B'''C'''. (1 mark)
19. Two aeroplanes P and Q, leave an airport A for their respective destinations at the same time. P flies on a bearing of 240^o at an average speed of 800 km/h while Q flies due east at an average speed of 720 km/h.
    Calculate:
    1. The distance covered by P and Q after 45 minutes. (2 marks)
    2. The distance, to the nearest kilometre, between P and Q after 45 minutes. (3 marks)
    3. The bearing, to the nearest degree, of Q from P after 45 minutes. (3 marks)
    4. The shortest distance between the airport A and the direct path linking P and Q. (2 marks)
20. The table below shows the mass in kg of coffee delivered by farmers in a factory on a certain day.
    

    Mass(kg)	20-29	30-39	40-49	50-59	60-69	70-79
    No. of farmers	3	10	16	12	6	3

    1. State the class size of the distribution. (1 mark)
    2. Calculate, correct to 1 decimal place:
       1. The mean mass. (3 marks)
       2. The median mass. (3 marks)
    3. On the grid provided below, and on the same axes, draw a histogram and a frequency polygon to represent the information in the table. (3 marks)
       
21. A matatu left Nairobi at 7.00 a.m for Kisumu at an average speed of 75 km/hr. A car also left Nairobi 40 minutes later for Kisumu along the same route at an average speed of 105 km/hr.
    1. Determine:
       1. The time when the car caught up with the matatu. (4 marks)
       2. The distance from Nairobi when the car caught up with the matatu. (2 marks)
    2. A truck left Kisumu for Nairobi at 7.15 a.m at an average speed of 60 km/hr. If the truck met with the matatu at the same time as the car, find the time when the truck arrived in Nairobi. (4 marks)
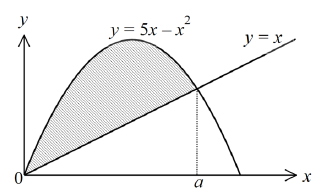
22. In the figure below, the shaded region is bounded by the curve y = 5 x − x² and the line y = x.
    
    
    1. Find a, the value of x at the point of intersection between the curve and the line. (1 mark)
    2. Estimate the area of the shaded region using:
       1. Trapezium rule with 4 strips. (3 marks)
       2. Mid – ordinate rule with 4 strips. (3 marks)
    3. Using integration, calculate the area of the shaded region (3 marks)
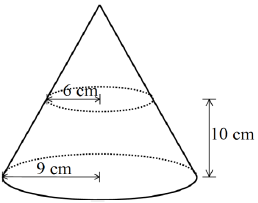
23. The figure below shows a closed conical vessel with water up to the height of 10 cm. The base radius of the container is 9 cm and the radius of the water surface is 6 cm.
    
    
    1. Giving your answer in terms of π , calculate the volume of water in the container. (4 marks)
    2. If the container is inverted vertically, find:
       1. An expression of the new height (h) in terms of the new radius (r) of water in the vessel. (2 marks)
       2. The value of r correct to 2 decimal places. (3 marks)
       3. The value of h correct to 2 decimal places. (1 mark)
24. The displacement s metres of a particle moving along a straight line after t seconds is given by:
    Calculate:
    1. The displacement of the particle by the time it comes to rest momentarily. (4 marks)
    2. The initial acceleration of the particle. (2 marks)
    3. The maximum velocity attained by the particle. (4 marks)