The figure below shows solid frustum of a pyramid with a square top of side 6cm and a square base of side 10cm. The slant edge of the frustum is 8cm.
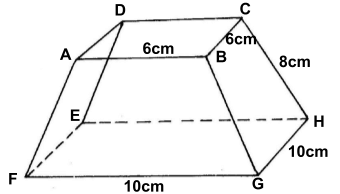
- Calculate the total surface area of the frustum
- Calculate the volume of the solid frustum.
- Calculate the angle between the planes BCHG and the base EFGH.