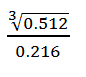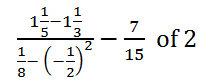SECTION I (50 MARKS)
Answer ALL the questions from this section.
- Find the reciprocals of 0.216 correct to 3 decimal places hence evaluate; (3 marks)
- Without using a calculator, evaluate; (4 marks)
- Three bells ring at intervals of 9 minutes, 15 minutes and 21 minutes. The bells will next ring together at 11.00pm. Find the time the bells had last rang together. (3 marks)
- Simplify the expression. (3 marks)
- Without using a calculator or mathematical tables, solve the equation. (4 marks)
2log10x−3log102+log1032=2
- A line L passes through point (3, 1) and is perpendicular to the line 2y = 4x + 5.
Determine the equation of line L. (3 marks)
- A forex bureau in Kenya buys and sells foreign currencies as shown below.
A businesswoman from China converted 195,250 Chinese Yuan into Kenya shillings.Buying Selling Currency Ksh Ksh Chinese Yuan 12.34 12.35 South African rand 11.28 11.37 - Calculate the amount of money in Kenya shillings that she received. (1 mark)
- While in Kenya, the businesswoman spent Ksh.1,258,000 and then converted the balance into South African Rand. Calculate the amount of money to the nearest Rand that she received. (3 marks)
- The seventh term of an A.P is 20 and the sum of the first 20 terms is 610. Find the first term and the common difference. (3 marks)
- The points P, Q and R lie on a straight line. The position vectors of P and R are 2i + 3j + 13k and 5i – 3j + 4k respectively. Q divides PR internally in the ratio 2 : 1. Find
- The position vector of Q. (2 marks)
- Distance of Q from the origin. (1 mark)
- In the figure below, <MNO = 54o, <PLM = 50o, PN = NM and PO is parallel to LM.
Find the value of <LPM.(3 marks)
- Two matrices A and B are such that
and
Given that the determinant of AB = 10, find the value of k. (3 marks)
- Two pipes A and B can fill an empty tank in 3 hours and 5 hours respectively. Pipe C can empty the full tank in 4 hours. If the three pipes A, B and C are opened at the same time, find how long they will take to fill the tank. (3 marks)
- Determine the equation of the normal to the curve y = x2 – 3x + 1 at a point (−2, 3) giving your answer in the form ax + by = c. (3 marks)
- The size of each interior angle of a regular polygon is five times the size of exterior angle.
Find the number of sides of the regular polygon. (3 marks) - Find the integral values of x which satisfy the inequalities.
x + 8>4x – 6≥3(4 – x) (2 marks) - John had two bags A and B containing sugar. If he removed 2kg from bag A and added to bag B, the mass of sugar in bag B would be four times the mass of sugar in bag A. If he added 10kg of sugar to the original amount of sugar in each bag, the mass of sugar in B would be twice the mass of the sugar in bag A.
Calculate the original mass of sugar in each bag. (3 marks)
SECTION II (50 MARKS)
Answer any FIVE questions from this section
- The table below shows the height measured to the nearest cm of 101 pawpaw trees.
Height in cm 20-24 25-29 30-34 35-39 40-44 45-49 50-54 55-59 Frequency 2 15 18 25 30 6 3 2 - State the modal class. (1 mark)
- Calculate to 2 decimal places.
- The mean height (4 marks)
- The difference between the mean height and the median height. (5 marks)
- Three pegs R, S and T are on the vertices of a triangular plan field. R is 300m from S on a bearing of 300o and T is 450m directly South of R.
- Using a scale of 1cm to represent 60m, draw a diagram to show the position of the pegs. (3 marks)

- Use the scale drawing to determine;
- The distance between T and S in metres. (2 marks)
- The bearing of T from S. (1 mark)
- Find the area of the field in hectares correct to one decimal place. (4 marks)
- Using a scale of 1cm to represent 60m, draw a diagram to show the position of the pegs. (3 marks)
- Mr. Mutuku owns a bicycle which he sometimes rides to go to work. Out of 21 working days in a month he only rides to work for 18 days. If he rides to work the probability that he is bitten by a rabid dog is 4/15 otherwise it is 1/13 only. When he is bitten by the dog, the probability that he will get treatment is 4/5 and if he does not get treatment the probability that he will get rabies is 5/7
- Draw a tree diagram to show the events. (3 marks)
- Using the tree diagram above determine the probability that
- Mutuku will not be bitten by a rabid dog. (2 marks)
- He will get rabies. (2 marks)
- He will not get rabies. (3 marks)
- The volume Vcm3 of a solid depends partly on r2 and partly on r3 where r is one of the dimensions of the solid. When r = 1, the volume is 54.6cm3 and when r = 2, the volume is 226.8cm3.
- Find the expression for V in terms of r. (5 marks)
- Calculate the volume of solid when r = 4. (3 marks)
- Find value of r for which the two parts of the volume are equal. (2 marks)
- The equation of a curve is given by y = 5x−x2
- Draw the curve of y = 5x−1/2x2 for 0≤x≤6 (3 marks)

- By integration find the area bounded by the curve, the line x = 6 and the x-axis. (3 marks)
-
- On the same graph in (a) draw the line y = 2x (1 mark)
- Determine the area bounded by the curve and the line y = 2x (3 marks)
- Draw the curve of y = 5x−1/2x2 for 0≤x≤6 (3 marks)
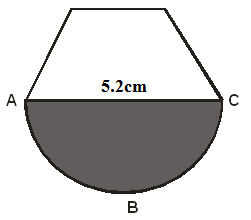
- The diagram below shows a cross section of a bottle. The lower part ABC is a hemisphere of radius 5.2cm and the upper part is a frustum of a cone. The top radius of the frustum is one third of the radius of the hemisphere. The hemisphere part is completely filled with water as shown in the diagram.
When the container is inverted, the water now completely fills on the frustum part.- Determine the height of the frustum part. (7 marks)
- Find the surface area of the frustum part of the bottle. (3 marks)
- A bus left Nairobi at 7.00a.m and travelled towards Eldoret at average speed of 80km/h. At 7.45am, a car left Eldoret towards Nairobi at an average speed of 120km/hr. The distance between Nairobi and Eldoret is 300km. Calculate
- The time the bus arrives at Eldoret. (2 marks)
- The time of the day the two vehicles met. (4 marks)
- The distance from Nairobi to where the two vehicles met. (2 marks)
- The distance of the bus from Eldoret when the car arrived at Nairobi. (2 marks)
-
- Complete the table below for the function y = 2x3 + 5x2 – x – 6. (3 marks)
x −4 −3 −2 −1 0 1 2 2x3 −128 −54 5x2 −x 4 3 −6 −6 −6 −6 −6 −6 −6 −6 y −50 −6 0 - Draw the graph of y = 2x3 + 5x2 – x – 6 for (3 marks)

- By drawing a suitable line, use the graph in (b) to solve the equations
- 2x3 + 5x2 + x – 4 = 0 (2 marks)
- 2x3 + 5x2 – x + 2 = 0 (2 marks)
- Complete the table below for the function y = 2x3 + 5x2 – x – 6. (3 marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download MATHEMATICS PAPER 1 - 2017 KITUI MOCK EXAMINATION.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students