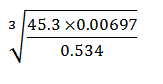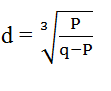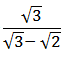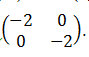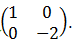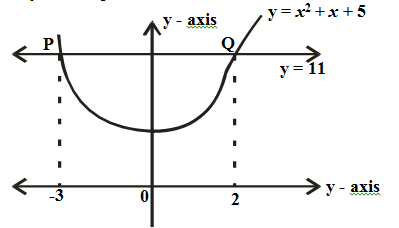SECTION I (50 MARKS)
Answer ALL the questions from this section.
- Use logarithms to evaluate, (4 marks)
- Make P the subject of the formula (3 marks)
- Find the circle centre and radius whose equation is
3x2 + 3y2 + 18x – 6y + 18 = 0 (3 marks)
- The volumes of two similar cylindrical containers are 27cm3 and 64cm3 Given that the height of the smaller container is 12cm, find the height of the larger container. (2 marks)
- 3cm3 of water is added to 2cm3 of a certain medicine which costs sh.12 per cm3. The chemist sells the diluted medicine at sh.6 per cm3. Calculate the percentage profit.
(3 marks) - Given that 4y = 3 sin 2/5 for 0 < θ< 360o. Determine
- The amplitude of the curve (1 mark)
- The period of the curve. (1 mark)
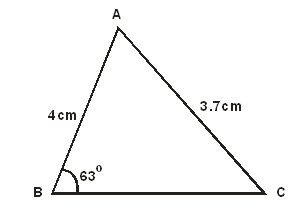
- Find the length BC of the following triangle if AC = 3.7cm, AB = 4cm and angle ABC = 63o. (3 marks)
- Solve for x in the equation
27x - 1 3x + 1 = 729 (3 marks)
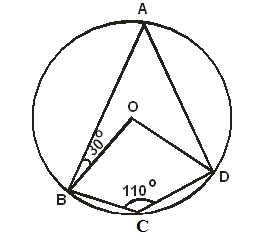
- In the figure below ABCD is a cyclic quadrilateral. Point O is the centre of the circle. <ABO = 30o and <BCD = 110o.
Calculate the size of angle ADB. (2 marks)
- Three people Mutua, Wanza and Kiilu contributed money to start a business. Mutua contributed a quarter of the money and Wanza two fifths of the reminder. Kiilu’s contribution was one and a half times that of Mutua. They borrowed the rest of the money from a bank which was sh.60,000 less than Kiilu’s contribution. Find the total amount required to start the business. (4 marks)
- Simplify (3 marks)
- Expand (2-1/4x)5 and use the first three terms to find the value of 1.9755 to four significant figures. (4 marks)
- The radius of a spherical ball is measured as 7cm correct to the nearest centimeter. Determine to 2 decimal places, the percentage error in calculating the surface area of the ball. (3 marks)
- Given that tan θ= 1/√5 where θ is an acute angle, find without using tables or calculator sin (90−θ) leaving your answer in the simplified surd form. (4 marks)
- Given that a = 1.2, b = 0.02 and c = 0.2, express ac b in the form where m and n are integers. (3 marks)
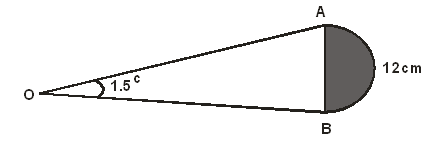
- The diagram below shows sector AOB of a circle centre O. <AOB = 1.5C and arc AB is of length 12cm.
- Determine the radius OA of the circle. (1 mark)
- Calculate the area of the shaded region. Give your answer correct to 3 s.f. (3 marks)
SECTION II (50 MARKS)
Answer any FIVE questions from this section
- The table below shows the taxation rates.
Mueni is housed by her employer but pays a nominal rent of sh.1200 per month. She is entitled to a personal relief of sh.950 per month. If her monthly P.A.Y.E is sh.7024,Income (£ per month) Rate (%) 0-382 10 383-754 15 755-1126 20 1127-1498 25 1499-1870 30 1871-2242 35 over 2242 40 - Calculate her gross income. (5 marks)
- In addition to the tax the following monthly deductions are also made
Sacco shares Ksh. 1200
Coop loan Ksh.1500
Union dues Ksh.300
Calculate- Her monthly salary. (3 marks)
- Net monthly salary (2 marks)
- Use a ruler and compasses only for all construction in this question.
- Construct a triangle ABC in which AB = 8cm, BC = 7.5cm and <ABC = 1121/20 . (3 marks)
- Measure the length of AC. (1 mark)
- By shading the unwanted region show the locus of P within the triangle ABC such that AP BP, AP > 3cm. Mark the required region as P. (3 marks)
- Construct a normal from C to meet AB produced at D. (1 mark)
- Locate the locus of R in the same diagram such that the arc of triangle ARB is the arc of the triangle ABC. (2 marks)
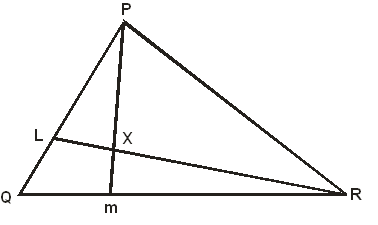
- In the triangle PQR below, L and M are points on PQ and QR respectively such that PL : LQ = 1 : 3 and Qm : mR = 1 : 2. Pm and RL intersect at X. Given that PQ = b and PR= c
- Express the following vectors in terms of b and c.
- QR (1 mark)
- Pm (1 mark)
- RL (1 mark)
- By taking PX = hPm and RX = kRL where h and k are constants. Find two expressions of PX in terms of h, k, b and c. Hence determine the values of the constants h and k. (6 marks)
- Determine the ratio LX : XR. (1 mark)
- Express the following vectors in terms of b and c.
- OABC is a parallelogram with vertices O(0, 0), A(2, 0), B(3, 2) and C(1, 2). OIAIBICI is the image of OABC under a transformation matrix.
-
- Find the coordinates of OIAIBICI (2 marks)
- On the graph provided, draw OABC and OIAIBICI (2 marks)
-
- Find OIIAIIBIICII, the image of OIAIBICI under the transformation matrix. (2 marks)
- On the same grid, draw OIIAIIBIICII. (1 mark)
- Find OIIAIIBIICII, the image of OIAIBICI under the transformation matrix. (2 marks)
- Find the single matrix that maps OIIAIIBIICII onto OABC. (3 marks)
-
- An aircraft leaves town P (30oS, 17oE) and moves directly towards Q (60oN, 17oE). It then moved at an average speed of 300 knots for 8 hours Westwards to town R. Determine
- The distance PQ in nautical miles. (2 marks)
- The position of town R. (4 marks)
- The local time at R if local time at Q is 3.12p.m (2 marks)
- The total distance moved from P to R in kilometers. (Take 1nm = 1.853km) (2 marks)
- The figure below is a sketch of a curve whose equation is y = x2 + x + 5. It cuts the line y = 11 at points P and Q.
- Find the area bounded by the curve y = x2 + x + 5 and the line y = 11 using the trapezium rule with 5 strips. (5 marks)
- Calculate the difference in the area if the mid-ordinate rule with 5 ordinates was used instead of the trapezium rule. (5 marks)
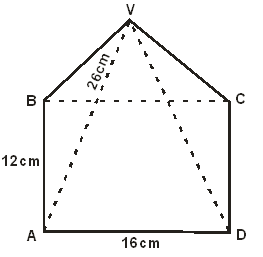
- The figure below represents a rectangular based pyramid VABCD. AB = 12cm and AD = 16cm. Point O is vertically below V and VA = 26cm.
Calculate:- The height, VO, of the pyramid. (4 marks)
- The angle between the edge VA and the plane ABCD. (3 marks)
- The angle between the planes VAB and ABCD. (3 marks)
- The distances S metres from a fixed point O, covered by a particle after t seconds is given by equation
S = t3 – 6t2 + 9t + 5- Calculate the gradient to the curve at t = 0.5 seconds. (3 marks)
- Determine the values of S at the maximum and minimum turning points of the curve. (4 marks)
- On the space provided, sketch the curve of S = t3 – 6t2 + 9t + 5. (3 marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download MATHEMATICS PAPER 2 - 2017 KITUI MOCK EXAMINATION.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students