General Geometric Shapes
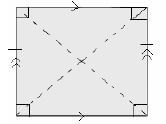
Square
- All sides are equal
- Opposite sides are parallel
- Each interior angle is a right angle (90º)
- The interior angles total up to 360º
- Diagonals bisect each other at right angles.
- Diagonals measure the same length and bisect interior angles.
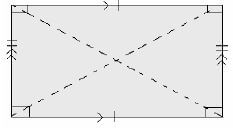
Rectangle
- Each interior angle is 90º and they all add up to 360º
- Diagonals are equal
- Diagonals bisect each other but NOT at right angles
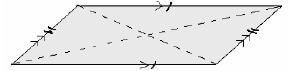
Parallelogram
- Opposite sides are equal and parallel
- Opposite angles are equal
- Diagonals bisect each other
- Diagonals are not equal
- Adjacent angles are supplementary (add up to 180º)
Rhombus
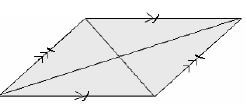
- All sides are equal
- Opposite sides are parallel
- Opposite angles are equal
- Diagonals bisect each other at 90º
- Diagonals bisect the interior angles
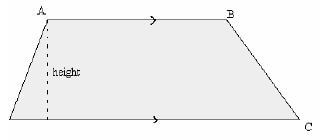
Trapezium
- The sum of the interior angles is 360º
- Has a pair of parallel lines which are not of the same length
- Has a perpendicular height joining the two parallel lines
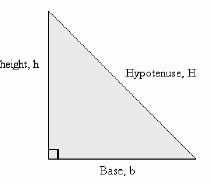
Right-angled Triangle (Pythagorean relationship)
- H2 = b2 + h2
- b2 = H2 – h2
- H2 = H2 - b2
Examples of relationships
Base Height Hypotenuse 3 4 5 6 8 10 5 12 13 7 24 25 8 15 17 9 40 41

Properties of Triangles and Parallel Lines
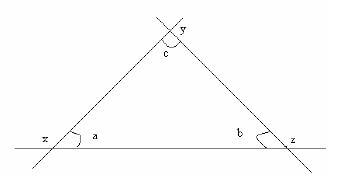
Triangle
Exterior angles & interior angles
- Angles x, y, and z are exterior angles while a, b, and c are interior angles.
- Exterior angles add up to 360º while interior angles add up to 180º.
- Angles x, a; b, z; and c, y; are adjacent to each other and they add up to 180º (supplementary angles)
Parallel Lines and Transversal
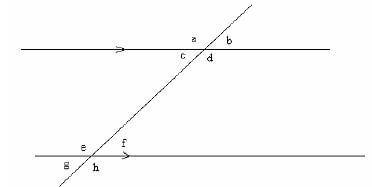
- Angles at a point e.g. a + b+ c + d = 360º
- Vertically opposite e.g. a/d, b/c, f/g, e/h. They are equal
- Corresponding angles e.g. b/f, a/e, c/g, d/h. They are equal
- Alternate angles e.g. c/f, d/e are always equal.
- Co-interior angles e.g. c/e, d/f, are always equal.
- Co-interior/allied angles e.g. c/e, d/f are formed by parallel lines. They are supplementary.

Speed, Distance and Time
The formulae related to speed, distance and time can be derived from the following triangle.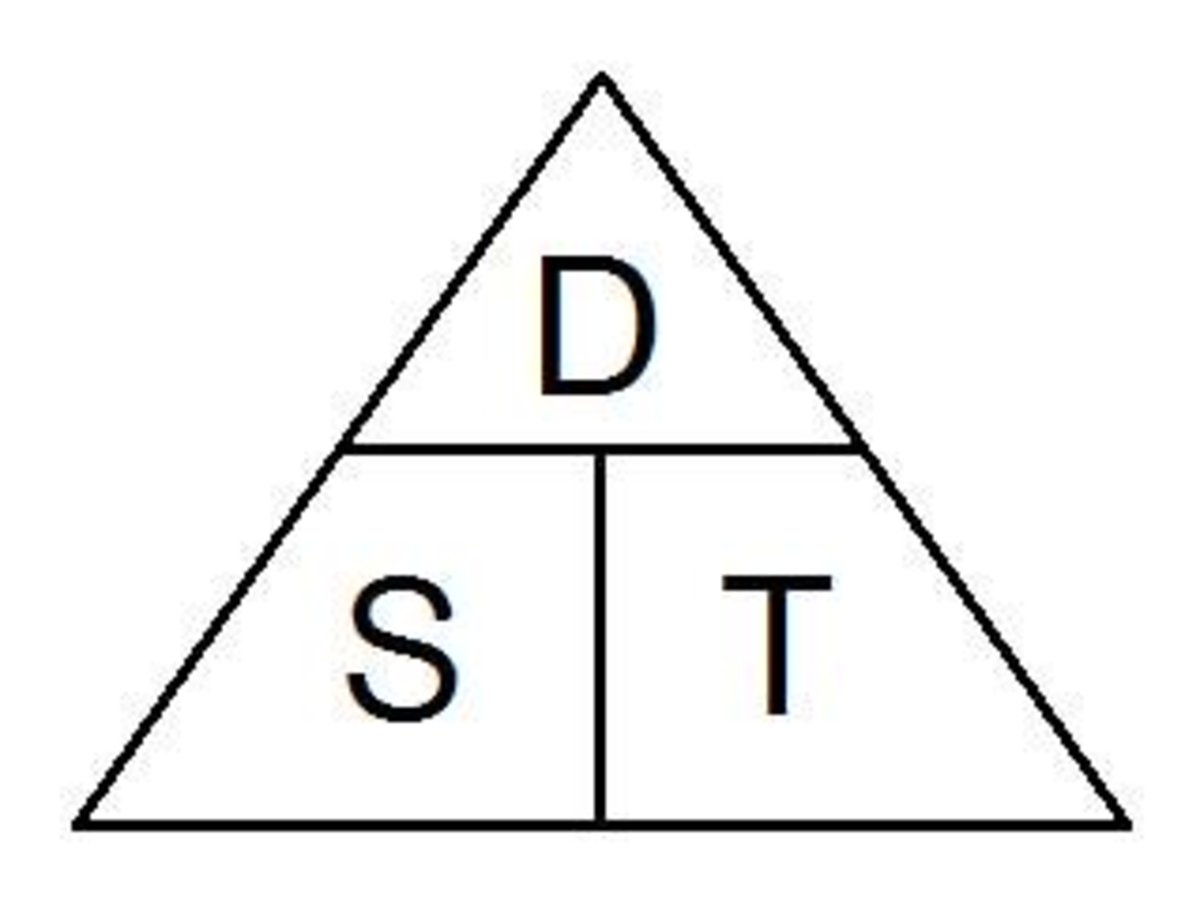
Join our whatsapp group for latest updates
Tap Here to Download for 30/-
Get on WhatsApp for 30/-
Download Properties of Geometric Shapes - Class 8 Mathematics Revision Notes.
Tap Here to Download for 30/-
Get on WhatsApp for 30/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students