Mathematics Paper 2 - Alliance High School Pre-Trial Examination 2018

Click the link below to download as a full set with all the subjects. (PDF)

https://downloads.easyelimu.com/details/35-Alliance_High_School_Pre_Trial_Examination

ALLIANCE HIGH SCHOOL
2018 PRE-TRIAL EXAM
MATHEMATICS
Paper 2
2¹/₂ hours

INSTRUCTIONS TO CANDIDATES

• The paper contains TWO sections: Section I and Section II
• Answer ALL the questions in section I and ONLY FIVE questions from section II.
• All answers and working must be written on the question paper in the spaces provided below each question.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I: ANSWER ALL QUESTIONS IN THIS SECTION (50 MARKS)

1. Use logarithm table to evaluate. (4 mks)
   
   
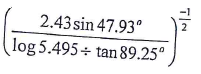
2. Gombe and Miheso working together can dig a piece of land in 4⁴/₅ days. Gombe working alone takes 4 days less than Miheso. How many days does Miheso take to dig the piece of land alone? (3 mks)
3. Given the co-ordinates of a point P is (-1,3,5) and Q is (2,-2,4) find:
   1. PG in terms of i,j,k (1 mk)
   2. The distance between P and Q (2 mks)
4. Without using a mathematical table or a calculator, evaluate leaving your answer in the form a + b√c
   
   
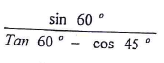
5. 1. Expand and simplify (x - y)⁵ (2 mks)
   2. Use the first four terms of the expansion to evaluate (-0.8)⁵ (2 mks)
6. A student expands (x - y)² as x² - y². If the student uses this expansion to evaluate (12-9)², find the percentage error in his calculation. (2 mks)
7. A sum of Ksh 10,000 is invested at 12% p.a compounded quarterly. After how many years will this sum amount to Ksh. 24,760? (3 mks)
8. 1. Using a ruler and a pair of compasses, construct triangle WXY such that WX = 6.4cm, XY = 6cm and <WXY = 60^o . (1 mk)
   2. Construct the locus of M such that <WMY + <WXY = 180^o (2 mks)
9. Find P^-1 if P = (²₃ ¹₂) hence use P^-1 to find the point of intersection of the lines 6x + 3y = 63 and 6x + 4y = 68 (3 mks)
   
10. A candidate in a certain school has 60% chance of passing an exam at the first attempt. Each time a candidate fails and repeats the exam; his chances of passing are increased by 15%. Calculate the probabilty that the candidate in the school passes an exam at the second or third attempt. (3 mks)
11. Determine the equation of the normal to the curve at x = 2 (3 mks)
    
    
    
    
    
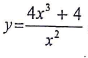
12. Make t the subject of the formula (3 mks)
    
    
    
    
    
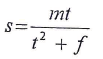
13. A value R is partly constant and partly varies as T. when T = 27, R =55 and when T = 57, R = 58. Find the relationship between R and T. (3 mks)
14. The points co-ordinates (6,1) and (-4,9) are the end points of a diameter of a circle centre A.
    1. Find the co-ordinates of A. (1 mk)
    2. Find the equation of the circle in the form x² + y² + ax + by + c = 0, where a, b and c are constants. (2 mks)
15. An industrialist has 450 liters of a chemical which is 70% pure. He mixes it with a chemical of the same type but 90% pure so as to obtain a mixture which is 75% pure. Find the amount of the 90% pure chemical used. (3 mks)
16. In the figure below, XY and YZ are chords of a circle centre O, XY = 5cm, YZ = 6cm and XZ = 9cm.
    
    
    
    
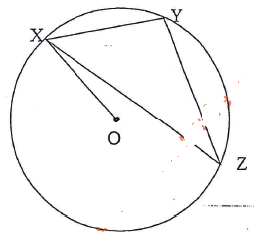
    1. Calculate <XYZ (2 mks)
    2. Calculate the length OX. (2 mks)

SECTION II: ANSWER ONLY FIVE QUESTIONS FROM THIS SECTION (50 MARKS)

17.  
    1. PQRS is a quadrilateral with vertices P(1,4) Q(2,1),R(2,3) and S(6,4). On the grid provided, draw the quadrilateral. (1 mark)
    2. Draw P'Q'R'S' the image of PQRS under a positive quarter turn about the origin and write down its coordinates. (3 marks)
    3. Draw P''Q''R''S'' the image of P'Q'R'S' under the transformation whose matrix is (¹_-2⁰₁) and write down its co-ordinates. (3 marks)
    4. Determine the matrix T of a single transformation that maps PQRS onto P''Q''R''S'' (3 mks)
18. The fourth, seventh, and sixteenth term of an arithmetic progression are in geometric progression. The sum of the first six terms of the arithmetic progression is 12.
    Determine the
    1. First term and the common difference of the arithmetic progression. (6 mks)
    2. Common ration of the geometric progression. (2 mks)
    3. Sum of the first six terms of the geometric progression. (2 mks)
19. On the same axes, draw the graph of y = 2 sin x and y = 3 sin (x + 30^o) for the domain 0^o ≤ x ≤ 360^o (5 mks)
    From your graph determine: 
    1. The period of each of the functions. (1 mk)
    2. The amplitude of each of the functions. (1 mk)
    3. The solution of 3 sin (x + 30^o) - 2 sin x = 0 (1 mk)
    4. The transformation that maps the graph of y = 2 sin x onto the graph of y = 3 sin (x + 30^o)  (2 mks)
20. A plane leaves P(75oN,30oE) and follows a longitude via the north pole flying at 300 knots to Q it takes 10hrs to reach point Q.
    1. Calculate
       1. The distance covered by the plane in nautical miles. (1 mk)
       2. The position of Q (4 mks)
    2. After spending 2 hours at Q, it then flies westwards to T which is 1360km west of Q, find:
       1. The longitude of T (using R = 6370km) to the nearest degree. (3 mks)
       2. The local time at T when the local time at Q is 5:30pm (2 mks)
21. Kipchumba makes two types of wedding cakes. Types A and B. Type A requires 200g of flour and 80g of cooking oil. Type B requires 400g of flour and 50g of cooking oil. On a particular day, they had 1600g of flour and 400g of cooking.
    1. If they make x cakes of type A and y cakes of type B, write down inequalities in x and y to represent the above conditions. (4 mks)
    2. Graph the inequalities in (a) above. (4 mks)
    3. The profit on type A cake is sh. 30 and the profit on type B cake is sh. 40. Determine the number of cakes of each type he should make to maximize profits. (2 mks)
22. The figure below represents a solid cuboid ABCDEFGH with a rectangular base. AC = 13 cm, BC = 5 cm and CH = 15cm. M is the midpoint of GH.
    
    
    
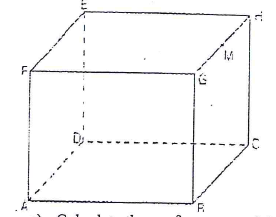
    1. Calculate the surface are of the cuboid. (3 mks)
    2. Calculate the angle between line AH and the base ABCD (2 mks)
    3. Calculate the angle between the base ABCD and the plane ADM. (2 mks)
    4. Calculate the angle betwen line AV and MF. (3 mks)
23. The table below shows the analysis of examiniation marks scored by 160 candidates.
    
    

    Marks %	1-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
    No. of candidates	2	6	15	22	36	34	20	15	6	4

    
    
    
    1. using an assumed mean of 45.5, calculate.
       1. The mean. (3 mks)
       2. The variance (2 mks)
       3. The standard deviation (2 mks)
    2. Calculate the semi interquartile range. (3 mks)
24.  
    1. Using the mid-ordinates rule, estimate the area under the curve y = 1/2 x 2 - 2, using six strips between x = 2 and x = 8 and x axis. (5 mks)
    2. 1. Use integration to determine the exact area under the curve. (3 mks)
       2. Find the percentage error in calculating the area using the mid-ordinate rules. (2 mks)