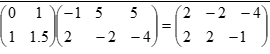Mathematics Paper 2 Questions and Answers - Cekana Mock Exams 2023

INSTRUCTION 

• The paper consists of two sections. Section I and Section II.
• Answer ALL the questions in Section I and any FIVE questions in Section II.
• Show all the steps in your calculations, giving your answer at each stage in the spaces provided
  below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silent electronic calculators and KNEC Mathematical tables may be used
  except where stated otherwise.
• Candidates should answer the questions in English.

QUESTIONS

SECTION A (50MARKS)
Answer All Questions in this section

1. The area of a rectangle is 48.4cm² and its length is 9.37cm. Calculate the percentage error in width (3marks)
2. The base of a triangle is (3x-2) cm. The height of the triangle is 5cm shorter than its base. Given that the area of the triangle is 25cm². Find length of the base. (4marks)
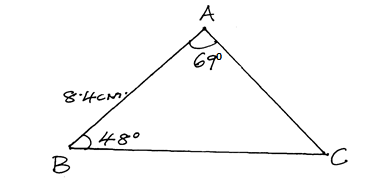
3. Find the area of the triangle shown below (3marks)
   
4. Express the following expression in surd form and simplify by rationalising the denominator (3marks)
   ²/ _1-tan30
5. Solve for x in the expression (log₂x)² + log₂x³=10 (3marks)
6. The table below is part of the tax for monthly income for the year 2007
   

   Monthly income (ksh)	Rate %
   Under ksh 10165	10
   From 10165 but under ksh19741	15
   From 19741 but under ksh29317	20

   
   In that year, John’s monthly gross tax was Ksh 2885. Calculate his monthly income (3marks)
7. A quantity E is partly constant and partly variaes as square root of F.
   1. Write down an equation connecting E and F where K and C are constants respectively.
   2. If F=25 where E=22 and F=49 when E=28. Find the value of K and C (3marks)
8.  
   1. Expand (1+ 1⁄2 x)⁷ in ascending power of x (1mark)
   2. Using the first four times of the expansion in (a) above estimate the value of (1 1⁄30)⁷ (2marks)
9. Find the number of terms of the series 5+8+11+14+17+……….. that will give a sum of 2183 (3marks)
10. Find the inverse of the matrix M= 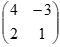 hence find the co-ordinates of the point at which
    line 4x-3y=4  and 2x+y=7 intersect (3marks)
11. A trader mixed grade I, II and III of coffee in the ratio 2:3:5 respectively. Grade I cost Sh650 per kg, grade II costs sh 500 per kg and grade III costs sh 420 per kg.
    1. Find the cost of one kg of the mixture (2marks)
    2. If the trader sold the mixture at a profit of 20% calculate the selling price of 3kg of the mixture (2marks)
12. Solve for the equation 4cos² x=5-4 sin x  for 0°≤ x ≤360 (3marks)
13. The figure below has a cross-section of the prism which is an isosceles triangle of side AE= 8cm, DE= 8cm and AD=6cm, where AB=20cm
    
    
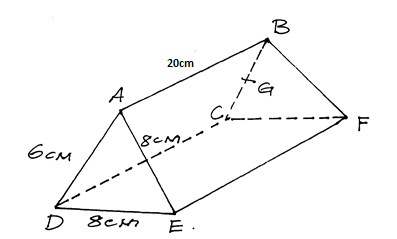
    1. If G is the mid- point of side BC find
       1. GF (1mark)
       2. AG (1mark)
    2. The angle between line DF and plane ABCD (2marks)
14.  
    1. Construct triangle PQR in which PQ=QR=5cm and angle PQR=90° (2marks)
    2. Draw the locus of S which moves in such a way that it is always on the same side of PR as Q and angle
       PSR =45°(1mark)
15. Determine the amplitude and period in the function y= 1⁄2 sin(3x-60) (2marks)
16. Two towns P and Q are located on the equator such that P is due east of Q. The distance between the two towns is 1920nm. If the latitude of p is 50°E. Determine the longitude of Q(3marks)

SECTION B (50 MARKS)
Answer any five questions from this section

17. The cost of Jane’s car at the beginning of year 2000 was sh 750,000. It depreciated in value by 7% per year for the first 3 years, by 8% for the next two years and 11% per year for the subsequent years.
    1. Find the value of the car at
       1. The start of the year 2003 (2marks)
       2. The end of year 2007 (3marks)
    2. At the beginning of 2008, Jane sold the car through Mary,s dealers at 22% more than its actual depreciated value to Lucy. Taking Mary’s sale price as the car’s value after depreciation. Find the average monthly rate of depreciation for the 8years. (5marks)
18. MNP is a triangle with vertices M,(2,2),N(2,-2) and P(-1,-4). Draw the triangle MNP. (1mark)
    1. If vertex N(2,-2) is mapped to N¹ (5,-2) by a shear with x-axis invariant, draw triangle M¹N¹P¹, the image of triangle MNP under the shear. (2marks)
       
    2. Find the matrix that represent the shear in (a) above (2marks)
    3. A transformation where matrix is T= (0  1) maps triangle M1N1P1 onto M¹¹N¹¹P¹¹. Draw the triangle M¹¹N¹¹P¹¹ (3marks)
                                                                  1  1.5
    4. Describe fully a single transformation that maps triangle M11N11P11 back onto triangle MNP and give its transformation matrix. (2marks)
19.  
    1. Complete the table below for the equation y=x³-3x²-5x+7  (2marks)
       
       

       x	-3	-2	-1	0	1	2	3	4	5
       y	-32		8	7	0		-8		32

    2. Draw the graph of  y=x³-3x²-5x+7(3marks)
       
    3. Use your graph to estimate the roots of the equation  x³-3x²-5x+7=0 (2marks)
    4. Use your graph to solve the equation  x³-3x²-10x+17=0 (3marks)
20. The table below shows marks scored by 40 students in a test
    

    Marks	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90
    frequency	1	5	8	12	7	4	2	1

    
    
    1. Calculate the upper quartile and lower quartile (4marks)
    2. If 30% of students failed the test, find the pass mark (3marks)
    3. The pass mark was set at 25 marks. How many students passed the test. (3marks)
21. The diagram below shows two intersecting circles with centres X and Y. HG is a tangent to the circle centre X at C. Angle GCE=70° and angle CEF=130°. Given that CB=5cm, BA=4cm, AE=12cm and radius DY=6cm.
    
    
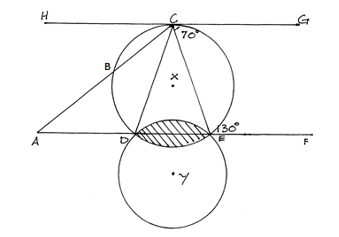
    1. Determine
       1. Angle DXE (2marks)
       2. Length DE (2marks)
       3. Angle DYE (2marks)
    2. Calculate the area of the shaded region (take π= 22⁄7) (4marks)
22.  
    1. Wekesa has two fair tetrahedral solids one red and other green. The faces of red solid are numbered 1to 4 while the faces of green solid are numbered 2,3,5 and 6. He tosses the two solids at the same time and recorded the number that is the bottom face of each solid. If k is the number that is at the bottom face of red solid while t is the number that is at the bottom face of green solid, find the probability that
       1. 2k+t=7 (1mark)
       2. (2k+t) is at most 9 (1mark)
       3. 2k≥t (2marks)
    2. In a group of 40 people, 10 are healthy and every person of the remaining 30 has either high blood pressure, a high level of cholesterol or both. Given that 15 have high blood pressure, 25 have high level of cholesterol and x have both. If a person is selected at random from this group. What is the probability that he/ she
       1. Has high pressure only (2marks)
       2. Has high level of cholesterol only (1mark)
       3. Hass high blood pressure and high level of cholesterol (1mark)
       4. Has either high blood pressure or high level of cholesterol (2marks)
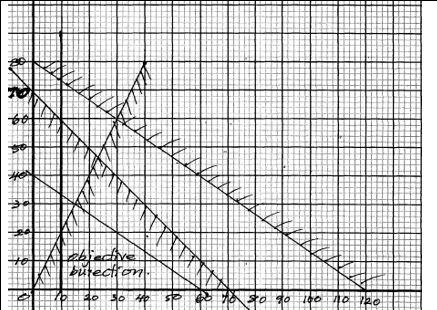
23. A company was contracted to transport 1200 tonnes of sand. The company used type A and type B trucks to do the job. Each type A truck carries 10 tonnes of sand per trip while B curries 15 tonnes per trip. The total number of trips must not be less than 70 and type B truck must make at least twice as many trips as type A truck while the later must make not less than 10trips. Taking x to represent the number of trips made by type A trucks and y to represent the number of trips made by type B trucks
    1. Write down all the inequalities representing the above information (4marks)
    2. Represent the inequality graphically (4marks)
    3. The company makes a profit of sh2000 per trip made by each type A truck and sh 3000 per trip made by each type B truck.
       1. Using a search line, determine the number of trips each type of truck must be made to maximise the profit (1mark)
       2. Hence calculate the maximum profit (1mark)
24.  
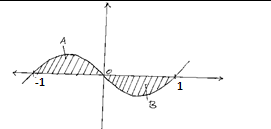
    1. Find the area of the region bounded by the cuver y=x³-x and the axes between the point x=-1 and x=1 (4 marks)
    2. At a certain instant a body is moving in a straight line at 20cm/s. Its acceleration during the first 5seconds of the subsequent motion is (30-6t) cm/s² where t is the time in seconds. After 5 seconds it travels with a constant speed. Find
       1. Its velocity after 2seconds (2marks)
       2. The greatest velocity attained (2marks)
       3. The distance travelled in 10 seconds (2marks)

Marking Scheme

1.	min with = 48.35/9.375 =5.157cm max width = 48.45/ 9.365 =5.174cm absolute error = 5.174-5.157/ 2 =0.0085 %age error =0.0085/ (48.4 ÷ 9.37) ×100 =0.164%		M1 M1 A1	Alt Error in area=0.05 Error in length=0.005 R.E= %age =0.001846 error
			3
2.	1⁄2 (3x-2)(3x-7)=25 9x2×27x-36=0 x2-3x-4=0 (x+1)(x-4)=0 x=-1 or 4⇒x≠-1 x=4 Length of the base 3(4)-2=10		M1 M1 A1 B1
			4
3.	C = 180-(48+69)= 63°   a/ sin 69 = 8.4/ sin63   a=8.8 cm   b/ sin48 = 8.4/sin63 ⇒b=7cm ∴A1⁄3 × 8.8 × 7sin 63 =27.44cm2		M1 M1 A1
			3
4.	2/ 1-tan 30 = 2/ 1- 1/√3  =2√3/ √3-1  =2√3(√3+1)/ (√3-1)(√3+1)  =2√3(√3+1)/ 3-1 =6+2√3/ 2  3+√3		B1 M1 A1	Returning denominator
			3
5.	(log2x)2 + 3log2 x -10=0 let log 2 x=y y2+3y-10=0 (y-2)(y+5)=0 y=2 or -5 log2 x=2⇒x=4 log2x=-5⇒x=2-5 = 1⁄32		M1 A1 B1	Attempting to solve (y-2)(+r)=0 For For both
			3MARKS
6.	1st slab 10164×10%=1016.40 2nd slab (19740-10164)× 15⁄100=1436.40 ∴2885=1016.40+1436.40+(x-19740)× 20⁄100 0.2x=4380.20 x=sh21,901 monthly income=sh21901		M1 M1 A1	For both
			3MARKS
7.i)	E=K+C√F 22=K+C√25 28=K+C√49 K+5C=22 K+7C=28/ 2C=6 C=3 K=7		B1 B1 M1 A1	Attempt to solve Both
			3MARKS
8    .a)        b)	(1+1⁄2x)7=1+7⁄2x+21⁄4x2+35⁄8x3+35⁄16x4+21⁄32x5+7⁄64x6+1⁄28x7  x=1⁄15 ∴1+7⁄2(1⁄15)+21⁄4(1⁄15)+35⁄8(1⁄15)3 =1.25796		B1 M1 A1	CAO
			3MARKS
9.	2183= n⁄2 (10+(n-1)3) 3⁄2 n2+7⁄2 n-2183=0 3n2+72 - 4366 =0 n= n=37or-39.33 no.of terns could be-ve ∴=37		M1 M1 A1	Attempt to solve for n C.A.O
			3MARKS
10.		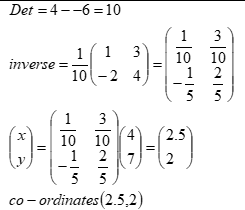	B1 M1 A1
			3MRKS
11  .a)       b)	cost of kg =2 × 650+3 × 500+5 × 420/ 2+3+5 =sh490 selling price for kg = 490 × 1.2 =588 for 3kg =588 × 3 =1764		M1 a1 M1 A1
			4MARKS
12.	4(1-sin2x)=5-4sin x 4sin2 x-4 sin x+1=0 let y = sin x 4y2 - 4y+1=0 (2y-1)(2y-1)=0 y= 1⁄2 sin x =1⁄2 x=30°, 150		m1 a1 b1
			3marks
13.i) ii)	GF=  =7.42 AG= =20.22 tan°= 7.42/ 20.22 θ=20.15°		b1 b1 m1 a1
			4marks
14.		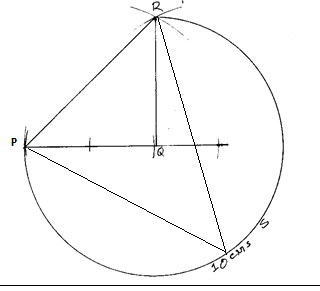	b1 b1 b1	üconstruction Of 90o forü construction of DPQR üconstruction of 450 and labelled
			3marks
15.	amplitude= 1⁄2 period= 360⁄3 =120		b1 b1	Allow
			2marks
16.	60θ=d 60θ=1920 θ= 1920/ 60 =32° longitude of =(50-32)° E =18°E		m1 a1 b1
			3marks
17   .i) ii)	750000(1 - 7⁄100)3 =750000(0.93)3 =sh603268 750000  0.933 × 0.922 × 0.893 =sh359961		m1 a1 m1 m1 a1	Alt
b)	1.22 × 359961 sh43152 ∴750000(1- r⁄1200)96 =439152 1- r⁄1200= 1 - r⁄1200 =0.9944 r⁄1200 =0.00556 r⁄12 0.556% average rate per month =6.72%		m1 m1 m1 m1 a1	For 96 indicated For root Collecting like terms
			10marks
18.a)		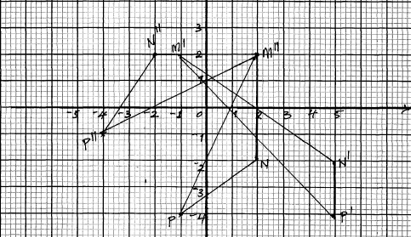	b1 b1 b1 B1	For  MNP üdrawn For M1N1 P1  location of Point üfor location of For ü  drawn
b)	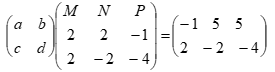2a+2b=-1 2c-2d=5 4b=-6⇒ = -3⁄2  a=1 2c+2d=2 2c-2d=-2 4d=4 d=1 c=0  matrix		m1 a1
c)	m''(2,2)N''(-2,2)P''(-4,-1)		m1 a1
d)	reflaction in the line y=x		b1 b1
			10marks
19.a)	y=-3, -7, 3		b2 B1	For allü values For two values
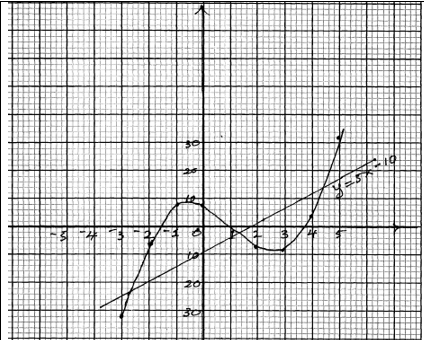			s1 p1 c1 l1	For  drawn
c)       d)	1.8, 1.0, 3.8 y=x3-3x2-5x+7 0=x3-3x2-10x+17 y=5x-10 x=-2.7, 1.4, 4.4		b1 B1 b1 B1	For y=5x-10
			10marks
20.a)	CF 1,6,14,26,33,37,39,40 Q1 =30.5 + (10-6/8)10 =35.5 Q2=50.5+(30-26/7)10 =56.21		m1 a1 m1 a1
b)	30% of 40 =12failed ∴30.5+(13-6/8)10 =30.5+8.75 pass mark = 39.25 marks		b1 m1 a1	(or 13 seen)
c)	Let the percentage be x 20.5+(x⁄100 × 40-1/ 5)10 =25 20.5+(0.4x-1)2 =25 x=3.25/ 0.4 =8.125% failed the exam (100-8.128)% passed the exam no.of student who passed 91.875/ × 100  40 =36.75 ∴37 students passed the exam		m 1 m1 a1	Alternative
			10marks
21.a)	i) CDE=70∠angle in alt segment DEC=180-130=50° DCE=180-(50+70°)=60° ∴DXE=2(DCE)=2 × 60 =120° ii) 9 × 4=12 × AD AD=3cm ∴DE=12-3=9cm iii) cos(YDE)=4.5/ 6 YDE=41.41 ADY=180-41.41 =138.59° iv) DYE=2(90-41.41)=97.18° area of segment =97.18/ 360 ×  22⁄7 × 62- 1⁄2 × 62 sin97.18 =12.68cm2 radius of section DXE = 4.5/ cos30 =5.196cm area of segment 120⁄360 × 22⁄7 × 5.1962 - 1⁄2 × 5.962 × sin120 =16.19cm2 total area of intersection =12.68+16.59 =29.27cm2		m1 a1 m1 a1 m1 a1 m1 m1 m1 a1
			10marks
22a)	2 4 2 8 2 3 5 6 4  6   8    10 5  7   9    11 7  9   11  13 8  10 12  14
i)	P(2K+t=7)= 2⁄16		b1
ii)	p(2k+t atmost p) = 9⁄16		B1
iii)	p(2k-t ≥ 0) = 12⁄16                                   t	2k   2    4    6    8 2 3 4 6 0    2    4    6 -1   1    3    5 -2    0    2   4 -4    -2   0   2	B1 B1	For table For
b)i)	x+y+z=30 x+y=15 x+z=25 =15  x=10  y=5		M1 A1	For attempting to solve all questions
ii)	p(high level cholestral only) = 15⁄40 = 1⁄4		B1
iii)	p(both) 10⁄40 = 1⁄4		B1
iv)	p(e3itherHp) = 5⁄40 + 15⁄40 = 20⁄40 = 1⁄2		M1 A1
			10marks
23.a)	x+y≥70 y≥2x 10x+15y≤1200⇒2x+3y≤240 x≥10		b1 b1 b1 b1
b)			b1 b1 b1 B1	For ü and drawn forü forü  drawn
c)i) ii iii)	2000+3000y=n For maximum point 30 of type A 60 of type B Maximum profit 30×200+3000×60 Sh240000		b1 b1 b1	Search line drawn both
			10marks
24.a)	areaA = 0∫1 (x3 4x)dx =[x4/ 4 -x2/ 2]0-1 =[1⁄4 - 1⁄2]+[0] =1⁄2 A = 1⁄2 sq units areaB = [x4/ 4 - 42/ 2]10 =[1⁄4 - 1⁄2] = 1⁄2 area= 1⁄2 total area = 1⁄2 + 1⁄2 =1sq units		m1 m1 m1 a1	forü integration for substitution of-1 and 0 for substitution
b) i)                 ii	v= ∫(30-6t)dx=30t-3t2+c 20=0+0+c c=20 v=30t-3t2+20 t=2 v=60-12+20 68cm/s 30-6t=0⇒t=5 v=30(5)-75+20 =95cm/s		m1 a1 m1 a1	(a=0)
c)	5∫0 (30t-3t2+20)dx+5 × 95 [15t2-t3+20t]50+5 × 95 350+495 =82559 sq units		m1 a1
			10marks