Mathematics Questions and Answers - Form 3 Term 1 Opener Exams 2024

1. Use tables of logarithms to evaluate; (3 marks)
   
2. The length, width and height of cuboid of mass 40g, are 10 cm, 5 cm and h cm respectively. If it has a density of 0.02g/cm³, calculate the height of the Cuboid. (3 marks)
3. A man walks directly from point Q towards the foot of a vertical flag post 200 m away, after covering a distance of 140m , he observes the angle of elevation of the top of the flag post is 75°. Calculate to 2 decimal places
   1. The height of the flag post (2 marks)
   2. The angle of elevation from point Q to the top of the flag post (2 marks)
4. Without using mathematical tables or calculator evaluate (3 marks)
   27.72 × 0.3876
    2.09 × 0.4284
5. Evaluate  <sect/li>
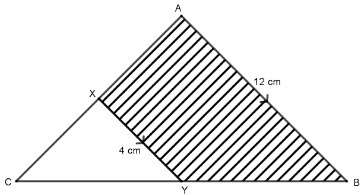
6. In the figure below lines AB and XY are parallel AB = 12 cm and XY= 4 cm
   
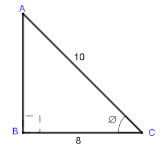
   If the area of the shaded region is 36cm² .Find the area of the triangle CXY (3 marks)
7. Given that cos θ = ⁸/₁₀ , without using mathematical tables express in fraction form the value of
   1. sin θ (2 marks)
   2. tan (90 − θ) (1 mark)
8. Given that P = 5ǎ-2b̌ where ǎ=3 2 and b̌=4 1 .Find:
   1. Column vector P. (2 marks)
   2. P' the image of P under a translation vector (−6 4) . (1 mark)
9. Simplify (3marks)
   3x² − 4xy + y² 
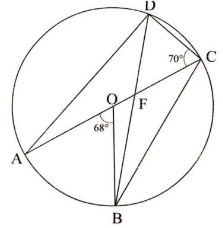
        9x² − y²
10. The figure below shows a circle centre O and AOC as its diameter .Chords BD and AC intersect at F . Given that angle AOB=68° and angle ACD=70°.
    
    Find the size of
    1. Angle DAC (1 mark)
    2. Angle BFC (2 marks)
11. Find the value of x in the equation 81^x × ¹/₃ × 9^2x + 74 = 317 (3 marks)
12. Find the surface area of a cone whose diameter is 12cm and height 8cm (3 marks)
13. Three automatic electric bells A, B and C ring at intervals of 20 minutes, 30 minutes and 50 minutes respectively. If the bells ring together at 8.20 a.m, at what time will they ring simultaneously again for the first time. (3 marks)
14. The equation of a line is −³/₅x + 3y = 6
    Find the:
    1. Gradient of the line. (1 mark)
    2. Equation of a line passing through point (1, 2) and perperndicular to the given line. (2 marks)
15. The area of a rhombus is 60cm² .If the shorter diagonal is 8cm ,Find the perimeter of the rhombus (4 marks)
16. State all the integral values of x that satisfy the following inequality. (3 marks)
    2x−3 ≤ 3x+5 ≥ 7x+6

SECTION II (50 marks)
Attempt ALL questions in the spaces provided in this section

17. The diagram below represents two vertical watch towers RS and TU on a level ground. P and Q are two points on a straight road SU. The height of the tower RS is 20 m and road SU is 200m.
    
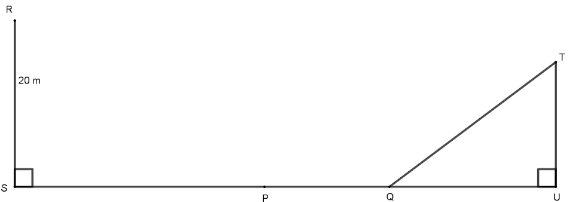
    1. A bus moves from S towards U. At point P, the angle of depression of the bus from point R is 11.3°. Calculate the distance SP to 4 significant figures. (2 marks)
    2. If the bus takes 5 seconds to move from P to Q at an average speed of 36 km/h, calculate the angle of depression of Q from R to 1 decimal place. (3 marks)
    3. Given that QT = 50.9 m, calculate;
       1. The height of TU in metres to 1 decimal place. (2 marks)
       2. The angle of elevation of R from T to the nearest degree. (3 marks)
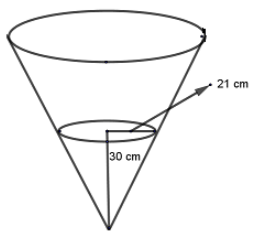
18. The diagram below represents a conical vessel which stands vertically .The vessel contains water to a depth of 30cm .The radius of the surface with water in the vessel is 21cm .(Take π = ²²/₇)l
    
    1. Calculate the volume of the water in the vessel in cm³ (3 marks)
    2. When a metal sphere is completely submerged in the water ,the level of water in the vessel rises by 6cm.Calculate
       1. The radius of the new water surface in the vessel (2 marks)
       2. The volume of the metal sphere in cm3 (3 marks)
       3. The radius of the sphere (2 marks)
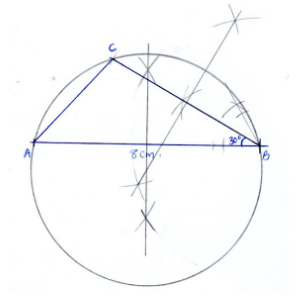
19. Using a pair of compasses and ruler only;
    1. Construct triangle ABC such that AB = 8cm, BC = 6cm and angle ABC = 30°. (3 marks)
    2. Measure the length of AC (1 mark)
    3. Draw a circle that touches the vertices A,B and C. (2 marks)
    4. Measure the radius of the circle (1 mark)
    5. Hence or otherwise, calculate the area of the circle outside the triangle. (3 marks)
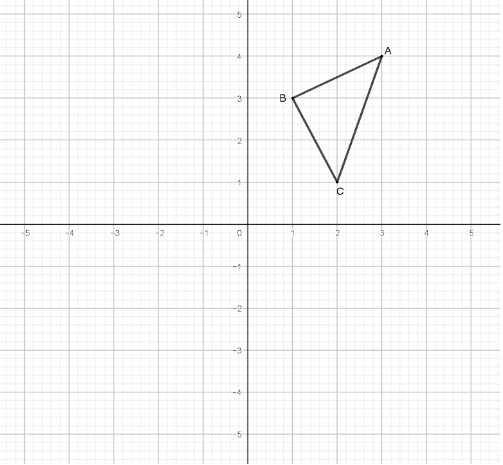
20. The diagram below shows triangle ABC with A3, 4, B(1, 3) and C(2,1).
    
    1. Draw ∆A'B'C' the image of ∆ABC under a rotation of +90° about 0, 0. (2 marks)
    2. Draw ∆A''B''C'' the image of ∆A'B'C' under a reflection in the line y−x=0. (2 marks)
    3. Draw ∆A'''B'''C''' the image of ∆A''B''C'' under a rotation of −90° about 0, 0(2 marks)
    4. State the coordinates of triangles ∆A''B''C'' and ∆A'''B'''C'''. (2 marks)
    5. Write down the equation of the lines of symmetry of the quadrilateral ''A'''A' . (2 marks)
21. The mass in kilograms of 30 patients who attended a clinic on a certain day were recorded as follows:
    

    38	52	46	60	39	62	73	49	54	49
    41	57	58	79	62	58	54	65	56	69
    72	58	42	41	67	49	51	54	59	60

    1. Starting with a class width of 35-39 ...make a frequency distribution table for the data indicating the class and frequency (3 marks)
    2. State the modal class (1 mark)
    3. Calculate the median mark (3 marks)
    4. Calculate the median mark (3 marks)

MARKING SCHEME

No	Working	Marks
1.		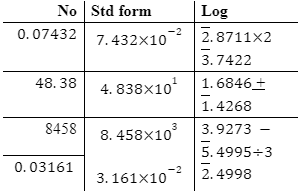M1 all correct logs M1 addition, subtraction, cube root  A1 answer
2.	Volume =   40   = 2 000 cm³                  0.02 2 000=10×5×h h =  2 000   =  40 cm       (10×5)	M1  M1  A1
3.	Tan 75⁰ = h/140 h = 140 tan 75    = 522.99m tan θ = 522.99                200           =72.83⁰	M1  M1  A1
4.	2772×3876  209×4284 = 12	M1  M1  A1
5.		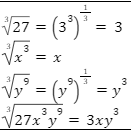M1    A1
6.	L.S.F = 4/12 = ¹/₃, A.S.F =¹/₉ ¹/₉ = x/(x+36) 9x − x = 36 x = 4.5cm²	M1  M1   A1
7.	AB= √(10² − 8²) = 6 sin θ = 6/10  tan (90 − θ) = ⁸/₆ = 4/3	M1  A1  B1
8.	P = 5(3 2) −2(4 1 )    = (7 8) (7 8) + (−6 4) = (1 12)	M1  A1  B1
9.	N = 3x²−3xy−xy+y² (3x−y)(x−y) D=(3x−y)(3x+y)   (3x−y)(x−y)    3(x−y)(3x+y)   x−y   3x+y	B1  B1  A1
10.	Angle DAC = 90-70=20° Angle BFC = 180-20+34 = 126°	B1  M1  A1
11.	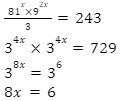x = ³/₄	M1  M1  A1
12.	L = √(6²+ 8²) = 10 cm TSA = (²²/₇ × 6 × 6) + (²²/₇ × 6 × 10)         = 113.14 + 188.57 = 301.71cm²	B1  M1  A1
13.	LCM of 20, 30 and 50 = 300 Time taken = 300 minutes = 5 hours Next time of ringing = 8.20 a.m + 5 hrs = 1.20 p.m same day	M1  A1  B1
14.	y=¹/₅x+2 Gradient = ¹/₅ −5/1 = (y−2)           (x−1) −5(x−1) = y−2 y = −5x+7	B1  M1  A1
15	A =¹/₂ × product of diagnols 60 =¹/₂ × 8 × x x=15cm 4² + 7.5² = l² √75.25=l    = 8.5cm p = 8.5 × 4 = 34 cm	B1  M1 A1
16.	2x−3 ≤ 3x+5 x ≥ −8 3x+5 ≥ 7x+6 x ≤ −0.25 Integral values are ⟹ −8, −7, −6, −5, −4, −3, −2 and −1	M1  M1  A1
17.	tan 11.3 = 20/SP SP =      20      =100.1 m          tan11.3 PQ = 5×10=50 m tan θ =    20                 150.1  θ =    20   = 7.6°       150.1   QU=200-150.1 = 49.9 m TU = TU=10.0 m tan β = 10/200 β = (10/200) = 3°	M1  A1  M1  M1 A1  M1  A1  M1  M1A1
18.	Volume = 1/3 × 22/7 ×212 × 30 = 13860cm3   30/36 = 21/R = 21×36                         30 =25.2cm new volume = 1/3 × 22/7 ×25.22 × 30 = 23950.08cm3 volume of sphere = 23950.08 − 13860                               = 10090.08cm3 10090.08 = - × r3               r3 = 10090.08 × 7/22 × 3/4  r = 3√(2407.86) r = 13.40cm	M1B1  A1  M1  A1  B1  M1  A1  M1  B1  A1
19	AC = 4.1 ± 0.1cm On the diagram Radius 4.1 ± 0.1cm Area of circle = 22/7 × 4.1 × 4.1 = 52.83cm2 Area of ΔABC = 0.5 × 8 × 6 × sin 30° = 12cm2 Difference = 52. 83 − 12 = 40.83cm2	B1 – lines AB,BC B1 - ∠ABC B1 – complete triangle B1 B2 B1 M1 M1A1
20.	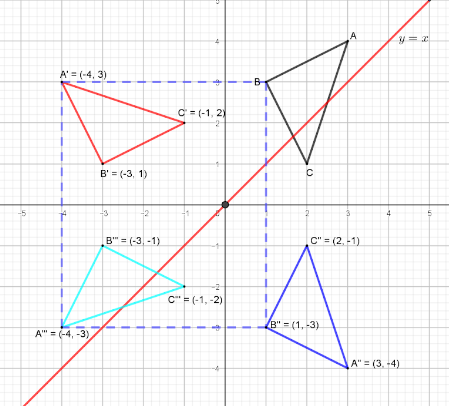(e) y = 0 and x = −1.5	B1B1
21	Marks  frequency   Midpoint(x)   fx   cf   35-39  2  37  74  2  40-44  3  42  126  5  45-49  4  47  188  9  50-54  5  52  260  14  55-59  6  57  342  20  60-64  4  62  248  24  65-69  6  67  201  27  70-74  2  72  144  29  75-79  1  77  77  30    Σf = 30    Σfx = 1660   55-59 mean = 1660 = 55.33                 30 median = 54.5 + (15 −14) × 5                                  6             = 54.5 + 0.8333             = 55.33	B1 for fx  B1 for f  B1 for classess  Correct Σfx B1            B1  M1 A1  M1  M1  A1