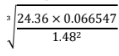Mathematics Paper 2 Questions - Kapsabet Boys Post Mock 2023 Exams

Instructions to candidates

• The paper contains two sections: Section I and Section II.
• Answer ALL the questions in Section I and ANY FIVE questions from Section II. 
• All working and answers must be written on the question paper in the spaces provided below each question.
• Marks may be awarded for correct working even if the answer is wrong.
• Negligent and slovenly work will be penalized.
• Non-programmable silent electronic calculators and mathematical tables are allowed for use.

1. Use Logarithms correct to four significant figures to evaluate. (4marks)
   
2.  
   1. Expand and simplify (½x − ¹/₃y)⁴   (2marks)
   2. Hence evaluate (¹/_√2 − ¹/_√3)⁴ leaving your answer in surd form (2marks)
3. A mixture is made by mixing 4kg of long grain rice costing sh 60 per kg with 9kg of short grain rice costing sh 50 per kg. How many kilograms of long grain rice should be added to the mixture so that the resulting mixture can be sold at sh 66 per kg and a profit of 20% is made. (3marks)
4. Find the centre and radius of a circle whose equation is shown below (3marks)
   2x² + 2y² −12y−14 = 0
5. Peter invested a certain amount of money in a financial institution at compound interest compounded quarterly. At the end of the third year it had amounted to sh 18980 and by the end of the fifth year it had amounted to sh 20530. Find the rate of interest   (4marks)
6. A point C divides the line AB with coordinates A (3, 4 ,−5) , B (−1,10,7) externally in the ratio 5 : 3. Find the coordinates of C (3marks)
7. A and B are points on latitude 70°N.Their longitudes are 62°W and 118°E respectively. Find the shortest distance between A and B in nautical miles. (2marks)
8. Estimate the area enclosed by the curve y =   1   and the x axis from x = 0 to x = 2 using mid ordinate rule with four strips. (Leave your answer as a fraction).   (3marks)                               4x+1
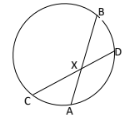
9. In the figure below AB and CD are chords intersecting internally at point X. If CD = 6.5cm, CX = 2.5cm and BX = 2.2 cm Calculate the length of AX.   (2marks) 
   
10. Calculate the standard deviation of the given data (3marks)
    3, 7, 2, 1, 8, 9, 13, 6, 4, 7
11. Make C the subject of a formula in the equation (3marks)
    
12. The forth term of a geometric sequence is 48 and the seventh term is 384.Find the common ratio and the ninth term of the sequence. (3marks)
13. The masses of two objects to the nearest 100g are 51kg, and 43kg find the percentage error in the difference of their masses. (3marks)
14. Solve the equation 9tan²θ + tanθ = 10 for 0° ≤ θ ≤ 360° (4marks)
15. The volume V of a cylinder varies jointly as the square of the radius R and the height H. If the radius is increased by 10% and the height decreased by 20%find the percentage change in the volume. (3marks)
16.  
    1. Determine the inverse of the matrix T = (1mark)
    2. Hence find the co-ordinates of the point of intersection of the lines whose equation are x + 2y= 7 and  x − y = 1 (2marks)

SECTION II - (50 MARKS)

Answer ONLY five questions

17.  
    1. AB and CD are chords of a circle Construct the circle with centre O and measure its radius (4marks)
       
    2. Construct the loci of a points x which are equidistant from line AB and CD (1mark)
    3. locate the loci of a points Y which are equidistant from points C and D (1mark)
    4. Construct the loci of a points Z which are 2cm from the circumference of the circle. (1marks) 
    5. A point P moves such that CP ≥ DP, It is not more than 2cm from the circumference of the circle and its distance from line CD is not more than its distance from AB. Show the region P by shading it. (3marks)
18.  
    1. Complete the table below, giving values correct to two decimal places. (2marks)
       

       x°	0	15	30	45	60	75	90	105	120	135	150	165	180
       Tan x°
       2 Sin2x° − 2

    2. Draw the graph of y = tanx° and y = 2sin2x° − 2 (4marks)
    3. From your graph state the amplitude and period of y = 2sin2x° − 2 (1mark)
    4. Use your graph to solve the equation (2marks)
       1. ½tanx° + 1 = Sin2x°
       2. Sin2x° = 0
19. In order to ensure optimal health a lab technician needs to feed the rabbits on a daily diet containing a minimum of 24grams of fat, 36grams of carbohydrates and 4grams of protein. Rather than order rabbit food that is custom blended it is cheaper to order food X and food Y and blend them for an optimal use. One packet of food X contains 6grams of fat ,12 grams of carbohydrates ,2 grams of proteins and costs Sh 50.While one packet of food Y contains 12grams of fat,12 grams of carbohydrates,1 gram of proteins and it costs
    1. Form all the inequalities to represent the information above. (4marks)
    2. Graph the inequalities (4marks)
    3. Determine the number of packets of type X and Y feed that should be used for optimal health at minimum cost. (2marks)
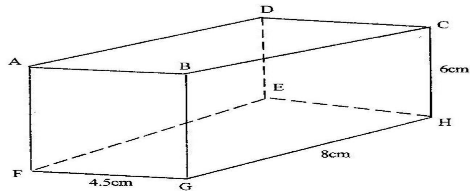
20. The diagram below represents a cuboid ABCDEFGH in which FG= 4.5 cm, GH=8cm and HC=6 cm.
    
    Calculate:
    1. The length of FC (2 marks)
    2.  
       1. The size of the angle between the lines FC and FH (2 marks)
       2. The size of the angle between the lines AB and FH (3 marks)
       3. The size of the angle between the planes ABHE and the plane FGHE (3 marks)
21. At the Kenya medical research institute a new drug is being tried. A sample of eighty sick rats is being used. Sixty of these rats are given drugs and the rest are not. A half of those given drugs are put on a high calorie diet while three quarters of those who are not given drugs were put on the same diet. For the ones who are treated and put on a high calorie diet the probability of dying is 0.1 and 0.2 if not put on a high calorie diet. For the ones who are not treated and put on a high calorie diet the probability of dying is 0.4 and 0.6 if not put on a high calorie diet.
    1. Draw a tree diagram to represent the above information. (2marks)
    2. Calculate the probability that a rat picked at random
       1. Is given drugs, put on a high calorie diet and will die (1mark) 
       2. Is given drugs and will die . (2marks)
       3. Will die (3marks)
       4. Is not given drugs and will not die (2marks)
22. The table below shows the rate at which income tax was charged for all income earned in the year 2012.
    

    Taxable income per month in k£	Rate of tax per k£
    1 = 236	10%
    237 - 472	15%
    473 - 708	20%
    709 - 944	25%
    945 and above	30%

    1. A tax of ksh1200 was deducted from Mr. Rono’s monthly salary. He was entitled to a personal relief of ksh 1064 per month. Calculate his monthly
       1. Gross tax in k£. (1mark)
       2. Taxable income in ksh.   (5marks)
    2. He was entitled to a house allowance of ksh 3000 and medical allowances of ksh 2000 calculate his monthly basic salary in ksh. (1mark)
    3. Every month the following deductions were made from his salary electricity bill of sh 680, water bill of sh 460, co-operative shares of sh1250 and loan repayment of sh 2000 calculate his net salary in ksh. (3marks)
23. A particle is moving with an acceleration of (t – 4) m/s2where t is time in seconds. When t is 2 seconds the velocity is 4m/s and when t is 0 the displacement is 0m
    1. Express velocity in terms of t (2marks)
    2. Find the displacement of the particle during the third second. (2marks)
    3. Calculate the interval of time when the velocity was not more than 4m/s   (3marks)
    4. Calculate the minimum velocity. (3marks)
24. In the figure below O is the center of the circle and ABCDEA is a regular polygon inscribed in a circle. Line GEF is a tangent to the circle at point E.
    
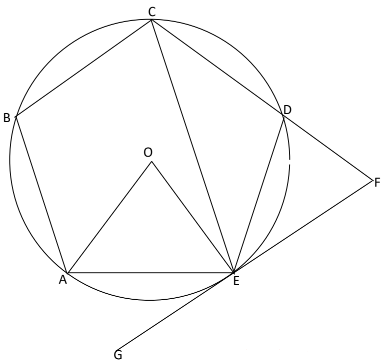
    1. Find angle
       1. AEG (1marks)
       2. OEC (2marks)
       3. DFE (2marks)
       4. Obtuse angle AOC (2marks)
    2. If the sides of the pentagon are 6cm find the area of the circle giving your answer to one decimal place (3marks)