Mathematics Questions and Answers - Grade 5 End Term 2 Exams 2023 Set 1

1. The number of registered voters in a certain couny is 78483. What is the number of people written in words?
   1. Seventy eight thousand four hundred and eighty four
   2. Seven hundred and eighty four thousand four hundred and three
   3. Seven thousand four hundred and eighty three
   4. Seventy eight thousand four hundred and eighty three
2. What is the place value of digit 9 in the number 597624?
   1. Hundreds
   2. Tens of thousands
   3. Thousands
   4. Hundreds of thousands
3. In the year 2022, a total of 390768 passengers travelled by train. What is the total value of digit 0?
   1.  Thousands
   2. 1000
   3. 0
   4. 90000
4. Kericho tea factory sold the following amount of tea leaves in a given month.
   
   

   Week 1	week 2	week 3	week 4
   29500kgs	81760kgs	59605kgs	18607kgs

   
   Arrange the mass of the tea leaves in a decreasing order
   1. 81760, 59605, 18607, 29500
   2. 18607, 29500, 59605, 81760
   3. 81760, 18607, 59605, 29500
   4. 81760, 59605, 29500, 18607
5. Roy spent sh. 25678 to buy a television set. How much did he spend on the television set to the nearest thousands?
   1. 25000
   2. 25700
   3. 26000
   4. 30000
6. Which of these sets of numbers is divisible by 10?
   1. 468, 800, 2010, 17000
   2. 1275, 550, 110, 560
   3. 17575, 4800, 50, 900
   4. 24400, 2500, 4320, 1600
7. Work out:
               62.304
            – 41.009
           _______
   
   
   1. 21.295
   2. 21.205
   3. 21.205
   4. 20.295
8. How many ¼ kgs are there in 24kgs of rice?
   1. 96
   2. 24
   3. 20
   4. 6
9. Write this fraction in its simplest form, ⁴⁸/₈₄
   1. ²⁴/₄₂
   2. ¹²/₂₁
   3. ⁷/⁴²
   4. ⁴/₇
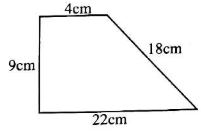
10. Work out the perimeter of the figure below
    
              
    1. 130cm
    2. 49cm
    3. 53cm
    4. 89cm
11. What is the place value of digit 6 in the number 14.396?\
    1. Hundredths
    2. Tenths
    3. Hundreds
    4. Thousandths
12. Atieno bought maize flour in bags of 150kg and 100kg. What is the greatest mass of maize that can be measured equally from each of the bags without a remainder?
    1. 100
    2. 150
    3. 50
    4. 250
13. Karura forest has 120416 trees, Ngong forest has 41222 trees while Nyabene forest has 227634 trees. How many trees do the three forests have altogether?
    1. 398272
    2. 388262
    3. 161638
    4. 389272
14. Mr. Musa shared 269 Science and Technology textbooks equally among 18 learners. How many books remained after sharing?
    1. 14
    2. 17
    3. 24
    4. 16
15. Fill in the missing number
    
    ³/₇ = /₁₄
    
    1. 6
    2. 12
    3. 9
    4. 10
16. Jayden wakes up in the morning at the time shown by the digital clock below.
                             
    1. 6.45pm
    2. 6.15am
    3. 6.15pm
    4. 6.45am

Below is a price list. Use it to answer questions 17 and 18

1. Vanessa bought 2 litres of cooking oil and a packet of milk. She gave the shopkeeper sh. 1000. How much balance did she get?
   1. sh. 399
   2. sh. 301
   3. sh. 299
   4. sh. 209
2. How much did Owaro pay after buying 2kg of maize flour and a loaf of bread?
   1. sh. 303
   2. sh. 293
   3. sh. 135
   4. sh. 259
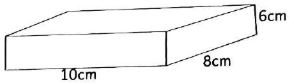
3. Work out the volume of the figure below
   
   
   
   1. 480cm³
   2. 480cm³
   3. 480cm³
   4. 480m³
4. Delmonte Company processed 2540 litres of pineapple juice. A trader bought 995 litres of the pineapple juice. How many litres of the juice remained?
   1. 1645L
   2. 1655L
   3. 1745L
   4. 1545L
5. It takes 3 weeks for eggs to hatch. How long is this period in days?
   1. 28 days
   2. 21 days
   3. 14 days
   4. 18 days
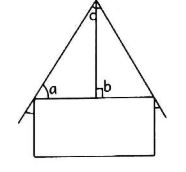
6. The diagram below shows a roof of a house. Write the type of the angle marked b.
             
   1. Obtuse angle
   2. Acute angle
   3. Reflex angle
   4. Right angle
7. Complete the pattern below. 80, 76, 72, ___,___, 60
   1. 68, 64
   2. 73, 74
   3. 64, 68
   4. 74, 76
8. A farmer harvested n bags of beans, p bags of rice and 2w bags of millet. How many bags did she harvest altogether?
   1. b+r+2w
   2. n -p -2w
   3. n + p+ 2w
   4. n + p-2w
9. Work out the following
                         H                 Min
                         8                   30
                       - 6                   55
                      ______________
   
   
   1. 1 hr 75 min
   2. 2h 25 min
   3. 1h 35 min
   4. 2 h 35 min
10. A parking lot has 14 pick-ups. Each pick-up is charged sh. 212 per day. How much money is collected from the parking lot in a day?
    1. shs. 288
    2. shs. 2968
    3. shs. 2568
    4. sh. 2768
11. Which statement can correctly fill the blank space below?
    
                         ²/₃ is __________ ⁸/₁₂
    1. greater than
    2. less than
    3. equal to
    4. larger than
12. Work out:
    12km 600m x 6 = ______
    1. 72km 600m
    2. 74km 600m
    3. 75m 800m
    4. 75km 600m

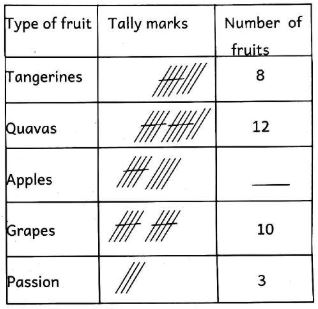
The table below shows the number of fruits sold by a vendor in a day in Gikomba market. Use it to answer questions 29-30

1. Which fruit had the least number of sales?
   1. Quavas
   2. Passion
   3. Tangerines
   4. Apples
2. How many fruits in total did the vendor sell?
   1. 40
   2. 39
   3. 42
   4. 41

MARKING SCHEME

1. D
2. B
3. C
4. D
5. C
6. D
7. A
8. A
9. D
10. C
11. D
12. C
13. D
14. B
15. A
16. D
17. C
18. A
19. C
20. D
21. B
22. D
23. A
24. C
25. C
26. B
27. C
28. D
29. B
30. C