Measurements - Class 8 Mathematics Revision Notes

Length, Perimeter and Area

Worked Exercise

1. Tracy used a piece of wire m long to support tomato plants in the garden. The wire was cut into pieces of 28cm long. How many complete pieces were obtained?
   1. 85
   2. 30
   3. 20
   4. 30.10
      Working
      1 M = 100cm
      8½m = ?
      8½ x 100 = 850cm
      1 piece = 28 cm
                ? = 850cm
      = ⁸⁵⁰/₂₈
      = 30 complete pieces remainder 10cm
2. The figure below represents a flower garden
   
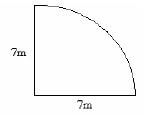
   What is the perimeter of the garden?
   1. 25m
   2. 38.5m
   3. 11m
   4. 44m
      Working
      P = ¼П d + r + r
      = ( ¼ x ²²/₇ x 14) + (7+7)
      = 11 + 14
      = 25 m
      The correct answer is A (25)
3. The parallel sides of a trapezium measure 10cm by 18cm respectively. If the distance between the parallel sides is 8cm, what is the area of the trapezium in cm²?
   1. 224
   2. 112
   3. 108
   4. 84
      Working
      Area of a trapezium = ½h (a + b)
      = ½ x 8 x (10+18)
      = ½ x 8 x 28
      = 112cm²
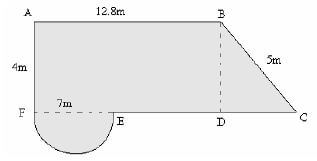
4. The figure below shows vegetable garden.
   
   What is the perimeter?
   1. 0.526m
   2. 5.26m
   3. 52.6m
   4. 526m
      Working
      Perimeter of semi-circle
      = ½П d(Circumference only)
      =½ x 2 x ²²/₇ x 7
      = 22m
      To get DC = √ 25 – √ 16
      = √ 9
      = 3m
      Length DE = AB – ED
      = 12.8 – 7
      = 5.8m
      Total length 12.8+ 5 + 3 + 5.8 + 22 + 4
      = 52.6 m
      The correct answer is (52.6)
5. What is the perimeter of the following shape?
   
   
   1. 88cm
   2. 44cm
   3. 176cm
   4. 56cm
      Working
      P = circumference of a circle of radius 7cm
      = 2Π r
      = 2 x ²²/₇ x 7
      = (44 cm)
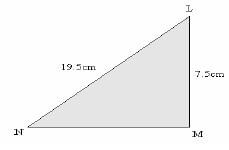
6. The figure below shows a right angled triangle LMN in which LM = 7.5cm and LN = 19.5cm
   
   What is the area of the triangle in cm²?
   
   1. 18
   2. 67.5
   3. 27
   4. 34.5
      Working
      Apply Pythagoras relation in triangle LMN
      LN² = LM² + NM²
      Nm² = LN² – LN²
      = 19.5² – 7.5²
      = 380.25 – 56.25
      = 324
      NM = √ 324
      = 18 cm
      Area of triangle LMN
      = Base x height
      = ½ X 18 X 7.5
      = 67.5cm²
      The correct answer is B (67.5cm²)
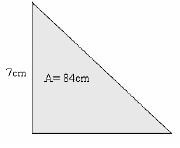
7. The area of a right-angled triangle is 84cm². If the height of the triangle is 7cm, what is the length of the longest side?
   1. 25cm
   2. 24cm 
   3. 19cm
   4. 12cm
      Working
      
      The Pythagoras relationship states that
      H² = b² + h²
      But Area = ½bh
      84 =½ x b x 7
      84 x 2 = 7b
      24 = b
      H² = 24² + 7²
      H² = 576 + 49
      H² = 625
      H = 25
      Therefore the correct answer is 25cm (A)
8. What is the surface area of an open cylinder whose radius is 6.3cm and height of 25cm.
   1. 114.74cm²
   2. 1239.48cm²
   3. 3118.50cm²
   4. 619cm²
      Working
      Total surface area = Πr²+Πdh
      = ( ²²/₇x 6.3 x 6.3) + 2 x ²²/₇ x 6.3 x 25
      = 124.74 + 990
      = 1114.74 cm²
      The correct answer is 1114.74 cm² (A)
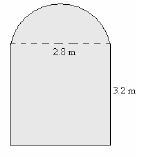
9. A Welder made a door with a design as shown below.
   
   What is its area? (Take Π =²²/₇ )
   1. 15.12m²
   2. 12.04m²
   3. 13.36m²
   4. 21.28m²
      Working
      Area of the semi- circle = ½Π r²
      = ½ x ²²/₇ x 1.4 x 1.4
      = 3.08m²
      Area of the rectangle = L x w
      = 3.2 x 2.8
      = 8.96 m²
      Total area = (3.08 + 8.96 )m²
      = 12.04 m²
      The correct answer is B (12.04m²)
10. The diagram below represents a plot with a diameter of 28 meters.
    
    The plot was fenced by erecting posts 4m apart. How many posts were used ? (Π = ²²/₇)
    1. 12
    2. 17
    3. 18
    4. 19
       Working
       Perimeter =½ П d + d
       = (½ x ²²/₇ x 28 + 28)
       = 72
       No of posts = ^Perimeter/_Interval
       =⁷²/₄
       = 18 posts
       The correct answer is C (18)