Geometry - Class 8 Mathematics Revision Notes

Geometry

Worked Exercise

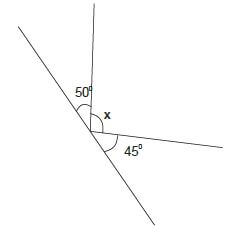
1. Find the value of x in the following.
   
   Working
   X+45+50=1800 (Angles on a straight lines are supplementary i.e. add up to 180º )
   X+95=180º
   X=85º
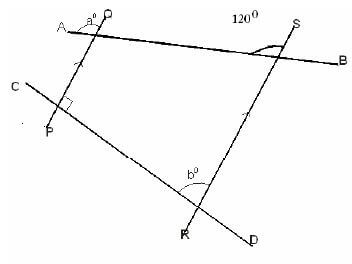
   The value of x =85º
2. Find the sum of angle “a” and angle “b” in the figure below.
   
   Working
   Lines AB and C D are transversals  are Therefore 90+b = 1800
   Co-interior angles - supplementally
   Therefore b=180-90
   B = 90º
   Angle a = 120º - (Corresponding angles)
   Therefore a = 120º
   Sum of a and b
   =120 + 90
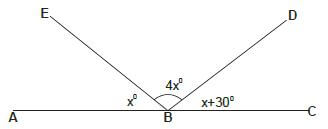
   = 210º
3. Find the size of angle marked A B D in the figure below.
   
   X+4x+x+30=180º (angles on a straight line are supplementary)
   = 6x+30=180
   6x=180-30
   6x = 150
   X = 25
   Angle A B D =x + 4X
   But x = 25
   Therefore 25 + (4 x 25)
   = 25 + 100
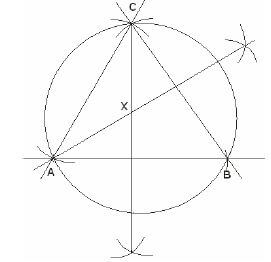
   = 125º
4. Draw an equilateral triangle A B C where Line AB = 6cm.
   Draw a circle touching the 3 vertices of the triangle. What is the radius of the circle?
   Working
   Steps:
   1. Draw line A B = 6cm
   2. With A as the Centre with the same radius 6cm, mark off an arc above line A B.
   3. With B as the Centre with the same radius 6cm, mark off an arc above line A B to meet the arc in (II) above. Call the point of intersection point C
   4. Join C to A and C to B
   5.  Bisect line A B and B C and let the bisectors meet at point X.
   6. With X as the Centre, draw a circle passing through points A, B and C.
   7. Measure the radius of the circle.
      
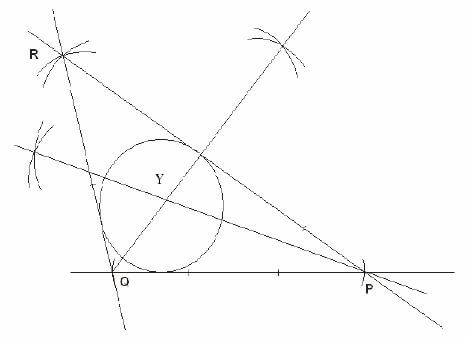
5. Construct a triangle P Q R in which Q P = 6cm. Q R = 4cm and P R =8cm. Draw a circle that touches the 3 sides of the triangle, measure the radius of the circle.
   Working
   1. Draw line Q P 6cm
   2. With Centre Q, make an arc 4cm above line Q P.
   3. With Centre P, make an arc 8cm above line Q P and let the arc meet the one in (II) above. Label the point of intersection as R.
   4. Join R to P and R to Q.
   5. Bisect any two angles and let the bisectors meet at point Y.
   6. With Y as the Centre, draw a circle that touches the 3 sides of the triangle.
      
      Construction
      R = 3.5cm
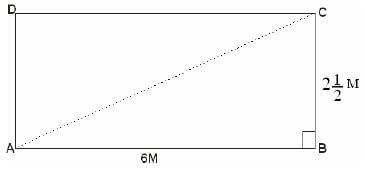
6. A rectangle measures 6cm by 2½ cm. What is the length of the diagonal?
   Working
   
   AC² = AB² + BC² [ Pythagoras Theorem]
   AC² = 6² + 2 ½²
   AC² = 36 + 6.25
   AC² = 42.25
   AC = √42.25
   = 6.5 or 6 ½
   NB: The Pythagoras theorem states
   H² =B² +h²
   h² = H² – b²
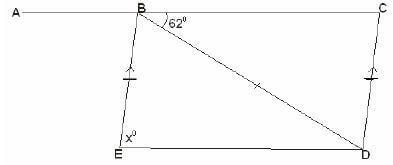
   b² = H² –h²
7. In the figure below, A B C is a straight line and B C D E is a quadrilateral. Angle CBD = 620 and lines EB = BD = DC. Line EB is parallel to DC.
   
   What is the size of angle BDE?
   Working
   Consider triangle BCD (isosceles triangle)
   Therefore base angles are equal
   CBD = 62º
   BCD = 62º
   Therefore, BDC = 180 – 124 = 56º
   Angle CDB = angle EBD [Alternate triangle]
   Therefore EBD = 56º
   Angle BDE =^{180 - 56}/₂
   = 62º
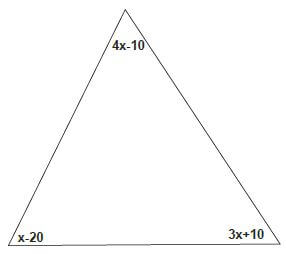
   Therefore, BDE = 62º
8. Find the size of the largest angle from the following triangle.
   
   Working
   4X – 10 + x – 20 + 3x + 10 = 180 [Angle sum of a triangle]
   8x – 20 = 180
   8x = 200
   X = 25
   4x – 10 = (100 – 10)º
   = 90º largest angle.