- Kinetic Particle Theory
- Diffusion and Kinetic Energy
- Evaporation, Boiling and Kinetic Theory
- Kinetic Theory and Gas Laws
- Gases and the Kinetic Theory

Kinetic Particle Theory
- Matter is made up of particles that are in constant motion
- The higher the temperature, the faster the particles move (more energy)
- Increase in temperature increase weakens interparticle forces, causing particles to spread apart and increase in volume/size (i.e. Expansion)
- Gases have greatest average energy while solids have smallest average energy
According to the kinetic theory, matter is made up of particles (atoms, molecules or ions) which are in constant motion because they have energy at all temperatures above zero Kelvin (absolute zero, 0K) or -2730C. This energy is in the form of kinetic energy.
Consider heating a solid;
- When a solid is heated, the particles vibrate more strongly as they gain kinetic energy and the particle attractive forces are weakened.
- Eventually, at the melting point, the attractive forces are too weak to hold the particles in the structure together in an ordered way and so the solid melts.
- The particles become free to move around and lose their ordered arrangement. Energy is needed to overcome the attractive forces and give the particles increased kinetic energy of vibration.
- On heating further, the particles gain more kinetic energy and move faster. In evaporation and boiling the particles with the highest kinetic energy can ‘escape’ from the attractive forces of the other liquid particles.
- The particles lose any order and become completely free to form a gas or vapour.
- Boiling is rapid evaporation anywhere in the bulk liquid and at a fixed temperature called the boiling point and requires continuous addition of heat.

Diffusion and Kinetic Energy
- The natural rapid and random movement of the particles means that gases readily ‘spread’ or diffuse.
- Diffusion is the movement of gas or solid particles from a region of high concentration to a region of low concentration.
- Diffusion is fastest in gases where there is more space for them to move. The rate of diffusion increases with increase in temperature as the particles gain kinetic energy and move faster.
Diffusion of Ammonia and Hydrogen Chloride
- The following experiment is set up. One filter soaked in a solution of ammonia solution and the other soaked in a solution of concentrated hydrochloric acid are placed on the end of along glass tubing as shown.
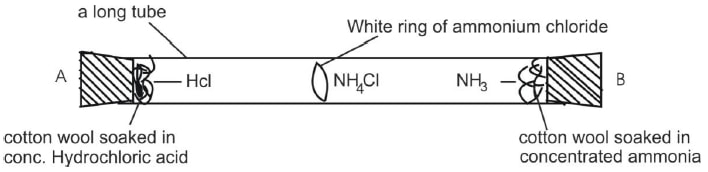
- When colourless NH3 and HCl fumes meet, dense white smoke (fumes) of ammonium chloride are observed.
NH3 (ag) + HCl (ag) → NH4Cl (s) - Ammonia is diffused more rapidly than the hydrogen chloride because the gas traveled a longer distance in the same amount of time.
- Gases with greater R.M.M have higher densities than gases which have small molecules e.g. hydrogen chloride are heavier than ammonia molecules.
- If the concentration of hydrochloric acid and that of ammonia were increased in a separate experiment, the rate of diffusion would be faster.
Gas Mass NH3 17 HCl 35.5 - Large heavy molecules move more slowly than small, light molecules. Therefore, dense gases diffuse more slowly than gases of low density.
- The rate of diffusion depends on the molecular mass/density of gas. Rate of diffusion is inversely proportional to mass of a gas.
RATE OF DIFFUSION;
- Increases with temperature
- Decreases with increasing R.M.M or R.A.M
- Increases with concentration
Graham’s Law of Diffusion
- Graham’s law of diffusion relates the rate of diffusion of a gas to its density.
- It states that the rate of diffusion of a gas at constant temperature and pressure is inversely proportional to the square root of its density.
Rate of diffusion ∝ 1/√density - If two gases A and B diffuse under the same conditions of temperature and pressure, then
Rate of diffusion of A = √density of B
Rate of diffusion of B √density of A - The density of a gas is proportional to its molecular mass.
- Hence, rate of diffusion of a gas ∝ 1 /√Molecular mass
Or
Rate of diffusion of A = molecular mass of B
Rate of diffusion of B molecular mass of A - For equal volume of gas, rate of diffusion ∝ 1/Time of diffusion
Example 1: Rates of diffusion of two gases A and B are in the ratio 2:1. If the molecular mass of gas of A is 16g, find the molecular mass of B.
Rate of diffusion of A = √mol. Mass of B
Rate of diffusion of B √mol. Mass of A
2 = √M
1 √16
√M = 2 x √16 = 8, hence M = 82 = 64
Molecular mass of B = 64 g.

Evaporation, Boiling and Kinetic Theory
- On heating particles gain kinetic energy and move faster.
- In evaporation and boiling the highest kinetic energy molecules can ‘escape’ from the attractive forces of the other liquid particles.
- The particles lose any order and become completely free to form a gas or vapour.
- Energy is needed to overcome the attractive forces in the liquid and is taken in from the surroundings.
- This means heat is taken in, so evaporation or boiling are endothermic (require energy input) processes.
- If the temperature is high enough boiling takes place. Boiling is rapid evaporation anywhere in the bulk liquid and at a fixed temperature called the boiling point and requires continuous addition of heat.
- The rate of boiling is limited by the rate of heat transfer into the liquid.
- Evaporation takes place more slowly at any temperature between the melting point and boiling point, and only from the surface, and results in the liquid becoming cooler due to loss of higher kinetic energy particles.
Differences Between Evaporation and Boiling
| Evaporation | Boiling |
| Takes place on the surface of the liquid | Takes place throughout the liquid |
| Causes cooling | Does not cause cooling |
| Occurs at any temperature although the rate increases with increasing temperature | Occurs only at the boiling point and no temperature change can occur during boiling |
| Only a few molecules have enough energy to escape | All molecules have the same energy and can escape |
Factors that Affect the Rate of Evaporation
Evaporation occurs at all temperatures at the surface of the liquid. It happens more rapidly when
- The temperature is higher, since then more molecules in the liquid are moving fast enough to escape from the surface,
- The surface area of the liquid is large so giving more molecules a changes to escape because more are near the surface, and
- Wind or draught is blowing over the surface carrying vapour molecules away from the surface thus stopping them from returning to the liquid and making it easier for more liquid molecules to break free.

Kinetic Theory and Gas Laws
- Due to the kinetic theory we begin to understand why gases exert pressure.
- The molecules of a gas are far apart and in continuous random motion, colliding with each other and with the walls of the vessel in which the gas is held.
- The molecules have mass, so they have energy hence they exert force on each collision and hence pressure.
- If the temperature of the gas is increased at constant volume, the molecules gain more energy and move faster, hitting the walls with more force and exerting greater pressure.
- If the volume of the gas is increased at constant temperature, the molecules have more space in which to move. The frequency of collisions decreases reducing the pressure.
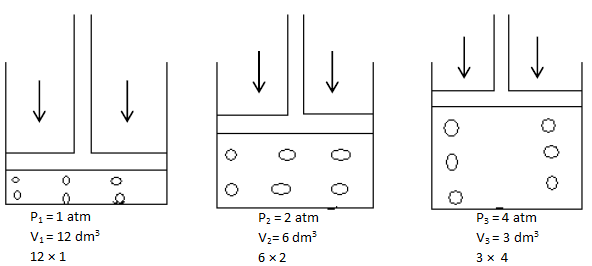
Boyle’s Law
- The pressure of a fixed mass of gas is inversely proportional to its volume if its temperature is kept constant.
- Consider a gas trapped in a container as shown. The mass, hence number of moles are constant and do not change during the course of the investigation. The piston is frictionless and moves smoothly without allowing the gas to escape. When the pressure changes, the volume of the gas changes as shown.
P1V1 = P2V2 = P3V3
∴ PV = constant at constant temperature and mass.
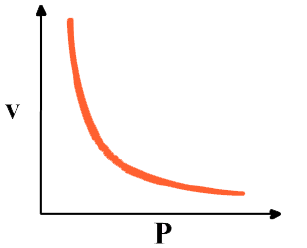
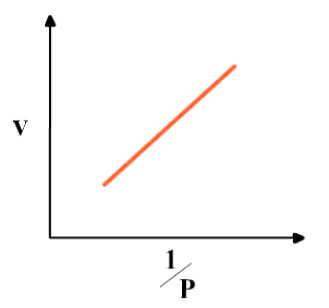
Graphical representation of Boyle’s law
Graph between P & V at constant temperature is a smooth curve known as "parabola"
Graph between 1/P & V at constant temperature is a straight line.
If pressure, p is doubled, the volume is halved. That is, p is inversely proportional to V. In symbols
P ∝ 1/V or p = constant X 1/V
PV = constant
P1V1 = P2V2 = constant. This is Boyle’s law
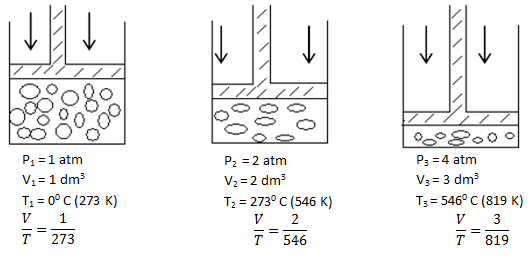
Charles’ Law
- The volume of a fixed mass of gas is directly proportional to its absolute temperature if the pressure is kept constant.
- We can then say that the volume V is directly proportional to the absolute temperature T, i.e. doubling T doubles V, etc. Therefore
V ∝ T or V = constant X T
Or V/T = Constant
Equation V1/T1 = V2/T2 = V3/T3
∴ V/T = constant
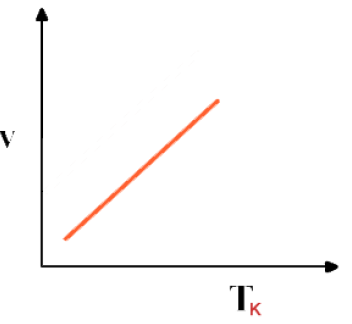
Graphical representation - Graph between Volume and absolute temperature of a gas at constant pressure is a "straight line"
Absolute scale of temperature or absolute zero- If the graph between V and T is extrapolated, it intersects T-axis at -273.16 0C. At -273.16 0C volume of any gas theoretically becomes zero as indicated by the graph.
- But practically volume of a gas can never become zero. Actually no gas can achieve the lowest possible temperature and before -273.16 0C all gases are condensed to liquid. This temperature is referred to as absolute scale or absolute zero.
- At -273.16 0C all molecular motions are ceased. This temperature is called Absolute Zero.
- Degrees on this scale are called Kelvin’s and are denoted by K while θ stands for a Celsius scale temperature. They are exactly the same size as Celsius degrees. Since –273 0C = 0K, conversions from 0C to K are made by adding 273.
T = 273 + θ
00 C = 273K
150 C = 273 + 15 = 288K - The letter T represents Kelvin or absolute temperatures and θ stands for a Celsius scale temperature.
- If the graph between V and T is extrapolated, it intersects T-axis at -273.16 0C. At -273.16 0C volume of any gas theoretically becomes zero as indicated by the graph.
Pressure law
- The pressure of a fixed mass of gas is directly proportional to its absolute temperature if the volume is kept constant.
P ∝ T or P = Constant X T
Or
P= Constant
T - The three equations can be combined giving
PV/T = constant - For cases in which P, V and T all change from say P1, V1 and T1 to P2, V2 and T2, then
P1V1 = P2V2
T1 T2

Gases and the Kinetic Theory
The kinetic theory can explain the behaviour of gases
- Causes of gas pressure
All the molecules in a gas are in rapid motion, with a wide range of speeds, and repeatedly hit the walls of the container in huge numbers per second. The average force and hence the pressure they exert on the walls is constant since pressure is force on unit area. - Boyle’s law
If the volume of a fixed mass of gas is halved by halving the volume of the container, the number of molecules per cm3 will be doubled. There will be twice as many collisions per second with the walls, i.e. the pressure is doubled. This is Boyle’s law. - Temperature
When a gas is heated and its temperature rises, the average speed of its molecules increases. If the volume of the gas is to remain constant, its pressure increases due to more frequent and more violent collisions of the molecules with the walls. If the pressure of the gas is to remain constant, the volume must increase so that the frequency of collisions does not.
Download GAS LAWS - Chemistry Notes Form 3.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students