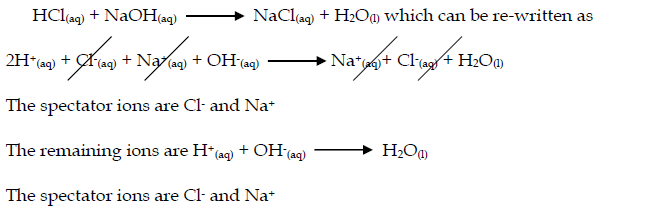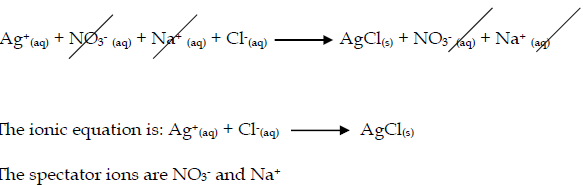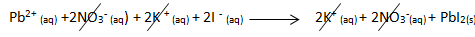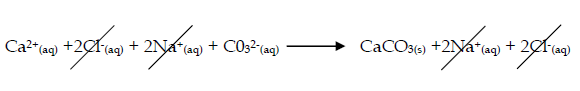Mole Concept
What is a Mole?
- A mole is a word which represents a number. Like the word "dozen" represents the number 12, so "mole" represents the number 6 x 1023.
- This number is also called Avogadro's number.
- It is a very very big number (6 followed by 23 zeros).
- In the same way that you can have a dozen atoms, or cars, or apples, so you can also have a mole of atoms, or cars, or apples.
- Needless to say, chemists are concerned with atoms, ions, molecules and compounds. A mole is defined as the number of atoms in exactly 12 grams of 12C (carbon twelve).
- The number is called Avogadro's number. In the above definition, 12 is the mass number of carbon. So, one mole of carbon atoms has a mass of 12 grams. The relative atomic mass, which can be written as Ar or RAM, is the number just above the element in the periodic table
Relative Atomic Mass(R.A.M) and Moles
- Just as one mole of carbon atoms has a mass of 12 g, so the mass of one mole of the atoms of any element is its "relative atomic mass" in grams.
- For example, look up the relative atomic mass of sodium (Na), (the larger number above it in the periodic table).
- One mole of sodium has a mass of 23 g.
- One mole of helium has a mass of 4 g,
- One mole of neon has a mass of 20 g,
- One mole of magnesium has a mass of 24 g,
- One mole of calcium has a mass of 40 g.
- This is easy for elements which exist as atoms.
- As discussed ealier, the number of protons added to the number of neutrons is known as the relative atomic mass.
- This is the mass of 1 mol of an atom relative to the mass of 1 mol of C atoms that have 6 protons and 6 neutrons, which is taken to be 12.00 g.
- However there are complications due to isotopes and so very accurate atomic masses are not whole numbers.
- Isotopes are atoms of the same element with different masses due to different numbers of neutrons.
- The very accurate atomic mass scale is based on a specific isotope of carbon, carbon - 12, 12C = 12.0000 units exactly, for most purposes C = 12 is used for simplicity.
- The strict definition of relative atomic mass (Ar) is that it is equals average mass of all the isotopic atoms present in the element compared to 1/12th the mass of a carbon-12 atom.
Examples of relative atomic mass calculations
Example 1: Chlorine consists of 75% chlorine-35 and 25% chlorine-37. Calculate its relative atomic mass
Solution: Think of the data based on 100 atoms, so 75 have a mass of 35 and 25 atoms have a mass of 37.
The average mass = [ (75 x 35) + (25 x 37) ] / 100 = 35.5
So the relative atomic mass of chlorine is 35.5 or Ar(Cl) = 35.5
What about elements which exist as molecules or compounds?
Relative Formula Mass of a Compound (R.F.M)
- To calculate the mass of one mole of a compound, the number of each type of atom in the compound is multiplied by that atoms relative atomic mass and all those numbers added together.
- This value is called the relative formula mass (or relative molecular mass or molar mass) of a compound
- NB: Notice that r.f.m, r.m.m, or Mr have no units because they are ratios. The molar mass is obtained from r.f.m, r.m.m, or Mr by simply adding g (grams)
- If all the individual atomic masses of all the atoms in a formula are added together you have calculated the relative formula mass (for ionic compounds) or molecular mass (for covalent elements or compounds).
- Mr. can be used for any element or compound. Whereas relative atomic mass (above) only applies to a single atom.
- Anything with at least two atoms requires the term relative formula/molecular mass.
- The most common error is to use atomic/proton numbers instead of atomic masses, unfortunately, except for hydrogen, they are different!
Examples of formula/molecular mass calculations:
Example 1: Calculate the relative formula mass of the the diatomic molecules of the elements hydrogen H2 and chlorine Cl2. Relative atomic masses, Ar: H = 1, Cl = 35.5
Solution: Formula masses, Mr, are H2 = 2 x 1 = 2, Cl2 = 2 x 35.5 = 71 respectively.
Example 2: Calculate the relative formula mass of the compound calcium hydroxide Ca (OH)2 (ionic). Relative atomic masses are Ca=40, H=1 and O=16
Solution: Mr = 40 + 2 x (16+1) = 74
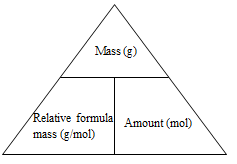
Mass from amount:
- The key mathematical equation needed here is:
Mass (g) = relative formula mass (g mol-1) x amount (mol) - Using the triangular relationship from above if the mass section is covered over then the amount multiplied by the relative formula mass gives the mass.
Examples- What is the mass of 0.25 mol of NaCl?
Solution: 0.25 mol of NaCl = 58.5 g mol-1 × 0.25 mol
= 14.63 g - What is the mass of 3 mol of Al2(SO4)3?
Solution: 3 mol of Al2(SO4)3 = 342 g mol-1 × 3 mol
= 1026 g or 1.026 kg
- What is the mass of 0.25 mol of NaCl?
Amount from Mass
- The key mathematical equation needed here is
Amount (mol) = mass (g)/relative formula mass (g mol-1) - Using the triangular relationship from above if the amount section is covered over then the mass divided by the relative formula mass gives the amount -
Example calculations- What amount is 117 g of NaCl?
Solution: 117 g of NaCl
= 117 g/58.5 g mol-1
= 2 mol - What amount is 68.4 g of Al2(SO4)3?
Solution: 68.4 g of Al2(SO4)3
= 68.4 g/342 g mol-1
= 0.2 mol
- What amount is 117 g of NaCl?
Molar Mass from Mass and Amount
- The key mathematical equation needed here is
Relative formula mass (g mol-1) = mass (g)/amount (mol) - Using the triangular relationship from above if the molar mass section is covered over then the mass divided by the amount gives the relative formula mass.
Example calculations
What is the molar mass of a compound for which 0.2 mol of it has a mass of 42 g?
Solution: molar mass of compound= 42 g/0.2 mol
= 210 g mol-1 - Every mole of any substance contains the same number of the defined species.
- The actual particle number is known and is called the Avogadro Constant and is equal to 6.023 x 1023 'defined species' per mole.
- This means there are that many atoms in 12g of carbon (C = 12) or that many molecules of water in 18g (H2O = 1+1+16 = 18, H = 1; O = 16)
- Note. Relative is just a number based on the carbon-12 relative atomic mass scale.
- Molar mass is a term used to describe the mass of one mole i.e. the relative atomic/formula/molecular mass in grams (g).
Examples:
Example 1: 1 mole of ammonia, NH3, Consists of 1 mole of nitrogen atoms combined with 3 moles of hydrogen atoms. Or you could say 2 moles of ammonia is formed from 1 mole of nitrogen molecules (N2) and 3 moles of hydrogen molecules (H2).
Example 2: 1 mole of aluminium oxide,
Al2O3, consists of 2 moles of aluminium atoms combined with 3 moles of oxygen atoms (or 1.5 moles of O2 molecules). - For calculation purposes learn the following formula for 'Z' and use a triangle if necessary.
- mole of Z = g of Z/atomic or formula mass of Z,
- or g of Z = mole of Z x atomic or formula mass of Z
- or atomic or formula mass of Z = g of Z/mole of Z
where Z represents atoms, molecules or formula of the particular element or compound defined in the question.
Example 1: How many moles of potassium ions and bromide ions in 0.25 moles of potassium bromide?
Solution: 1 mole of KBr contains 1 mole of potassium ions (K+) and 1 mole of bromide ions (Br-). So there will be 0.25 moles of each ion.
Example 2: How many moles of calcium ions and chloride ions in 2.5 moles of calcium chloride?
Solution: 1 mole of CaCl2 consists of 1 mole of calcium ions (Ca2+) and 2 moles of chloride ion (Cl-). So there will be 2.5 x 1 = 2.5 moles of calcium ions and 2.5 x 2 = 5 moles chloride ions.
- Using the Avogadro Constant, you can actually calculate the number of particles in known quantity of material.
Example 3: How many water molecules are there in 1g of water, H2O?
Solution: Formula mass of water = (2 x 1) + 16 = 18
Every mole of a substance contains 6 x 1023 particles of 'it' (the Avogadro Constant).
Moles water = 1/18 = 0.0556
Molecules of water = 0.0556 x 6 x 1023 = 3.34 x 1022
Percentage Composition in a Compound:
- Calculating % Composition (from masses of each element)
Divide the mass of each element by the total mass of the compound and multiply by 100 - Calculating % Composition (from formula)
Calculate formula mass
Divide the total atomic mass of each element by the formula mass and multiply by 100
Example 1. What is the percentage of oxygen in carbon dioxide gas?
Solution: mass of oxygen in one mole of carbon dioxide gas = 2×16 g = 32 g
mass of one mole of carbon dioxide = 12 g + (2×16 g) = 44 g
percentage of oxygen = (32 g/44 g) × 100 = 72.7 %
Example 2. What is the percentage of water of crystallization in hydrated copper (II) sulphate, CuSO4·5H2O?
Solution: mass of water present in one mole of hydrated copper(II) sulphate =(5×18 g) = 90 g
mass of one mole of hydrated copper(II) sulphate = 64 g + 32 g + (4×16 g) + (5×18 g) = 250 g
percentage of water of crystallization present = (90 g/250 g) × 100 = 36 %
Empirical formula of a compound
- This technique covers essentially the reverse of the above process.
- A typical question here involves the calculation of the lowest possible whole number ratio of atoms in an organic molecule, given the percentage elemental composition for that molecule.
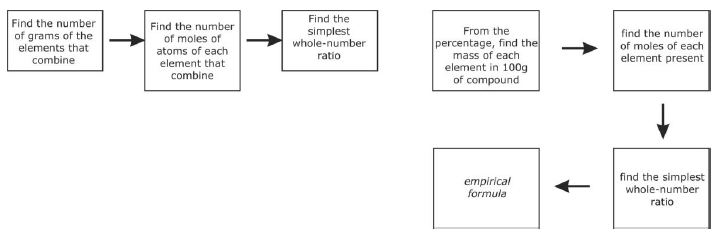
Calculating Empirical Formula (from % Composition) - convert % of each element to grams based on 100 grams of the compound
- multiply grams of each element by 1/molar mass that element
- compare ratio of moles of each element and divide each by the smallest
- if result in step 3 gives a ratio with decimal equivalent to 1/4, 1/3, 1/2, 2.3, 3/4 instead of whole numbers, convert to the fraction and multiply all ratios by the denominator or the fraction
Calculating Empirical Formula (from experimentally determined masses) - multiply the mass of each element (in grams) by 1/molar mass of that element
- Continue with steps 3 & 4 from above.
Example. An organic compound contains carbon and hydrogen only in the ratio of 85.7 % carbon to 14.3 % hydrogen. What is the empirical formula for that compound?
The empirical formula for the compound is CH2.
Molecular formula of a compound
- The molecular formula for a compound is simply the empirical formulae multiplied by some whole number (1, 2, 3, etc...).
- Knowing the molar mass of the compound enables the molecular formula of it to be found.
Finding Molecular Formulas (when molar mass is known) - calculate the empirical formula
- use the equation : (empirical formula mass)x n = molar mass
- find value for n: n = molar mass/empirical formula mass
- multiply each subscript in empirical formula by value for n
Example1. The actual molar mass of the compound in the previous example is 42 g mol-1. What is the molecular formula for this compound?
Solution: The molar mass of CH2 = (12+(2×1)) g mol-1= 14 g mol-1
The molecular formula of this compound is (CH2)n, where n is a positive whole number.
The value of n = 42 g mol-1 / 14 g mol-1 = 3
The molecular formula is (CH2)3 or more properly C3H6.
Examples of where the empirical formula is the same as the molecular formula
Water H2O, methane CH4, propane C3H8 (these molecular formula cannot be 'simplified')
Examples of where the molecular formula is different from the empirical formula
Ethane C2H6 (CH3), phosphorus (V) oxide P4O10 (P2O5), benzene C6H6 (CH)
Three examples are set out below to illustrate all the situations. The relative atomic masses of the elements (Ar) are given in the tabular format method of solving the problem.
Example 2: 1.35g of aluminium was heated in oxygen until there was no further gain in weight. The white oxide ash formed weighed 2.55g. Deduce the empirical formula of aluminium oxide. Note: to get the mass of oxygen reacting, all you have to do is to subtract the mass of metal from the mass of the oxide formed.
Ratios Aluminium, Al (Ar =27) Oxygen, O (Ar = 16) Comments and tips Reacting mass 1.35 g 2.55 − 1.35 = 1.2 g not the real atom ratio moles (mass in g/Ar) 1.35/27 = 0.05 mol 1.2/16 = 0.075 mol can now divide by smallest ratio number or scale up by x factor to get simplest whole number ratio Simplest whole number ratios by trial and error 0.05/0.05 = 1 (then x 2 = 2) or 0.05 x 40 = 2 0.075/0.05 = 1.5 (then x 2 = 3) or 0.075 x 40 = 3 therefore the simplest ratio = empirical therefore the formula for aluminium oxide = Al2O3
Example 3: A chlorinated hydrocarbon compound when analysed, consisted of 24.24% carbon, 4.04% hydrogen, 71.72% chlorine. The molecular mass was found to be 99 from another experiment. Deduce the empirical and molecular formula. (you can 'treat' the %'s as if they were grams, and it all works out like examples 1 and 2)
Ratios Carbon, (Ar =12) Hydrogen, (Ar = 1) Chlorine (Ar = 35.5) Comments and tips Reacting mass or % mass 24.24 g 4.04 g 71.72 just think of it as based on 100g moles (mass in g/Ar) 24.24/12 = 2.02 mol 4.04/1 = 4.04 mol 71.72/35.5 = 2.02 mol can now divide by smallest ratio number Simplest whole number ratios by trial and error 2.02/2.02 = 1 4.04/2.02 = 2 2.02/2.02 = 1 therefore the simplest ratio = empirical formula for the chlorinated hydrocarbon = CH2Cl BUT the molecular mass is 99, and the empirical formula mass is 49.5 (12+2+35.5) AND 99/49.5 = 2, and so the molecular formula must be 2 x CH2Cl = C2H4Cl2
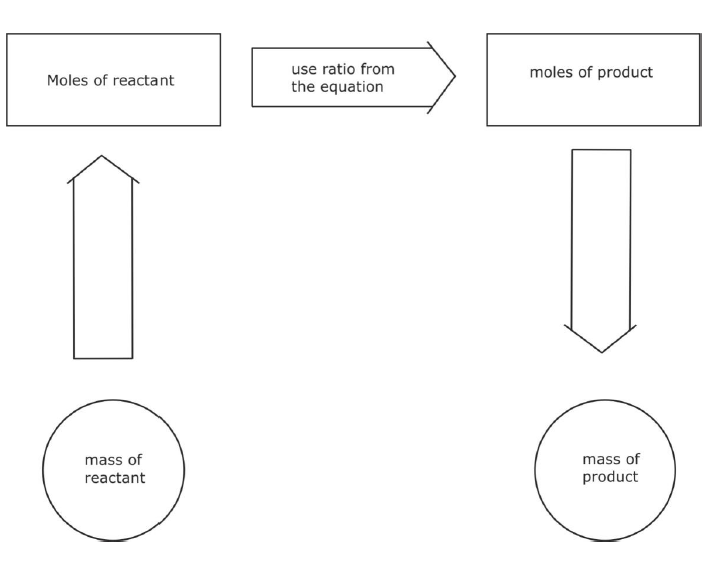
Reacting Mass Calculations
- You can use the ideas of relative atomic, molecular or formula mass and the law of conservation of mass to do quantitative calculations in chemistry.
- Underneath an equation you can add the appropriate atomic or formula masses.
- This enables you to see what mass of what, reacts with what mass of other reactants.
- It also allows you to predict what mass of products are formed (or to predict what is needed to make so much of a particular product).
- You must take into account the balancing numbers in the equation (e.g. 2Mg), as well of course, the numbers in the formula (e.g. O2).
- NOTE: The symbol equation must be correctly balanced to get the right answer!
Example 1:- In a copper smelter, how many tonne of carbon (charcoal, coke) is needed to make 16 tonne of copper?
Solution: 2CuO(s) + C(s)→ 2Cu(s) + CO2(g) (atomic masses Cu=64, O=16, C=12)Formula Mass ratio is 2 x (64+16) + (12) → 2 x (64) + (12 + 2x16)
= Reacting mass ratio 160 + 12 → 128 + 44
(In the calculation, impurities are ignored)
12 of C makes 128 of Cu
Scaling down numerically: mass of carbon needed
= 12 x 16/128 = 1.5 tonne of C - How many tones of copper can be made from 640 tones of copper oxide ore?
Solution: 160 of CuO make 128 of Cu (or direct from formula 80 CuO → 64 Cu)
Scaling up numerically: mass copper formed
= 128 x 640/160 = 512 tones
Example 2:
What mass of carbon is required to reduce 20 tonne of iron(II) oxide ore if carbon monoxide is formed in the process as well as iron? (Atomic masses: Fe = 56, O = 16)
Solution: Reaction equation: Fe2O3 + 3C → 2Fe + 3CO
Formula mass Fe2O3 = (2x56) + (3x16) = 160
160 mass units of iron oxide reacts with 3 x 12 = 36 mass units of carbon
So the reacting mass ratio is 160: 36
So the ratio to solve is 20: x, scaling down,
x = 36 x 20/160 = 4.5 tones carbon needed.
Note: Fe2O3 + 3CO → 2Fe + 3CO2 is the other most likely reaction that reduces the iron ore to iron.
- In a copper smelter, how many tonne of carbon (charcoal, coke) is needed to make 16 tonne of copper?
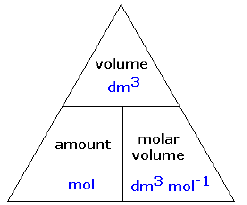
Molar Volume of Gas
- Avogadro's Law states that equal volumes of gases under the same conditions of temperature and pressure contain the same number of molecules.
- So the volumes have equal moles of separate particles in them. One mole of any gas (or the formula mass in g), at the same temperature and pressure occupies the same volume.
- This is 24dm3 (24 litres) or 24000 cm3, at room temperature and pressure (r.t.p.).
Avogadro’s Law and Molar Volume - Equal volumes of all gases contain the same number of molecules. In this table, N =6.02 X 1023 molecules, while V= 24000 cm3 at room temperature and pressure (r.t.p), or 22400 cm3 at standard temperature and pressure (s.t.p).
r.t.p = 250C and 1atmosphere pressure
s.t.p = 00C and 1 atmosphere pressure
RMM Molecules SO2 1 mole 64g N V dm3 CO2 1 mole 44g N V dm3 NH3 1 mole 17g N V dm3 H2 1 mole 2g N V dm3 - 1 mole of any gas always contains the same number of molecules (6.02 X 1023) and hence has the same volume (at the same temperature and pressure).
- When gases combine, they do so in small volumes which bear a simple ratio to one another and to the volume of product if gaseous. All volumes must be measured at the same temperature and pressure.
- Some handy relationships for substance Z below:
- moles Z = mass of Z gas (g) / atomic or formula mass of gas Z (g/mol)
- mass of Z in g = moles of Z x atomic or formula mass of Z
- atomic or formula mass of Z = mass of Z / moles of Z
- 1 mole = formula mass of Z in g.
- gas volume of Z = moles of Z x molar volume
- moles of Z = gas volume of Z / molar volume
Example 1: What is the volume of 3.5g of hydrogen? [Ar(H) = 1]
Answer: Hydrogen exists as H2 molecules, so Mr(H2) = 2, so 1 mole or Formula mass in g = 2g
So moles of hydrogen = 3.5/2 = 1.75 mol H2
So volume H2 = mol H2 x molar volume = 1.75 x 24 = 42 dm3 (or 42000 cm3)
Example 2: Given the equation MgCO3(s) + H2SO4(aq) → MgSO4(aq) + H2O(l) +CO2(g)
What mass of magnesium carbonate is needed to make 6 dm3 of carbon dioxide at r.t.p? [Ar's: Mg = 24, C = 12, O = 16, H =1 and S = 32]
Answer;- method (a):
Since 1 mole = 24 dm3, 6 dm3 is equal to 6/24 = 0.25 mol of gas
From the equation, 1 mole of MgCO3 produces 1 mole of CO2, which occupies a volume of 24 dm3.
So 0.25 moles of MgCO3 is need to make 0.25 mol of CO2
Formula mass of MgCO3 = 24 + 12 + 3x16 = 84,
So required mass of MgCO3 = mol x formula mass = 0.25 x 84 = 21g - Method (b):
Converting the equation into the required reacting masses ..
Formula masses: MgCO3 = 84 (from above), CO2 = 12 + 2x16 = 44
MgCO3: CO2 equation ratio is 1 : 1
so 84g of MgCO3 will form 44g of CO2
44g of CO2 will occupy 24dm3
so scaling down, 6 dm3 of CO2 will have a mass of 44 x 8/24 = 11g
if 84g MgCO3 → 44g of CO2, then ...
21g MgCO3 → 11g of CO2 by solving the ratio, scaling down by factor of 4
- method (a):
Reacting Gases
- Avogadro's Law states that 'equal volumes of gases at the same temperature and pressure contain the same number of molecules' or moles of gas.
- This means the molecule ratio of the equation automatically gives us the gas volumes ratio of reactants and products, if all the gas volumes are measured at the same temperature and pressure.
- This calculation only applies to gaseous reactants or products AND if they are all at the same temperature and pressure.
Example 1: HCl(g) + NH3(g) → NH4Cl(s)
Answer: 1 volume of hydrogen chloride will react with 1 volume of ammonia to form solid ammonium chloride
e.g. 25cm3 + 25cm3 → products or 400dm3 + 400 dm3 →products (no gas formed)
Example 2: N2(g) + 3H2(g) → 2NH3(g)
Answer: 1 volume of nitrogen reacts with 3 volumes of hydrogen to produce 2 volumes of ammonia
e.g. 50 cm3 nitrogen reacts with 150 cm3 hydrogen (3 x 50) →100 cm3 of ammonia (2 x 50)
Example 3: C3H8(g) + 5O2(g) CO2(g) + 4H2O(l)- What volume of oxygen is required to burn 25cm3 of propane, C3H8.
- Theoretical reactant volume ratio is C3H8 : O2 is 1 : 5 for burning the fuel propane.
- so actual ratio is 25 : 5x25, so 125cm3 oxygen is needed.
- What volume of carbon dioxide is formed if 5dm3 of propane is burned?
- heoretical reactant-product volume ratio is C3H8 : CO2 is 1 : 3
- so actual ratio is 5 : 3x5, so 15dm3 carbon dioxide is formed.
- What volume of air (1/5th oxygen) is required to burn propane at the rate of 2dm3 per minute in a gas fire?
- Theoretical reactant volume ratio is C3H8 : O2 is 1 : 5
- so actual ratio is 2 : 5x2, so 10dm3 oxygen per minute is needed,
- Therefore, since air is only 1/5th O2, 5 x 10 = 50dm3 of air per minute is required.
- What volume of oxygen is required to burn 25cm3 of propane, C3H8.

Stoichiometric and Ionic Equations
Chemical Word Equations
- For any reaction, what you start with are called the reactants, and what you form are called the products. So any chemical equation shows in some way the overall chemical change of.
REACTANTS → PRODUCTS - This can be written in words or symbols/formulae.
- The arrow → means the direction of change from reactants to products
- No symbols or numbers are used in word equations. Always try to fit all the words neatly lined up from left to right, especially if it is a long word equation.
- The word equation is presented to summarise the change of reactants to products.
Stoichiometric Equations
- Consider the reaction between zinc sulphide and oxygen. The equation can be written as;
ZnS(s) + O2(g) → ZnO(s) + SO2(g) - This is an example of a stoichiometric, or normal chemical (or symbol) equation.
- From this equation, we can deduce;
- What substances react(zinc sulphide (solid) and oxygen(gas)
- What products are formed (zinc oxide(solid) and sulphur dioxide(gas)
- Relative number of atoms and molecules taking part in the chemical reaction
- The state symbols(s), (l) or (g) to tell us the state of each reactant and each product.
Rules on Balancing Symbol equations
- You should know what the reactants and products are,
- write a word equation with appropriate reactants on the left and products on the right.
- Writing the correct symbol or formula for each equation component.Numbers in a formula are written as subscripts after the element concerned
- e.g. H2SO4 means 2 H's, 1 S and 4 O's
- or the subscript number can double, treble etc. a part of the formula
- e.g. Ca(OH)2 means 1 Ca and 2 OH's (or 2 O's and 2 H's in total)
Numbers before a formula double or treble it etc. - e.g. 2NaCl means 2 Na's and 2 Cl's in total
- or 2H2SO4 means 2 x H2SO4 = 4 H's, 2 S's and 8 O's in total
NOTE: If the number is 1 itself, by convention, no number is shown in a formula or before a formula.
- Using numbers if necessary to balance the equation.
- If all is correct, then the sum of atoms for each element should be the same on both side of the equation arrow.
- in other words: atoms of products = atoms of reactants
This is a chemical conservation law of atoms and later it may be described as the 'law of conservation of mass. - the equations are first presented in 'picture' style and then written out fully with state symbols
- The individual formulas involved and the word equations have already been presented above.
- in other words: atoms of products = atoms of reactants
Ionic Equations
- In many reactions only certain ions change their 'chemical state' but other ions remain in exactly the same original physical and chemical state.
- The ions that do not change are called 'spectator ions'.
- The ionic equation represents the 'actual' chemical change and omits the spectator ions.
- Acid-base reactions: Acids can be defined as proton donors. A base can be defined as a proton acceptor. Any acid-alkali neutralisation involves the hydroxide ion is (base) and this accepts a proton from an acid.
- Insoluble salt formation: An insoluble salt is made by mixing two solutions of soluble compounds to form the insoluble compound in a process called 'precipitation'. A precipitation reaction is generally defined as 'the formation of an insoluble solid on mixing two solutions or a gas bubbled into a solution'.
- Silver chloride is made by mixing solutions of solutions of silver nitrate and sodium chloride.
- silver nitrate + sodium chloride → silver chloride + sodium nitrate
- silver nitrate + sodium chloride → silver chloride + sodium nitrate
- Lead (II) iodide can be made by mixing lead (II) nitrate solution with potassium iodide solution.
- Lead (II) nitrate + potassium iodide → lead (II) iodide + potassium nitrate
- Pb(NO3)2(aq) + 2KI(aq) → PbI2(s) + 2KNO3(aq)
- The ionic equation is: Pb2+(aq) + 2I-(aq) PbI2(s)
- The spectator ions are NO3- and K+
- Lead (II) nitrate + potassium iodide → lead (II) iodide + potassium nitrate
- Calcium carbonate forms on e.g. mixing calcium chloride and sodium carbonate solutions
- Calcium chloride + sodium carbonate → calcium carbonate + sodium chloride
CaCl2(aq) + Na2CO3 (aq) → CaCO3(s) + 2NaCl(aq) - Ionically : Ca2+(aq) + CO32-(aq) → CaCO3(s)
- The spectator ions are Cl- and Na+
- Calcium chloride + sodium carbonate → calcium carbonate + sodium chloride
- Silver chloride is made by mixing solutions of solutions of silver nitrate and sodium chloride.
- Redox reaction analysis:
- Magnesium + iron (II) sulphate → magnesium sulphate + iron
- Mg(s) + FeSO4(aq) → MgSO4(aq) + Fe(s)
- This is the 'ordinary molecular' equation for a typical metal displacement reaction, but this does not really show what happens in terms of atoms, ions and electrons, so we use ionic equations like the one shown below.
- The sulphate ion SO42-(aq) is called a spectator ion, because it doesn't change in the reaction and can be omitted from the ionic equation. No electrons show up in the full equations because electrons lost by x = electrons gained by y!!
- Ionic equation is: Mg(s) + Fe2+(aq) → Mg2+(aq) + Fe(s)
Mg oxidised by electron loss, Fe2+ reduced by electron gain.
- Zinc + hydrochloric acid → zinc chloride + hydrogen
- Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g)
- The chloride ion Cl- is the spectator ion
- Ionic Equation is: Zn(s) + 2H+(aq) → Zn2+(aq) + H2(g)
- Zn oxidised by electron loss, H+ reduced by electron gain.
- Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g)
- Magnesium + iron (II) sulphate → magnesium sulphate + iron

Molarity
- It is very useful to be known exactly how much of a dissolved substance is present in a solution of particular concentration or volume of a solution.
- So we need a standard way of comparing the concentrations of solutions.
- The concentration of an aqueous solution is usually expressed in terms of moles of dissolved substance per cubic decimetre, mol dm-3, this is called molarity, sometimes denoted in shorthand as M.
- Note: 1dm3 = 1 litre = 1000ml = 1000 cm3, so dividing cm3/1000 gives dm3, which is handy to know since most volumetric laboratory apparatus is calibrated in cm3 (or ml), but solution concentrations are usually quoted in molarity, that is mol/dm3 (mol/litre).
- Equal volumes of solution of the same molar concentration contain the same number of moles of solute i.e. the same number of particles as given by the chemical formula.
- You need to be able to calculate:
- The number of moles or mass of substance in an aqueous solution of given volume and concentration
- The concentration of an aqueous solution given the amount of substance and volume of water.
- You should recall and be able to use each of the following relationships.
- molarity of Z = moles of Z / volume in dm3
- molarity x formula mass of solute = solute concentration in g/dm3, dividing this by 1000 gives the concentration in g/cm3
- (concentration in g/dm3) / formula mass = molarity in mol/dm3,
- moles Z = mass Z / formula mass of Z
- 1 mole = formula mass in grams
Example 1
What mass of sodium hydroxide (NaOH) is needed to make up 500 cm3 (0.5 dm3) of a 0.5M solution? [Ar's: Na = 23, O = 16, H = 1]
1 mole of NaOH = 23 + 16 + 1 = 40g
for 1000 cm3 (1 dm3) of 0.5M you would need 0.5 moles NaOH
which is 0.5 x 40 = 20ghowever only 500 cm3 of solution is needed compared to 1000 cm3
so scaling down: mass NaOH required = 20 x 500/1000 = 10g
Example 2
How many moles of H2SO4 are there in 250cm3 of a 0.8M sulphuric acid solution? What mass of acid is in this solution? [Ar's: H = 1, S = 32, O = 16]
formula mass of sulphuric acid = 2 + 32 + (4x16) = 98, so 1 mole = 98g
if there was 1000 cm3 of the solution, there would be 0.8 moles H2SO4
but there is only 250cm3 of solution, so scaling down ...
moles H2SO4 = 0.8 x (250/1000) = 0.2 mol
mass = moles x formula mass, which is 0.2 x 98 = 19.6g of H2SO4
Example 3
5.95g of potassium bromide was dissolved in 400cm3 of water. Calculate its molarity. [Ar's: K = 39, Br = 80]
moles = mass / formula mass, (KBr = 39 + 80 = 119)
mol KBr = 5.95/119 = 0.05 mol
400 cm3 = 400/1000 = 0.4 dm3
molarity = moles of solute / volume of solution
molarity of KBr solution = 0.05/0.4 = 0.125M
Example 4
What is the concentration of sodium chloride (NaCl) in g/dm3 and g/cm3 in a 1.50 molar solution?
At. Masses: Na = 23, Cl = 35.5, formula mass NaCl = 23 + 35.5 = 58.5
Therefore concentration = 1.5 x 58.5 = 87.8 g/dm3, and concentration = 87.75 / 1000 = 0.0878 g/cm3
Example 5
A solution of calcium sulphate (CaSO4) contained 0.5g dissolved in 2dm3 of water. Calculate the concentration in (a) g/dm3, (b) g/cm3 and (c) mol/dm3.- concentration = 0.5/2 = 0.25 g/dm3, then since 1dm3 = 1000 cm3
- concentration = 0.25/1000 = 0.00025 g/cm3
- At. masses: Ca = 40, S = 32, O = 64, f. mass CaSO4 = 40 + 32 + (4 x 16) = 136
moles CaSO4 = 0.5 / 136 = 0.00368 mol
concentration CaSO4 = 0.00368 / 2 = 0.00184 mol/dm3

Titration: Acid and Alkali
- Titrations can be used to find the concentration of an acid or alkali from the relative volumes used and the concentration of one of the two reactants.
- You should be able to carry out calculations involving neutralisation reactions in aqueous solution given the balanced equation or from your own practical results.
- Note again: 1dm3 = 1 litre = 1000ml = 1000 cm3, so dividing cm3/1000 gives dm3.
- and other useful formulae or relationships are:
- moles = molarity (mol/dm3) x volume (dm3=cm3/1000),
- molarity (mol/dm3) = mol / volume (dm3=cm3/1000),
- 1 mole = formula mass in grams.
- In most volumetric calculations of this type, you first calculate the known moles of one reactant from a volume and molarity. Then, from the equation, you relate this to the number of moles of the other reactant, and then with the volume of the unknown concentration, you work out its molarity.
Example 1:
25 cm3 of a sodium hydroxide solution was pipetted into a conical flask and titrated with 0.2M hydrochloric acid. Using a suitable indicator it was found that 15 cm3 of acid was required to neutralise the alkali. Calculate the molarity of the sodium hydroxide and concentration in g/dm3.
Equation NaOH(aq) + HCl(aq) → NaCl(aq) + H2O(l)
moles HCl = (15/1000) x 0.2 = 0.003 mol
moles HCl = moles NaOH (1 : 1 in equation)
so there is 0.003 mol NaOH in 25 cm3
scaling up to 1000 cm3 (1 dm3), there are ...
0.003 x (1000/25) = 0.12 mol NaOH in 1 dm3
molarity of NaOH is 0.12M or mol dm-3
since mass = moles x formula mass, and Mr(NaOH) = 23 + 16 + 1 = 40
concentration in g/dm3 is 0.12 x 40 = 4.41g/dm3
Example 2:
20 cm3 of a sulphuric acid solution was titrated with 0.05M potassium hydroxide. If the acid required 36 cm3 of the alkali KOH for neutralisation what was the concentration of the acid?
equation 2KOH(aq) + H2SO4(aq) →K2SO4 + 2H2O(l)
mol KOH = 0.05 x (36/1000) = 0.0018 mol
mol H2SO4 = mol KOH / 2 (because of 1 : 2 ratio in equation above)
mol H2SO4 = 0.0018/2 = 0.0009 (in 20 cm3)
scaling up to 1000 cm3 of solution = 0.0009 x (1000/20) = 0.045 mol
mol H2SO4 in 1 dm3 = 0.045, so molarity of H2SO4 = 0.045M or mol dm-3
since mass = moles x formula mass, and Mr(H2SO4) = 2 + 32 + (4x16) = 98
Concentration in g/dm3 is 0.045 x 98 = 4.41g/dm3
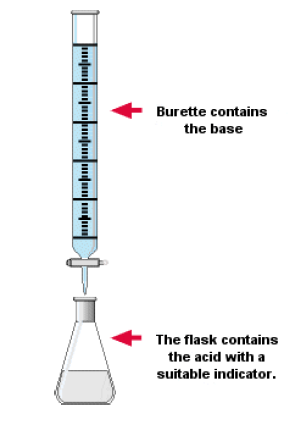
How to carry out a titration
- The diagrams show the typical apparatus (1)-(6) used in manipulating liquids and on the left a brief three stage description of titrating an acid with an alkali:
Volumetric Analysis (Titrations)
- A titration is a laboratory procedure where a measured volume of one solution is added to a known volume of another reagent until the reaction is complete.
- The operation is an example of volumetric (titrimetric) analysis. The equivalence point is usually shown by the colour change of an indicator and is known as the end-point.
- Volumetric analysis is a powerful technique, which is used in a variety of ways by chemists in many different fields.
Practical Aspects
- The practical aspects of titrations are required in the assessment of practical skills
- Knowledge of the techniques of titrations is expected but it would be normal to assume that all apparatus would have been washed with distilled/deionised water. The description should include which reagent is placed in the burette, name of indicator (but no reason for choice of indicator), detection of endpoint and what should be observed, and repetition for accuracy.
When you have finished this section you should be able to
- Perform titrations
- Record titration results in the form of a table
Use of a Volumetric Flask
- To prepare a solution of precisely known concentration (a standard solution), a definite amount of solute must be dissolved in a solvent to give a definite volume of solution.

- The definite amount of material is measured by weighing, and the definite volume of solution prepared in a volumetric flask.
- A volumetric flask contains a definite volume when correctly filled to the calibration mark at the temperature stated on the flask.
- Tip the solid from a weighing bottle into a large (250 cm3) beaker and add about 50 cm3 of distilled water from a wash bottle.
- Stir well with a glass rod to dissolve.
- Take great care not to lose any of the solution and remember to wash the solution off the stirring rod back into the beaker.
- Rinse out the volumetric flask with distilled water and pour the cold solution into the flask through a clean filter funnel.
- Wash out the beaker several times and add all the washings to the flask.
- Now fill the flask to within about 1 cm of the calibration mark on the neck.
- Finally add water dropwise until the meniscus just rests on the calibration mark.
- Stopper the flask and invert a number of times to thoroughly mix the contents.
Use of a Pipette
- The pipette is designed to deliver a definite fixed volume of liquid when correctly filled to its calibration mark.

- Before use, a pipette must be washed out with the solution it is to measure.
- To fill the pipette, use a safety filler to suck solution up a few centimetres above the calibration mark.
- Let the solution down until the bottom of the meniscus just touches the calibration mark.
- For a titration the contents of the pipette are run into a conical flask, which has been well washed with distilled water.
- Allow the pipette to drain for about 20 seconds, then touch the tip to the surface of the liquid in the conical flask.
- The volume of solution delivered by the pipette is known as the aliquot.
Use of a Burette
- The burette is designed to deliver definite but variable volumes of liquid. First rinse out the burette with the solution it is to contain. Clamp the burette vertically in a stand.
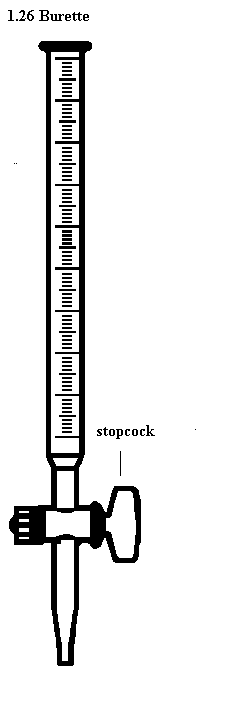
- Fill the burette carefully using a beaker and a filter funnel. Open the tap briefly to fill the burette below the tap making sure there are no trapped air bubbles. Read the burette scale by observing the position of the bottom of the liquid meniscus, making sure your eyes are level with the graduation mark. To observe the meniscus more clearly, hold a white card behind the burette. Record the volume reading to the nearest 0.05 cm3.
Indicator Colour in Acid Neutral color Colour in alkali Litmus Red Purple Blue Phenophthalein Colourless Colourless Pink Methyl orange Red Orange Yellow Universal indicator Red Green Blue/Violet Bromothymol blue Yellow Green Blue
Titration Technique
- When performing a titration, place the conical flask containing the aliquot on a white tile under the burette so that the tip of the burette is inside the mouth of the conical flask to avoid splashing.
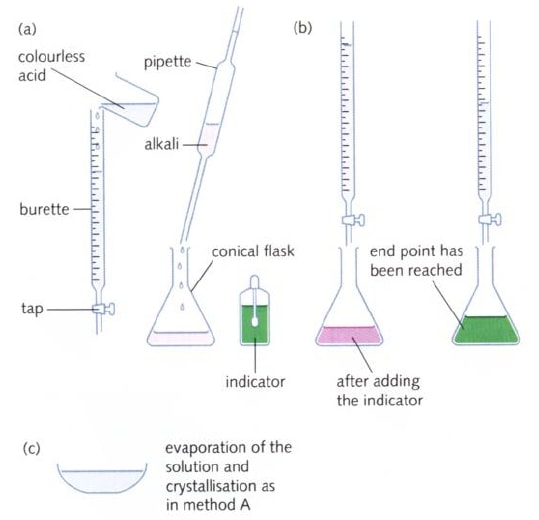
- Add a few drops of a suitable indicator to the solution in the conical flask.
- First perform a ‘rough’ titration by taking the burette reading and running in the solution in approximately 1 cm3 portions, while swirling the flask vigorously.
- When the end-point is reached, as shown by the indicator changing colour, quickly close the tap.
- The new burette reading will give you a rough idea (to within about 1 cm3) of the volume to be added.
- Now repeat the titration with a fresh aliquot. As the rough end-point volume is approached, add solution from the burette one drop at a time until the indicator changes colour.
- Record the volume. The volume run out from the burette to reach the end point is known as the titre.
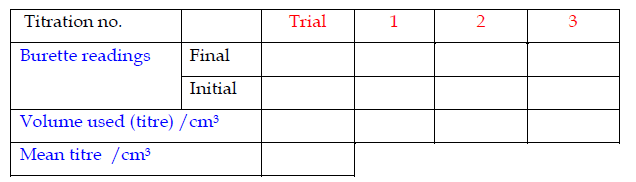
Recording Titration Results
The results of a titration should be recorded;- Immediately
- In ink
- In a table
- To the correct number of decimal places
Record the titrations in form of a table
Accuracy
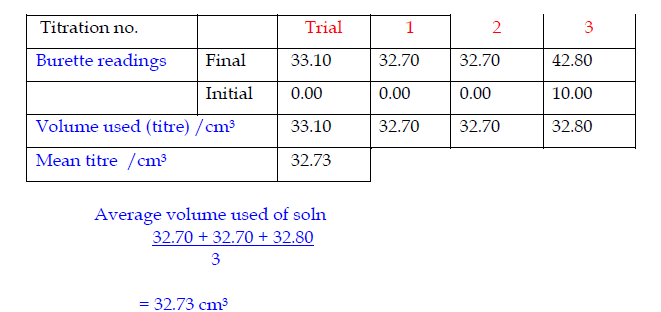
- Record burette readings to the nearest 0.05 cm3 (approximately 1 drop).
- Consecutive titrations should agree to within 0.10 cm3 and, strictly, you should repeat the titrations until this is achieved.
- However you may not have either the time or materials available to do this.
- With practice, your technique should improve so that you should not need to do more than 4 titrations (1 trial + 3 accurate).
- Calculate and use the mean (average) of the two (or preferably three) closest consecutive readings and quote this to the nearest 0.05 cm3.
What do examiners look for in your answer sheet?
CT 1 mark D 1 mark AC 1 mark PA 1 mark FA 1 mark Total 5 marks
Specimen titration Table II
Calculating the Concentration of a Solution from Titration Data
- When you have finished this section you should be able to:
- Calculate the concentration of a solution from titration data and the balanced equation.
- Calculate the volume of solution required for titration from titration data and the balanced equation.
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download THE MOLE: FORMULAE AND CHEMICAL EQUATIONS - Chemistry Notes Form 3.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students