Mathematics Paper 1 - Alliance High School Pre-Trial Examination 2018

121/1
MATHEMATICS
PAPER 1
MAY 2018
TIME: 2¹/₂ HOURS

ALLIANCE HIGH SCHOOL
PRE-TRIAL EXAMINATION 2018

INSTRUCTIONS TO CANDIDATES

• The paper consists of two sections: Section I and II.
• Answer all the questions in section 1 and ONLY 5 in section II.
• Show all the steps in your calculations giving your answers at each stage in the spaces below each question.
• Marks may be given for correct working even if the answer is wrong.
• Non-programmable silect electronic calculator and KNEC examination tables may be used except where stated otherwise.

SECTION 1. ANSWER ALL THE QUESTIONS IN THIS SECTION

1. Evaluate:
   
   
   
   
   
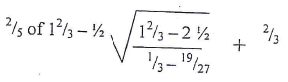
2. Solve for y in the equation
   8(2²)^y = 6(2^y) - 1 (4 mks)
3. A line Ax + 3y - 6 = 0 is perpendicular to the line 5x + 7y - k = 0 passes through the points (4,3). Determing the values of A and K. (4 mks)
4. Two numbers are in the ration 5:7. When 15 is added to each number, the ration changes to 5:6. Find the two numbers. (3 mks)
5. In the figure below, AB is parallel to DE, DE bisects angle BDG, angle DCF = 60^o angle CFG = 110^o 
   
   
   
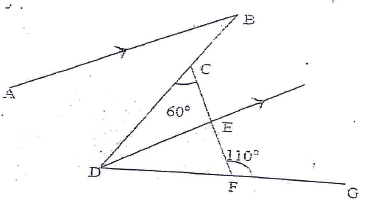
   Find, give reasons for your answers
   
   1. <CDF (2 mks)
   2. <ABD (2 mks)
6. The diagram below shows the sketch of the curve y = x² - x - 6
   
   
   
   
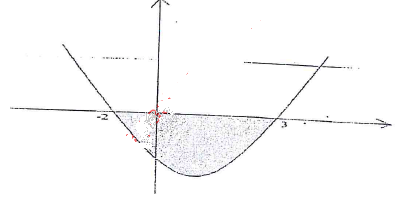
   Using the trapezoidal rule with four trapezia, calculate the area of the shaded region. (4 mks)
7. Simplify the expression completely. (3 mks)
   
   
   
   
   
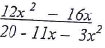
8. Solve the following inequalities, illustrating the solution on a graph.
   
   2x - 1 ≤ 7x + 12 < 5x + 17 (3 mks)
9. Two boys and a girl shared some money. The younger boy got ⁵/₁₈ of it; the elder boy got ⁷/₁₂ of the remainder and the girl got the rest. Find the percentage share of the younger boy to the girl's share. (3 mks)
10. A bus starts off from Kitale at 9am and travels towards Kakamega at a speed of 60km/hr. At 9.50am, a matatu leaves Kakamega and travels towards Kitale at a speed of 60km/h. How far from Kitale will the two vehicles meet. (3 mks)
11. The purchase price of a TV consists of sh 4600 deposit and 8 equal monthly installments of sh 840. Given that the carrying charge is sh 2800, find the cash price. (3 mks)
12. Solve the simultaneous equation: (3 mks)
    Log(x-1) + 2 log y = 2log3
    logx +logy = log6
13. Pieces of soap are packed in a cuboid container measuring 36cm by 24cm by 18cm. Each piece of soap is similar to the container. If the linear scale factor between the container and the soap is ¹/₆, find the volume of each piece of soap and hence determine the number of pieces packed in the container. (4 mks)
14. Two types of coffee cost sh 250 per kg and sh200 per kg are mixed so that their masses are in the ration 3:5 respectively. Otieno sold the mixture at sh 262.50. Calculate his percentage profit. (3 mks)
15. A translation T maps P(5,3) onto P'(2, -5). Find the length of P'R' if point R' is the image of R(-2,-3) under the same translation T. (3 mks)
    
16. Given that Sin(x + 4^o) = Cos(3x)^o . Find tan (x + 40^o) to 4 s.f. (3 mks)

SECTION II. ANSWER ONLY FIVE QUESTIONS FROM THIS SECTION (50 MARKS)

17. Kamene is a sales executive earning a salary of Ksh. 25,000 and a commission of 8% for the sales in excess of Ksh. 100,000
    If in February she earned a total of Ksh. 52,000 in salaries and commission.
    1. Determine the amount of sales she made in that month. (4 mks)
    2. If the total sales in the month of March and April increased by 18% and then dropped by 30% respectively, calculate.
       1. Kamene's commission in the month of March. (3 mks)
       2. Her total earnings in the month of April. (3 mks)
18. Two cylindrical container are similar. The larger one has internal cross-sectional area of 45cm² and can hold 0.945 litres of liquid when full. The smaller containter has internal cross-section area of 20cm².
    1. Calculate the capacity of the smaller container. (4 mks)
    2. The larger container is filled with juice to a height of 13cm. Juice is then drawn from it and emptied into the smaller container until the depths of the juice in both containers are equal. Calculate the depth of the juice in each container. (2 mks)
    3. One fifth of the juice in the larger container in part (b) above is further drawn and emptied into the smaller container. Find the difference in the depths of the juice in the two containers. (4 mks)
19. The table below shows patients who attend a clinic in one week and were grouped by age as shown in the table below.
    
    

    Age x years	0≤x≤5	5≤x≤15	15≤x≤25	25≤x≤45	45≤x≤75
    Number of patients	14	41	59	70	15

    
    
    
    1. Estimate the mean age. (4 mks)
    2. On the grid provided, draw a histogram to represent the distribution. (3 mks)
       Use the scales: 1 cm to represent 5 units on the horizontal axis 2 cm to represent 5 units on the vertical axis.
    3. 1. State the group in which the median mark lies. (1 mk)
       2. A vertical line drawn through the median mark divides the total area of the histogram into two equal. Using this information, estimate the median mark. (2 mks)
20. A cold water tap can fill a bath in 3 minutes, while a hot tap can fill it in 5 minutes. The drain pipe can empty the bath in 3^3/₄ minutes. The two taps and the drain pipe are fully opened for 2 minutes after which the drain pipe is closed.
    1. What fraction of the bath is filled after the first two minutes. (3 mks)
    2. How many seconds are required for the bath to be completely filled? (3 mks)
    3. Given that the cold water tap deliveres water at the rate of 200cm³/s
       Determine
       1. The capacity of the bath in litres. (2 mks)
       2. The rate of flow of the hot water tap (2 mks)
21. Four towns A, B, C and D are such that B is on a bearing of 247^o and 6km from A. C is due SSE and 4.8km from B, D is to the south of A and the bearing of C from D is S44^oW.
    1. Make a scale drawing showing the relative positions of A, B, C and D using the scale 1 cm represents 1km. (4 mks)
    2. Use your drawing to determing
       1. The bearing of A from C. (1 mk)
       2. The distance between C and D. (1 mk)
       3. How far D is east of B. (1 mk)
    3. The average speed of a cyclist from C to A if he takes 30 minutes between A and D and 20 minutes between D and A. (3 mks)
22. 1. Complete the table below for the function y = 6 + x - x²  (2 mks)
       
       

       x	-4	-3	-2	-1	0	1	2	3	4	5
       y	-14				6		4		-6

    2. On the grid provided below, draw the graph of y = 6 - x - x² for -4 ≤ x ≤ 5 (3 mks)
    3. On the same axes, draw the graph of y = 2 - 2x (2 mks)
    4. From the graphs, find the values of x which satisfy the simultaneous equations. (1 mks)
       y = 6 + x - x² 
       y = 2 - 2x
    5. Write down and simplify a quadratic equation in the form ax² + bx + c = 0 which is satisfied by the values of x where the two graphs intersect. (2 mks)
23. The distance S metres from a fixed point, covered by a particle after t seconds is given by the equation:
    S = t³ - 6t² + 9t + 5
    1. Calculate the time when the gradient of the curve is equal to 3.75m (3 mks)
    2. Determine the values of S at the turning points of the curve. (4 mks)
    3. On the space provided, sketch the curve of S = t³ - 6t² + 9t + 5 (3 mks)