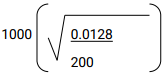- Introduction
- Place Value Chart
- Decimal to Fractions
- Converting a Decimal to a Fraction
- Recurring Decimals
- Decimal Places
- Standard Form
- Operation on Decimals
- Past KCSE Questions on the Topic

Introduction
- A fraction whose denominator can be written as the power of 1 0 is called a decimal fraction or a decimal. E.g.
1/10, 1/100, 50/1000. - A decimal is always written as follows 1/10 is written as 0.1 while 5/100 is written as 0.05.The dot is called the decimal point.
- Numbers after the decimal points are read as single digits e.g. 5.875 is read as five point eight seven five. A decimal fraction such 8.3 means 8 + 3/10.A decimal fraction which represents the sum of a whole number and a proper fraction is called a mixed fraction.

Place Value Chart
| Ten thousands |
Thousands | Hundreds | Tens | Ones | Decimal Point |
Tenths | Hundredths | Thousandths | Ten Thousandths |
Hundred |
| 1 0,000 | 1 ,000 | 1 00 | 1 0 | 1 | . | .1 | .01 | .001 | .0001 | .00001 |

Decimal to Fractions
- To convert a number from fraction form to decimal form, simply divide the numerator (the top number) by the denominator (the bottom number) of the fraction.
Example:
5/8


Converting a Decimal to a Fraction
- To change a decimal to a fraction, determine the place value of the last number in the decimal. This becomesnthe denominator. The decimal number becomes the numerator. Then reduce your answer.
Example:
.625 - the 5 is in the thousandths column, therefore,
.625 = 625/1000 = reduces to 5/8
Note:
- Your denominator will have the same number of zeros as there are decimal digits in the decimal number you started with - .625 has three decimal digits so the denominator will have three zero.

Recurring Decimals
- These are decimal fractions in which a digit or a group of digits repeat continuously without ending.
1/3 = 0.333333
5/11 = 0.454545454 - We cannot write all the numbers, we therefore place a dot above a digit that is recurring. If more than one digit recurs in a pattern, we place a dot above the first and the last digit in the pattern.
E.g. .
0.3333……………………….is written as 0.3
. .
0.4545………………………is written as 0.45
. . .
0.324324………………….is written as 0.324 - Any division whose divisor has prime factors other than 2 or 5 forms a recurring decimal or non-terminating decimal.
Example
Express each as a fraction
.
(a) 0.6
. .
(b) 0.7̇3
. .
(c) 0. ̇15
Solution
- Let r = 0.66666 ------- ( i )
10r = 6.6666 --------------- (ii)
Subtracting i from ii
9r = 6
r = 6/9
= 2/3 - Let r = 0.73333--------- (i)
10r = 7.3333333--------- (ii)
100r = 73.33333--------- (iii)
Subtracting (ii) from (iii)
90r = 66
r = 66/90
=11/15 - Let r = 0.151515 ---------(i)
100r = 15.1515 ----------- (ii)
99r= 15
r =15/99
=5/33

Decimal Places
- When the process of carrying out division goes over and over again without ending we may round off the digits to any number of required digits to the right of decimal points which are called decimal places.
Example
Round 2.832 to the nearest hundredth.
Solution
Step 1 – Determine the place to which the number is to be rounded is.
2.832
Step 2 – If the digit to the right of the number to be rounded is less than 5, replace it and all the digits to the right of it by zeros. If the digit to the right of the underlined number is 5 or higher, increase the underlined number by 1 and replace all numbers to the right by zeros. If the zeros are decimal digits, you may eliminate them.
2.832 = 2.830 = 2.83
Example
Round 43.5648 to the nearest thousandth.
Solution
43.5648 = 43.5650 = 43.565
Example
Round 5,897,000 to the nearest hundred thousand.
Solution
5,897,000 = 5,900,000

Standard Form
- A number is said to be in standard form if it is expressed in form A X 10n, Where 1 < A <1 0 and n is an integer.
Example
Write the following numbers in standard form.
- 36
- 576
- 0.052
Solution
- 36/10 x 10 = 3.6 x 101
- 576/100 x 100 = 5.76 x 102
- 0.052 = 0.052 x 100/100
5.2× 1/100
5.2×(1/100)2
5.2× 10−2

Operation on Decimals
Addition and Subtraction
The key point with addition and subtraction is to line up the decimal points!
Example
2.64 + 11.2
Solution
2.64
+ 11.20 →in this case, it helps to write 11 .2 as 11 .20
13.84
Example
14.73 – 12.155
Solution
14.730 →again adding this 0 helps
−12.155
2.575
Example
127.5 + 0.127
Solution
127.500
+ 0.127
327.627
Multiplication
- When multiplying decimals, do the sum as if the decimal points were not there, and then calculate how many numbers were to the right of the decimal point in both the original numbers - next, place the decimal point in your answer so that there are this number of digits to the right of your decimal point?
Example
2.1 x 1.2
Calculate 21 x 12 = 252.
There is one number to the right of the decimal in each of the original numbers, making a total of two.
We therefore place our decimal so that there are two digits to the right of the decimal point in our answer.
Hence 2.1 x 1.2 =2.52.
Always look at your answer to see if it is sensible. 2 x 1 = 2, so our answer should be close to 2 rather than 20 or 0.2 which could be the answers obtained by putting the decimal in the wrong place.
Example
1.4 x 6
Calculate 14 x 6 = 84.
There is one digit to the right of the decimal in our original numbers so our answer is 8.4
Check 1 x 6 = 6 so our answer should be closer to 6 than 60 or 0.6
Division
- When dividing decimals, the first step is to write your numbers as a fraction. Note that the symbol / is used to denote division in these notes.
Hence 2.14/1.2
= 2.14
1.2 - Next, move the decimal point to the right until both numbers are no longer decimals. Do this the same number of places on the top and bottom, putting in zeros as required.
Hence 2.14/1.2 becomes 214/120 - This can then be calculated as a normal division.
- Always check your answer from the original to make sure that things haven’t gone wrong along the way. You would expect 2.14/1.2 to be somewhere between 1 and 2. In fact, the answer is 1.78.
- If this method seems strange, try using a calculator to calculate 2.14/1.2, 21.4/12, 214/120 and 2140 /1200. The answer should always be the same.
Example
4.36/0.14
4.36 = 436 = 31.14
1.4 14
Example
27.93/1.2
27.93 = 2793 = 23.28
1.2 120
Rounding Up
- Some decimal numbers go on forever! To simplify their use, we decide on a cutoff point and “round” them up or down.
- If we want to round 2.73421 6 to two decimal places, we look at the number in the third place after the decimal, in this case, 4. If the number is 0, 1 , 2, 3 or 4, we leave the last figure before the cut off as it is. If the number is 5, 6, 7, 8 or 9 we “round up” the last figure before the cut off by one. 2.73421 6 therefore becomes 2.73 when rounded to 2 decimal places.
- If we are rounding to 2 decimal places, we leave 2 numbers to the right of the decimal.
- If we are rounding to 2 significant figures, we leave two numbers, whether they are decimals or not.
Example
- 243.7684 = 243.77 (2 decimal places)
= 240 (2 significant figures) - 1973.285 = 1973.29 (2 decimal places)
= 2000 (2 significant figures) - 2.4689 = 2.47 (2 decimal places)
= 2.5 (2 significant figures) - 0.99879 = 1 .00 (2 decimal places)
= 1 .0 (2 significant figures)
Order of Operation
- The same rules on operations is always the same even for decimals.
Examples
Evaluate
0.02 + 3.5 x 2.6 – 0.1 (6.2 − 3.4)
Solution
0.02 + 3.5 x 2.6 – 0.1 x 2.8 = 0.02 + 0.91 − 0.28
= 8.84

Past KCSE Questions on the Topic
- Without using logarithm tables or a calculator evaluate.
384.16 x 0.0625
96.04 - Evaluate without using mathematical table
- Express the numbers 1 470 and 7056, each as a product of its prime factors.
Hence evaluate:
14702
7056
Leaving the answer in prime factor form - Without using mathematical tables or calculators, evaluate
- Evaluate without using mathematical tables or the calculator
0.0625x 2.56
0.25 x 0.08
Download Decimals - Mathematics Form 1 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students