Area - Mathematics Form 1 Notes

• Introduction
  • Units of Areas
• Area of a Regular Plane Figures
  • Areas of a Rectangle
  • Area of a Triangle
  • Area of a Parallelogram
  • Area of a Trapezium
  • Area of a Circle
• Surface Area of Solids
  • Cylinder
• Area of Irregular Shapes
• Past KCSE Questions on the Topic

Introduction

Units of Areas

• The area of a plane shape is the amount of the surface enclosed within its boundaries. It is normally measured in square units. For example, a square of sides 5 cm has an area of
  5 x 5 = 25 cm
• A square of sides 1 m has an area of 1 m, while a square of side 1 km has an area of 1 km

Conversion of Units of Area

1 m² =1 mx 1 m
= 100 cm x 1 00 cm
= 10 000 cm²

1 km² = 1 km x 1 km
= 1 000m x 1 000 m
=1 000 000 m²

1 are = 10 m x 10 m
=100m²

1 hectare (ha) = 100 Ares
=10000 m²

Area of a Regular Plane Figures

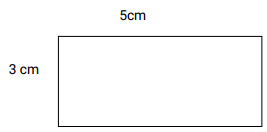
Areas of a Rectangle

Area, A = 5 x 3 cm
=15m²
Hence, the area of the rectangle, A =L X W square units, where l is the length and b breadth.

Area of a Triangle

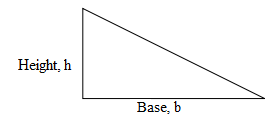
Area of a triangle

A =¹/₂bh square units

Area of a Parallelogram

Area = ¹/₂bh +¹/₂bh
=bh square units

Note:

• This formulae is also used for a rhombus

Area of a Trapezium

The figure below shows a trapezium in which the parallel sides are a units and b units, long. The perpendicular distance between the two parallel sides is h units.

Area of a triangle ABD =¹/₂ ah square units
Area of triangle DBC = ½ bh square units
Therefore area of trapezium ABCD =¹/₂ ah +¹/₂ bh
= ¹/₂h (a + b) square units.
Thus, the area of a trapezium is given by a half the sum of the length of parallel sides multiplied by the perpendicular distance between them.

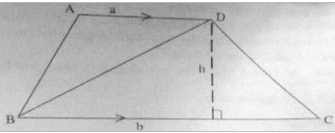
That is, area of trapezium =¹/₂ (a+b)h

Area of a Circle

The area A of a circle of radius r is given by: A = πr²

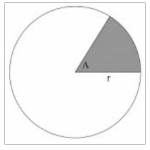
The Area of a Sector

• A sector is a region bounded by two radii and an arc.

Suppose we want to find the area of the shaded part in the figure below

The area of the whole circle is πr²

The whole circle subtends 360ͦ at the centre.

Therefore, 360^o corresponds to πr²
1 ͦ corresponds to ¹/₃₆₀ ͦ x πr²
60 ͦ corresponds to ^{60 ͦ} /₃₆₀ ͦ x πr²
Hence, the area of a sector subtending an angle θ at the centre of the circle is given by
A =  θ   x πr²
    360⁰

Example

Find the area of the sector of a circle of radius 3 cm if the angle subtended at the centre is 140 ͦ (take π=²²/₇)

Solution

Area A of a sector is given by
A = ^θ/₃₆₀ x πr²
Here, r = 3 cm and θ =140⁰
Therefore, A= ¹⁴⁰/_360⁰ x ²²/₇ x 3 x 3
= 11 cm²

Example

The area of a sector of a circle is 38.5 cm². Find the radius of the circle if the angle subtended at the centre is 90⁰ (Take π = ²²/₇)

Solution

From the formula a = θ/360 x πr², we get ⁹⁰/₃₆₀ x ²²/₇ x r² = 38.5
Therefore, r² = 38.5 x 360 x 7
                            90 x 22
Thus, r = 7

Example

The area of a circle radius 63 cm is 41 58 cm². Calculate the angle subtended at the centre of the circle. (Take π=²²/₇)

Solution

Using a =^θ/₃₆₀ x πr²,
θ= 4158 x 7 x 360
      22 x 63 x 63
= 120⁰

Surface Area of Solids

• Consider a cuboid ABCDEFGH shown in the figure below. If the cuboid is cut through a plane parallel to the ends, the cut surface has the same shape and size as the end faces. PQRS is a plane. The plane is called the cross-section of the cuboid
  
  
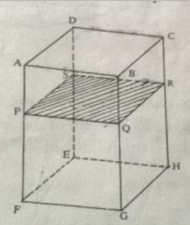
• A solid with uniform cross-section is called a prism. The following are some of the prisms. The following are some of the prisms.
  
  
• The surface area of a prism is given by the sum of the area of the surfaces.
  
  
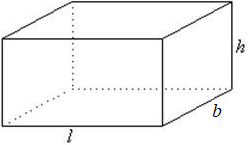
• The figure below shows a cuboid of length l, breath b and height h. its area is given by;
  A=2lb+2bh+2hl
  =2(lb + bh + hl)
  For a cube of side 2cm;
  A =2(3x2²)
  =24 cm²

Example

Find the surface area of a triangular prism shown below.

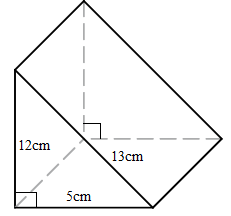
Area of the triangular surfaces = ½ x 5 x 12 x 2cm²
=60 cm²
Area of the rectangular surfaces=20 x 13 +5 x 20 +12 x 20
=260 + 100 + 240 = 600cm²
Therefore, the total surface area= (60+600) cm²
=660 cm²

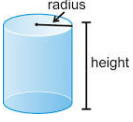
Cylinder

• A prism with a circular cross-section is called a cylinder, see the figure below.
  
  
• If you roll a piece of paper around the curved surface of a cylinder and open it out, you will get a rectangle whose breath is the circumference and length is the height of the cylinder. The ends are two circles. The surface area S of a cylinder with base and height h is therefore given by;
  S=2πrh + 2πr²

Example

Find the surface area of a cylinder whose radius is 7.7 cm and height 12 cm.

Solution

S =2π(7.7) x 12 + 2π(7.7)² cm²
=2 π(7.7) x 12 + (7.7)² cm²
=2 x 7.7π (12 + 7.7) cm²
=2 x 7.7 x π(1 9.7) cm²
=15.4π (19.7) cm²
=953.48 cm²

Area of Irregular Shapes

The area of irregular shape cannot be found accurately, but it can be estimated. As follows;

1. Draw a grid of unit squares on the figure or copy the figure on such a grid, see the figure below
   
   
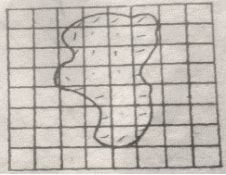
2. Count all the unit squares fully enclosed within the figure.
3. Count all partially enclosed unit squares and divide the total by two, i.e.., treat each one of them as half of a unit square.
4. The sum of the numbers in (ii) and (ii) gives an estimate of the areas of the figure.
   From the figure, the number of full squares is 9
   Number of partial squares= 18
   Total number of squares = 9 + ¹⁸/₂
   =18
   Approximate area = 18 sq. units.

Past KCSE Questions on the Topic

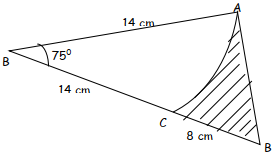
1. Calculate the area of the shaded region below, given that AC is an arc of a circle centre B. AB=BC=14cm CD=8cm and angle ABD = 75⁰ (4 mks)
   
   
2. The scale of a map is 1:50000. A lake on the map is 6.16cm². find the actual area of the lake in hactares. (3mks)
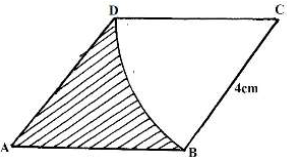
3. The figure below is a rhombus ABCD of sides 4cm. BD is an arc of circle centre C. Given that ∠ABC = 138⁰. Find the area of shaded region. (3mks)
   
   
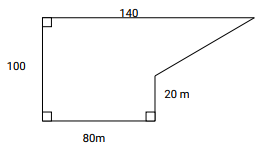
4. The figure below sows the shape of Kamau’s farm with dimensions shown in meters
   Find the area of Kamau’s farm in hectares (3mks)
   
   
5. In the figure below AB and AC are tangents to the circle centre O at B and C respectively, the angle AOC = 60⁰
   
   Calculate
   1. The length of AC
      
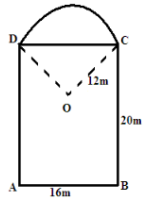
6. The figure below shows the floor of a hall. A part of this floor is in the shape of a rectangle of length 20m and width 16m and the rest is a segment of a circle of radius 12m. Use the figure to find
   
   
   1. The size of angle COD (2mks)
   2. The area of figure DABCO (4mks)
   3. Area of sector ODC (2mks)
   4. Area of the floor of the house. (2mks)
7. The circle below whose area is 1 8.05cm2 circumscribes a triangle ABC where AB = 6.3cm, BC = 5.7cm and AC = 4.8cm. Find the area of the shaded part
   
   
8. In the figure below, PQRS is a rectangle in which PS=1 0k cm and PQ = 6k cm. M and N are midpoints of QR and RS respectively
   
   
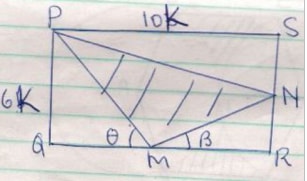
   1. Find the are of the shaded region (4 marks)
   2. Given that the area of the triangle MNR = 30 cm². find the dimensions of the rectangle (2 marks)
   3. Calculate the sizes of angles and giving your answer to 2 decimal places (4 marks)
9. The figure below shows two circles each of radius 10.5 cm with centres A and B. the circles touch each other at T. 
   
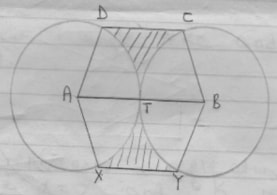
   Given that angle XAD =angle YBC = 160⁰ and lines XY, ATB and DC are parallel, calculate the area of:
   1. The minor sector AXTD (2 marks)
   2. Figure AXYBCD (6marks)
   3. The shaded region (2 marks)
10. The floor of a room is in the shape of a rectangle 1 0.5 m long by 6 m wide. Square tiles of length 30 cm are to be fitted onto the floor.
    1. Calculate the number of tiles needed for the floor.
    2. A dealer wishes to buy enough tiles for fifteen such rooms. The tiles are packed in cartons each containing 20 tiles. The cost of each carton is Kshs. 800. Calculate
       1. the total cost of the tiles.
       2. If in addition, the dealer spends Kshs. 2,000 and Kshs. 600 on transport and subsistence respectively, at what price should he sell each carton in order to make a profit of 12.5% (Give your answer to the nearest Kshs.)
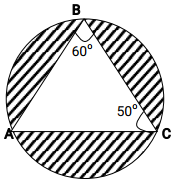
11. The figure below is a circle of radius 5cm. Points A, B and C are the vertices of the triangle ABC in which ∠ABC = 60^o and ∠ACB=50^o which is in the circle. Calculate the area of ∠ABC
    
    
12. Mr.Wanyama has a plot that is in a triangular form. The plot measures 1 70m, 1 90m and 21 0m, but the altitudes of the plot as well as the angles are not known. Find the area of the plot in hectares
13. Three sirens wail at intervals of thirty minutes, fifty minutes and thirty five minutes. If they wail together at 7.18a.m on Monday, what time and day will they next wail together?
14. A farmer decides to put two-thirds of his farm under crops. Of this, he put a quarter under maize and four-fifths of the remainder under beans. The rest is planted with carrots. If 0.9acres are under carrots, find the total area of the farm