Uniform Circular Motion Questions and Answers - Physics Form 4 Topical Revision

Questions

1. A light inextensible string of length L is fixed at its upper end and support a mass m at the other end. m is rotated at horizontal plane or radius r as shown. The maximum tension the string can withstand without breaking is 2N. Assuming the string breaks when the radius is maximum, calculate the velocity of the mass when the string breaks, given that L = 1.25m, and m= 0.1kg.
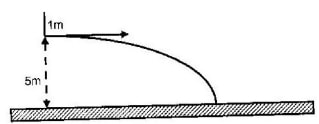
2. The diagram below shows a mass m, which is rotated in a vertical circle. 
   The speed of the mass is gradually increased until the string breaks. The string breaks when the mass is at its lowest position A and at a speed of 30ms^-1. Point a is 5m above the ground.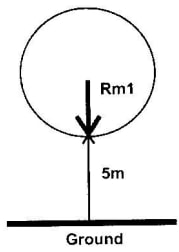
   
   
   1. Show on the diagram.
      1. The initial direction of the mass at the point the string breaks.
      2. The path of the mass from A until it strikes the ground at a point b.
   2. Calculate;
      1. The time the mass takes to reach the ground after breaking off.
      2. The horizontal distance the mass travels before it strikes the ground.
      3. The vertical velocity with which the mass strikes the ground.
3. State the principle by which a speed governor limits the speed of a vehicle.
4. The rear wheel of a certain car has a diameter of 40cm. At a certain speed of the car, the wheel makes 7 revolutions per second. A small stone embedded in the tyre tread flies off initially at an angle of 450 to the ground. Determine the initial velocity of the pebble (take π = ²²/₇)
5.  
   1. Explain why a pail of water can be swung in a vertical circle without the water pouring out.
   2. A car of mass 1,200kg is moving with a velocity of 25m/s around a flat bend of radius 150m. Determine the minimum frictional force between the tyres and the road that will prevent the car from sliding off.
6.  
   1. The fig shows the diagram of a set up to investigate the variation of centripetal force with the radius r of the circle in which a body rotates. Describe how the set up can be used to carry out the investigation
      
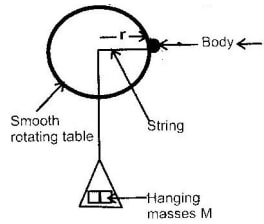
   2. The table shows results obtained from an investigation similar to the one in part (a)
      

      Mass, m (g)	60	50	40	30	20
      Radius, r(cm)	50	41	33	24	16

      1. Plot a graph of force, F (y-axis) on the body against the radius r (in metre)
      2. Given that the mass of the body is 100g, use the graph to determine the angular velocity.
7. A small object moving in a horizontal circle of radius 0.2m makes 8 revolutions per second. Determine its centripetal acceleration.
8.  
   1. Define the term angular velocity. (1mk)
   2. A body moving with uniform angular velocity found to have covered an angular distance 170 radians in t seconds. Thirteen seconds later it is found to have covered a total angular distance of 300 radians. Determine t (3mks)
   3. The figure below shows a body of mass m attached to the centre of rotating table with a string whose tension can be measure. (This device for measuring the tension is not shown in the figure).
      
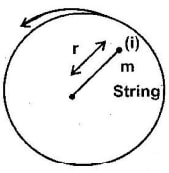
      The tension, T, on the string was measured for various values of angular velocity, 
      The distance r of the body from the centre was maintained at 30cm. Table 1 shows the results obtained.
      Table 1
      

      Angular velocity (rads-1)	2.0	3.0	4.0	5.0	6.0
      Tension T (N)	0.04	0.34	0.76	1.30	1.96

      (5mks)
      1. Plot the graph of T (y-axis) against ω²
      2. From the graph, determine the mass, m, of the body given that T= mω²r − C where C is a constant (4mks)
      3. Determine the constant C and suggest what it represents in the set up. (2mks)
9. A child of mass 20kg sits on a swing of length 4m and swings through a vertical height of 0.9m as shown in the figure below.
   
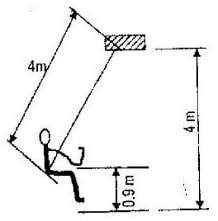
   Determine the:
   1. Speed of the child when passing through the lowest point.
   2. Force exerted on the child by the seat of the swing when passing through the lowest point.
10.  
    1. State what is meant by centripetal acceleration?
    2. The figure below shows masses A, B and C placed at different points on a rotating table.
       The angular velocity, ω of the table can be varied.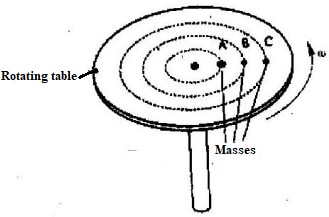
       
       
       1. State two factors that determine whether a particular mass slides off the table or not. (2mks)
       2. It is found that masses slide off at angular velocities ω_A, ω_B, ω_C of in decreasing order. (1mk)
    3. A block of mass 200g is placed on a frictionless rotating table while fixed to the centre of the table by a thin thread. The distance from the centre of the table to the block is 15cm. If the maximum tension the thread can withstand is 5.6N, determine the maximum angular velocity the table can attain before the thread cuts. (4mks)
11. Find the maximum speed with which a car of mass 100kg can take a corner of radius 20m if the coefficient of friction between the road and the tyres is 0.5.
12. An object of mass 0.5kg is rotated in a horizontal circle by a string 1m long. The maximum tension in the string before it breaks is 50N. Calculate the greatest number of revolutions per second the object can make.
13. An astronaut is trained in a centrifuge that has an arm length of 6m. If the astronaut can stand the acceleration of 9g. What is the maximum number of revolutions per second that the centrifuge can make?
14. A small body of 200g revolves uniformly on a horizontal frictionless surface attached by a cord 20cm long to a pin set on the surface. If the body makes two revolutions per second. Find the tension of the cord.
15. A circular highway curve on a level ground makes a turn 90^0. The highway carries traffic at 120 km/h. Knowing that the centripetal force on the vehicle is not to exceed ¹/₁₀ of its weight, calculate the length of the curve
16. A turntable of record player makes 33 revolutions per minute. What is the linear velocity of a point 0.12m from the center?
17. An object 0.5kg on the end of a string is whirled around in a vertical circle of radius 2m, with a speed of 10m/s. What is the maximum tension in the string?

Answers

1. When tension is max then r= l
   T= F = MV²
               r
   2 = 0.1 x V²
           1.25
   ∴ V² = 2 x 1.25 
               0.1
   V= 5 m/s
2.  
   1. (i) & (ii)
      
   2.  
      1. S= Ut + ½ at²
         t = √(2 x 5)
                  10
         = 1 seconds
      2. S = Ut = 30 x 1 = 30m
      3. V² = U² + 2as
         V= √(2 x 10 x 5)
           = 10m
3. Principal of conical pendulum Or principle of circular motion
4. V= ωr
   But ω = θ = 2π x 7 = 14 rads^-1
               T        1
   ∴ V= 14πx 0.20
   = 8.8 m/s
5. Centripetal acceleration of bucket is equal or higher than gravitational acceleration of the water.
6.  
   1. Keep angular velocity ω₁ constant; Centripetal force provided by mg; Fix the mass m and measure r; repeat for different values of m. Tabulate the values
   2.  
      1. Force- Mg. Calculate and fill a column for force and another for radius in m
         Plot the graph
      2. Gradient of the graph
         =   0.625 – 0.1   = 1.167 N/m
             0.525 – 0.075
         Force F, on the body = m_bω²r
         Where m_b = mass of the body
         M_bω² = Gradient of the graph = 1.167
         ω² = 1.167 = 11.67
                   0.1
         ω= √11. 67
         = 3.42 rads^-1
7. 2πf = 2π x 8
   α = rω² = 0.2 (16π)²
   = 505.3 m/s
8.  
   1. Angular displacement per second.
   2. In 13s, angle turned = 300 − 170 = 130 rad
      ∴ ω= ^θ/_t = ¹³⁰/₁₃ = 10 rads^-1
      So   300 = 10
            t+13
      10t + 130 = 300
      10t = 170
      t = 17 sec
   3.  
      1. Plot the graph which is a straight line.
      2. From T = (mr)ω² – C and y = mx + c
         Y = T, grad = mr, y = intercept = -C
         ∴ Obtain gradient and equate it to mr.
         Where r = 0.3m, to obtain m.
      3. The y-intercept should be equated to, -C.
9.  
   1. Pe → Ke
      ∴ mgh = ½ mv²
      Or v² = 2gh.
      v = √(2x 10x0.9)
      v = √18 = 1.24m/s
   2. F = mg + mv²
      = 200 + 20 x 18
                       4
      = 290N
10.  
    1. Acceleration directed towards the centre of the orbit.
    2.  
       1. Roughness/smoothness of surface, radius of path, angular velocity/speed.
11. 10 m/s
12. 1.59 rev.s^-1
13. 0.61 rev.s^-1
14. 6.32N
15. 1744N
16. 0.41 m/s
17. 30N