KCSE 2014 Physics Paper 1 Questions with Marking Scheme

Share via Whatsapp

« Previous Topic
KCSE 2014 Business Studies Paper 2 Questions with Marking Scheme

Next Topic »
KCSE 2014 Physics Paper 2 Questions with Marking Scheme

Download PDF for future reference Get on Whatsapp for 50/-

QUESTIONS

SECTION A: (25 marks)
Answer ALL questions in the spaces provided.

A student measured the length of a wire four times using a metre rule and obtained the following readings: 18.6 cm; 18.5 cm; 18.6 cm and 18.5 cm. Determine the length the student should record. (2 marks)
Figure 1 shows a magnified scale of a micrometer screw gauge.

Record the reading indicated. (1 mark)
State the reason why it is not correct to quote the weight of solid objects in kilograms. (1 mark)
Figure 2 shows a section of curved surface ABCD. Point A is higher than point B while BCD is horizontal. Point ABC is smooth while CD is rough. A mass m is realeased from restt A and moves towards D.

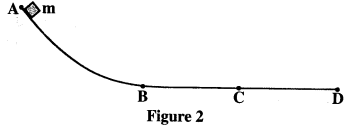
State the changes in the velocity of m between:
1. B and C (1 mark)
2. C and D (1 mark)
Figure 3 shows two cylinders of different cross-sectional areas connected with a tube. The cylinders contain an incompressible fluid and and are fitted with pistons of cross-sectional areas 4 cm² and 24 cm².

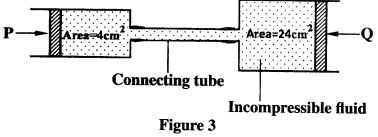
Opposite forces P and Q are applied to the pistons such that the pistons do not move. If the preassure on the smaller piston is 5 N cm². Determine the force Q. (2 marks)
An oil drop of volume V m³ introduced on the surface of water spreads to form a patch whose area is A m². Derive an expression for obtaining the diameter, d of a molecule of oil. (2 marks)
Figure 4 shows a source of heat placed at equal distances from two itentical flasks X and Y containing air. The surface of X is painted black while Y is clear.

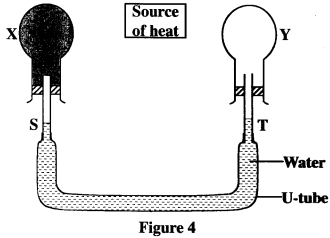
X and Y are linked by a U-tube filled with water whose levels are S and T are initially the same.
It is later observed that S falls while T rises. Explain this observation. (2 marks)
Figure 5 shows a uniform rod 4 m long and of mass 2 kg. It is pivoted 1 m from one end and ballanced horizontally attached to another string near the other end.

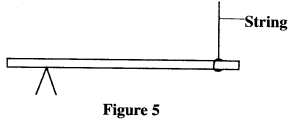
Determine the position where a mass of 5 kg should be placed on the rod so that the rod remains horizontal and the tension in the string is zero. (3 marks)
Figure 6 shows two identical rods JK and LK connected with a hinge at K.

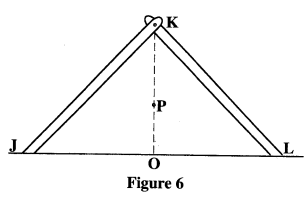
The position of the centre of gravity for the system is at P. The arrangement is now adjusted so that J and L move equal distances towards O. Sketch the new arrangement on the same diagram and mark the new position of the centre of gravity. (2 marks)
A light spiral spring extends by 4 mm when loaded with a weight W. The spring is connected in series with an identical spring. The combination is loaded with the weight W. Determine the extension of the combination. (2 marks)
Figure 7 shows an incompressible fluid flowing through a pipe, A₁ and A₂ are respectively cross-sectional areas of the pipes in the larger section and smaller section of the pipe respectively, while V₁ and V₂ are speeds of the fluids at the two sections of the pipe.

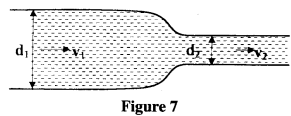
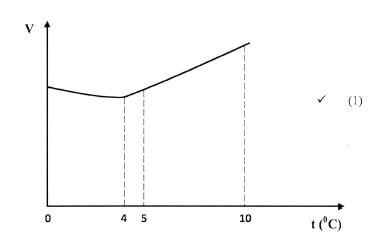
Derive an expression fot the ratio of speeds V₂/V₁ in terms of A₁ and A₂. (2 marks)
On the axis provided, sketch the graph which shows the relationship between volume and temperature of a fixed mass of water in the temperature range of 0⁰C to 10⁰C. (1 mark)
Figure 8 shows a graph of the variation of temperature with time for a pure substance heated at a constant rate.

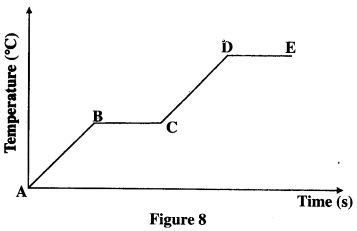
Assuming that heat transfer to the surroundings is negligible, state the changes observed the substance in region:
1. BC; (1 mark)
2. DE. (1 mark)
In a smoke cell experiment to demonstrate Brownian motion, smoke particles are seen moving randomly. State the cause of the randomness. (1 mark)

SECTION B: (55 marks)
Answer all questions in this section in the spaces provided.
Figure 9 shows a velocity-time graph for the motion of a body of mass 2 kg.
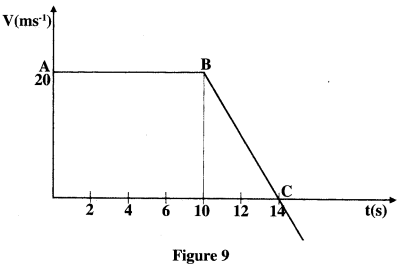
1. Use the graph to determine the:
  1. displacement of the body after 8 seconds. (3 marks)
  2. acceleration after point B; (3 marks)
  3. force acting on the body in part (a) (ii). (3 marks)
2. Sketch a displacement-time graph for the motion from point A to C. (2 marks)
Figure 10 shows a trolley of weight 20 N pulled by a force of 4 N from the bottom to the top of an inclined plane at a uniform speed.
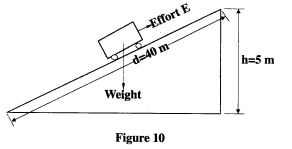
1. 1. State the value of the force acting downwards along the inclined plane. (1 mark)
  2. Explain how the value in part (a) (i) is obtained. (2 marks)
2. For the system, determine the:
  1. mechanical advantage; (3 marks)
  2. velocity ratio; (3 marks)
  3. efficiency. (2 mark)
1. A long horizontal capillary tube of uniform bore sealed at one end contains dry air trapped by a drop of mercury. The length of the air column in 142 mm at 17⁰C. Determine the length of the air column at 25⁰C. (3 marks)
2. The pressure of the air inside a car tyre increases if the car stands out in the sun for some time on a hot day. Explain the pressure increase in terms of kinetic theory. (3 marks)
3. In an experiment to determine the specific latent heat of vapourization of water, steam of mass 10 g at 100⁰C is passed into 100 g of water initially 20⁰C in a container of negligible heat capacity. The temperature of the water rises to 70⁰C.
  (Take the specific heat capacity of water at 4.2 x 10³ Jkg^-1 K^-1and the boiling point of water at 100⁰C)
  1. Determine the specific latent heat of vapourization of water. (4 marks)
  2. State two sources of error in this experiment. (2 marks)
1. When a bus goes round a bend on a flat road, it experiences a centripetal force.
  State what provides thhe centripetal force. (1 mark)
2. State the purpose of banking roads at bends. (1 mark)
3. A student whirls a stone of mass 0.2 kg tied to a string of length 0.4 m in a vertical plane at constant speed of 2 revolutions per second.
  (Take acceleration due to gravity g as 10 ms^-2)
  1. State two forces acting on the stone when it is at the highest point. (2 marks)
  2. Determine the;
    1. angular velocity of the stone; (3 marks)
    2. tension in the string when the stone is at the highest point; (1 mark)
Figure 11 shows a test-tube whose cross-sectional area is 2 cm² partially filled with lead shot floating vertically in water.

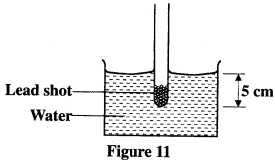
(Take gravitational acceleration as 10 ms^-2 and density of water ρ_w as 1 g cm^-3)
1. 1. Determine the:
    1. volume of the water displaced; (2 marks)
    2. weight of the water displaced. (3 marks)
  2. State the combined weight of the test-tube and the lead shot. (1 mark)
  3. Determine the length of the test-tube that would be submerged in a liquid of density 0.8 g cm^-3. (4 marks)
2. (b) The set up in figure 11 can be used as a hydrometer to measure densities of liquids. State how such a hydrometer would be improved to measure small differences in densities of liquids. (1 mark)

Marking Scheme

L = 18.6 +18.5 + 18.6 + 18.5
4
L = 74.2 = 18.55
4
students should record 18.6 cm
3.46 mm read from photograph.
Weight = Mass x gravity
OR (kilograms is the unit of measuring the mass and does not depict the force of gravity)
1. BC = Constant
2. CD - decreasing
F = p
A
F = 5 x 24
F = 120 N
Volume of drop = Volume of patch
Ad = V
d = V
A
Flask painted black absorbs more heat;
causing more expansion of air above S than above T;
hence S is pushed downwards and T upwards;
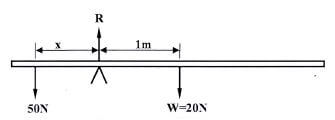
50 x = 20 x 1
x = 20
50
= 0.4 m
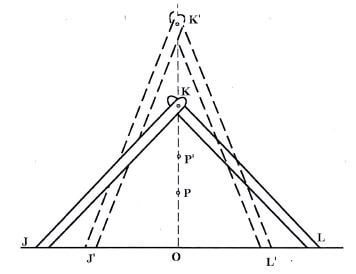
raised K to K¹
-P also raised to P¹
Extension = 4 mm + 4 mm
= 8 mm
A₁V₁ = A₂V₂
V₂= A₁V₁A₂
1. BC - Solid changes to liquid
2. DE - Liquid changes to vapour
Collisions / bombardment of particles with air molecules which are in random motion.
1. 1. Displacement = Area under graph
    = 20 x 8 m
    = 160 m (3 marks)
  2. After point B,
    a = 0 - 20 = - ms^-2
    4
    = -5 ms^-2
  3. F = ma = 2 x -5 N
    = -10 N (3 marks)
1. 1. Force = 4 N
  2. Since velocity is constant. (uniform speed)
    Resultant force is zero = Force downwards is equal to force upwards
    = 4N
2. 1. M. A = load = 20
    Effort 4
    = 5
  2. V. R = effort distance
    load distance
    = 40
    5
    = 8
  3. Efficiency =M.A x 100%
    V.R
    =5 x 100
    8
    =62.5%
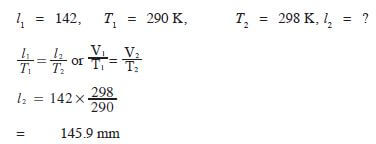
2. In the hot sun the temperature of the air increases; therefore the speed of the air molecules increases hence the rate of collisions between the molecules and tyre increases; The rate of change of momentum (pressure) of the molecules also increases.
3. 1. Heat lost = Heat gained
    mLv + M∆θC_steam = M∆θC_water
    0.01 Lv + 0.01 x 30 x 4200 = 0.1 x 4200 x 50
    0.01 Lv = 21000 - 1260
    Lv = 19740
    0.01
    =1.974 x 10⁶JKg^-1K^-1
  2. All the heat lost by the steam is not absorbed by the water alone.
    Reading the thermometer at wrong meniscus resulting in wrong temperatures.
1. Friction between road and tyre.
2. Increases the centripetal force acting on the bus.
3. 1. Weight
    Tension
  2. 1. f = 2 revolutions / sec
      T = 2π = 1
      ω f
      f = ω = 2
      2π
      ω = 2 × 2π
      = 4πrad S^-1 = 12.56
      13 rad S^-1
    2. T + mg = mrω²
      T = mrω² -mg
      = 0.2 × 0.4 (16π²) - 0.2 × 10
      = 10.63
      = 10.6N
1. 1. 1. Volume of water displaced = 2 × 5
      = 10 cm³
    2. Mass = Volume × density
      = 10 × 1
      = 0.01 kg
      therefore: weight = 0.01 × 10
      = 0.1 N
  2. Combined weight = upthrust
    = 0.1 N
  3. Weight of liquid displaced = 0.1N
    Mass of liquid displaced = 0.01 kg = 10 g
    Volume of liquid displaced = mass = 10
    density 0.8
    = 12.5 cm³therefore: Length submerged = 2 L= 12.5
    (C.S A × L = volume)
    0.8 L = 10
    L = 10
    0.8
    = 6.25 cm
2. Use a narrower test tube.