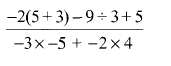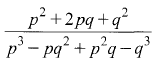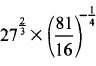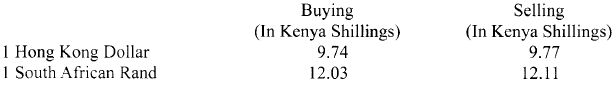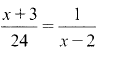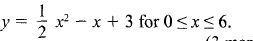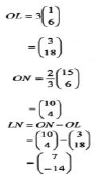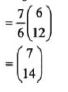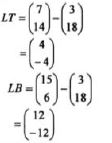SECTION I (50 marks)
Answer all the questions from this section in the spaces provided.
- Without using a calculator evaluate, (3marks)
- Simplify (4 marks)
- The external length, width and height of an open rectangular container are 41 cm, 21cm and 15.5 cm respectively. The thickness of the materials making the container is 5 mm. If the container has 8 litres of water, calculate the internal height above the water level. (4 marks)
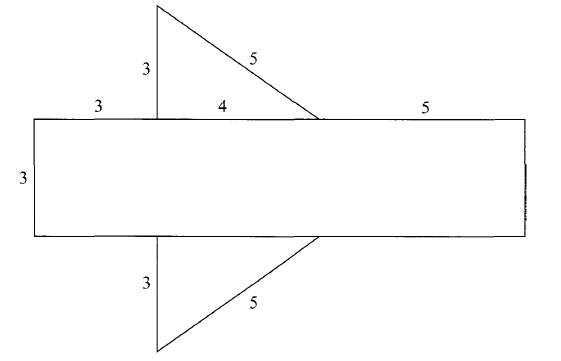
- The figure below shows a net of a solid (measurements are in centimetres).
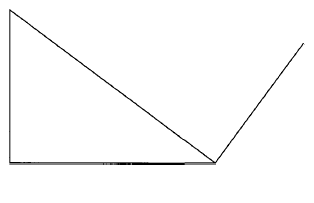
Below is a part of the sketch of the solid whose net is shown above. Complete the sketch of the solid, showing the hidden edges with broken lines. (3 marks) - Given that OA = 2i + 3j and OB = 3i — 2j, find the magnitude of AB to one decimal place. (3 marks)
- A bus travelling at an average speed of 63 km/h left a station at 8:15 a.m. A car later left the same station at 9:00 a.m. and caught up with the bus at 10:45 a.m. Find the average speed of the car. (3 marks)
- Given that x is an acute angle and cos x° = 2/5√5 find, without using mathematical tables or a calculator, tan (90 — x)°. (2 marks)
- Without using mathematical tables or a calculator, evaluate (3 marks)
- A minor arc of a circle subtends an angle of 105° at the centre of the circle. If the radius of the circle is 8.4 cm, find the length of the major arc. (Take π it = 22/7). (3 marks)
- The gradient of the tangent to the curve y= — ax3 + bx at the point (1,1) is —5. Calculate the values of a and b. (4 marks)
- A line with gradient of —3 passes through the points (3, k) and (k, 8). Find the value of k and hence express the equation of the line in the form ax + by — c, where a, b and c are constants. (3 marks)
- Points L and M are equidistant from another point K. The bearing of L from K is 330°. The bearing of M from K is 220°. Calculate the bearing of M from L. (3 marks)
- In this question, mathematical tables should not be used.
A Kenyan bank buys and sells foreign currencies as shown below:
A tourist arrived in Kenya with 105 000 Hong Kong Dollars and changed the whole amount to Kenya Shillings. While in Kenya, she spent Sh 403 879 and changed the balance to South African Rands before leaving for South Africa. Calculate the amount in South African Rand, that she received. (3 marks)
- A small cone of height 8 cm is cut off from a bigger cone to leave a frustum of height 16 cm. If the volume of the smaller cone is 160 cm3, find the volume of the frustum. (3 marks)
- The production of milk, in litres, of 14 cows on a certain day was recorded as follows:
22, 26, 15, 19, 20, 16, 27, 15, 19, 22, 21, 20, 22 and 28.
Determine:- the mode: (1 mark)
- the median. (2 marks)
- Given that Log 4 = 0.6021 and Log 6 = 0.7782, without using mathematical tables or a calculator, evaluate log 0.096. (3 marks)
SECTION II (50 marks)
Answer any five questions from this section in the spaces provided.
-
- Solve the equation (4 marks)
- The length of a floor of a rectangular hall is 9 m more than its width. The area of the floor is 136 m2.
- Calculate the perimeter of the floor. (4 marks)
- A rectangular carpet is placed on the floor of the wall leaving an area of 64 m2. If the length of the carpet is twice its width, determine the width of the carpet (2 marks)
- Solve the equation (4 marks)
- Three business partners: Asha, Nangila and Cherop contributed Ksh 6 000, Ksh 85 000 and Ksh 105 000 respectively. They agreed to put 25% of the profit back into business each year. They also agreed to put aside 40% of the remaining profit to cater for taxes and insurance. The rest of the profit would then be shared among the partners in the ratio of their contributions. At the end of the first year, the business realised a gross profit of Ksh 225 000.
- Calculate the amount of money Cherop received more than Asha at the end of the first year. (5 marks)
- Nangila further invested Ksh 25 000 into the business at the beginning of the second year. Given that the gross profit at the end of the second year increased in the ratio 10:9, calculate Nangila’s share of the profit at the end of the second year. (5 marks)
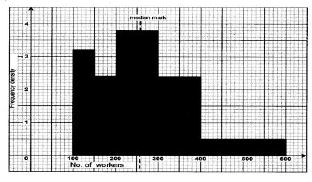
- The frequency table below shows the daily wages paid to casual workers by a certain company.
Wages in shillings 100-150 150-200 200-300 300-400 400-600 No. of workers 160 120 380 240 100 - In the grid provided, draw a histogram to represent the above information. (5 marks)
-
- State the class in which the median wage lies. (1 mark)
- Draw1 a vertical line, in the histogram, showing where the median wage lies. (1 mark)
- Using the histogram, determine the number of workers who earn Sh 450 or less per day. (3 marks)
- In the grid provided, draw a histogram to represent the above information. (5 marks)
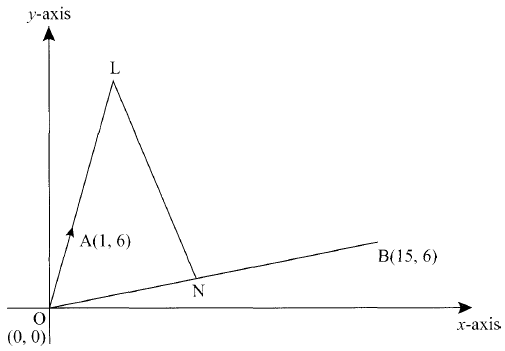
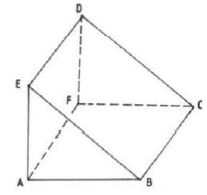
- In the diagram below, the coordinates of points A and B are (1, 6) and (15, 6) respectively. Point N is on OB and that 30N = 20B. Line OA is produced to L such that OL = 30A
- Find vector LN. (3 marks)
- Given that a point M is on LN such that LM:MN = 3:4, find the coordinate of M. (2 marks)
- If line OM is produced to T such that OM:MT = 6:1
- Find the position of vector T (1 mark
- Show that points L, T and B are collinear. (4 marks)
-
- The ratio of Juma’s and Akinyi’s earnings was 5:3. Juma’s earnings rose to Ksh 8 400 after an increase of 12%.
Calculate the percentage increase in Akinyi’s earnings given that the sum of their new earnings was Ksh 14 100. (6 marks) - Juma and Akinyi contributed all the new earnings to buy maize at Ksh 1175 per bag. The maize was then sold at Ksh 1762.50 per bag. The two shared all the money from the sales of the maize in the ratio of their contributions. Calculate the amount that Akinyi got. (4 marks)
- The ratio of Juma’s and Akinyi’s earnings was 5:3. Juma’s earnings rose to Ksh 8 400 after an increase of 12%.
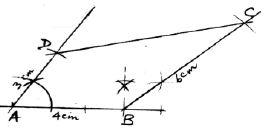
- Using a pair of compasses and ruler only, construct:
-
- Triangle ABC in which AB = 5 cm, <BAC = 30° and <ABC = 105°. (3 marks)
- A circle that passes through the vertices of the triangle ABC. Measure the radius. (3 marks)
- the height of triangle ABC with AB as the base. Measure the height. (2 marks)
- Determine the area of circle that lies outside the triangle correct to 2 decimal places. (2 marks)
-
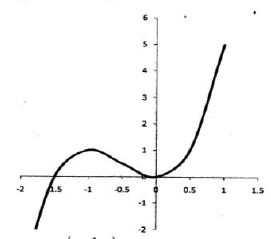
- The equation of a curve is y = 2x3 + 3x2.
- Find:
- the x-intercept of the curve: (2 marks)
- the y-intercept of the curve. (1 mark)
- Determine the stationary points of the curve. (3 marks)
- For each point in (b) (i) above, determine whether it is a maximum or a minimum. (2 marks)
- Sketch the curve. (2 marks)
- Find:
-
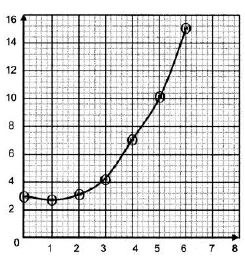
- On the grid provided, draw a graph of the function (3 marks)
- Calculate the mid-ordinates for five strips between x = 1 and x = 6, and hence use the mid-ordinate rule to approximate the area under the curve between x = 1, x = 6 and the x - axis. (3 marks)
- Assuming that the area determined by integration to be the actual area, calculate the percentage error in using the mid-ordinate rule. (4 marks)
- On the grid provided, draw a graph of the function (3 marks)
MARKING SCHEME
- -2(5+3)-9+3+5 = -14 = -2
-3x-5+(-2)x4 7 - (p+q)(p+q)
p(p2-q2)+q(p2-q2)
(p+q)(p+q)
(p+q)(p+q)(p-q)
= 1
p-q - Internal Dimensions: 40,20, and 15
Volume unoccupied= 40 x 20 x 15 - 8000
=4000
Height above water level= 4000/40x20=5cm -
- Distance covered by bus= 63 x (10.45 - 8.15)
= 63 x 2.5
=157.5
Speed of car
= 157.5
1.75
= 90km/h - l2 = 52 - (2√52)=5
l=√5
∴ tan(90-x)º= 2√5/√5 or 2 - 272/3 x (81/16)1/4 = (33)2 x (34/24)1/4
=32 x (3/2)-1
=32 x 2/3
=6 - Angle of major arc= 360 - 105= 255
length of arc = 255/360 x 2 x 8.4 x 22/7
=37.4cm - dy/dx = 3ax2 + b
3a+b=-5
a+b=1
a=-3
b=4 - k-8 = -3
3-k 1
k-8 = -9 +3k
2k 1
k = ½
y-8 = -3
x-½ 1
y-8 = -3(x -½)
y-8= -3x + 3/2
2y-16= 6x+3
6x+2y=19 - <LKM=110º
<KLM=35º or KML=35º
Bearing =185º - 105000 x 9.74
= sh1022700
1022700 - 403879
12.11
= 618821
12.11
=51100 rands - L.S.F= 8:24= 1:3
V.S.F= 1:27
Volume of frustrum= 160 x 27 - 160
=4160cm3 -
- mode =22
- Median
15,15,16, 19,19, 20, 20, 21, 22,22,22, 26, 27, 28
median = 20 + 21/2
= 20.5
- Log 0.096= Log ( 42 x 6 x 10-3)
= 2( 0.6021) + ‾3.7782
=‾2.9824 or
(-1.0176) -
- x = 5 or -6
- 50m
- 6m
-
- % profit for taxes and insurance
= 40 x 75
100 100
amount shared
= 100 - (25 + 30) x 225000
100
= 45/100 x 225000
= 101250
amount cherop received more than Asha: ratio of contribution
60000: 85000: 105000
12 : 17 : 21
21- 12 x 101250
50
= 18225 - profit during 2nd year
225000 x 10/9
= 250000
Nangila's new ratio
= 110000 = 2
275000 5
∴ Nangila's new share profit
= 2/5 x 112500
= 45000
- % profit for taxes and insurance
-
-
Frequency (f) 160 120 380 240 100 Class width(c) 50 50 100 100 200 Freq density(f/c) 3.2 2.4 3.8 2.4 0.5 - Median class= 200-300
- Shown by dotted line ( 257.875)
- Number of workers who earn sh 450 or less per day = 900 + 50 x 0.5 = 925
-
-
-
- OM= OL + 3/7 LN
=M(6,12) -
- OT=7/6OM
-
LB=3LT
L is the common point
- OT=7/6OM
-
-
- Juma's earnings before increase
112% → 8400
100% → 8400 x 100/112 = 7500
Akinyi's earnings before increase:
3/5 x 7500 = 4500
Increase in Akinyi's earningws
14100 - 8400 - 4500 = 1200
% increase in Akinyi's earnings
1200/4500 x 100
= 26 2/3 - No. of bags bought
14100/ 1175
=12 bags
profit = (1762.50 - 1175) x 12 = 7050
Ratio 5700:8400 = 19:28
Profit for Akinyi= 7050 x 19/47 = 2850
Total earning for Akinyi
5700 + 2850= 8550
- Juma's earnings before increase
-
construction of 135º angle between lines AB=4cm and BC=6cm
Construction of 60º angle between lines AB=4cm and AD=3cm
Completion of quadilateral ABCD= <BCD = 31º ± 1º -
-
- x- intercepts
when y=0
x2(2x+3)=0
x=0 and x = -3/2 - y - intercept
when x =0, y=0
- x- intercepts
-
- Stationary points of curve
dy/dx = 6x2 + 6x
stationary points when dy/dx = 0
ie 6x2 + 6x = 0
6x( x + 1)= 0
x=0 or x=-1
∴ stationary points are
(0,0) and (-1, 1) -
x -2 -1½ -1 -½ 0 ½ 1 dy/dx 12 4½ 0 -1½ 0 4½ 12
minimum poin t(0,0)
maximum point (-1,1)
- Stationary points of curve
-
points are at ( -1½, 0), (-1, 1) and (0,0)
smooth curve
-
-
x 0 1 2 3 4 5 6 y=½x2-x+3 3 2½ 3 4½ 7 10½ 15
Download KCSE 2016 Mathematics Paper 1 Questions with Marking Scheme.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students