PHYSICS PAPER 3 - 2020 KCSE PREDICTION SET 1 (QUESTIONS AND ANSWERS)

Question one

1. You are provided with the following apparatus
   - A lens
   - Lens holder
   - Candle
   - Screen
   - A screen with a hole having cross-wire
   - Metre rule

   Proceed as follows

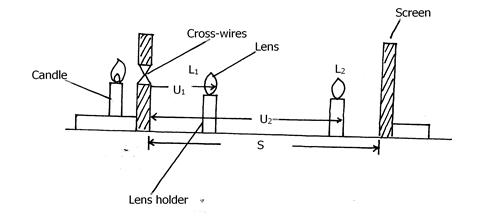
   1. Set up the apparatus as in the figure below with distance S = 42cm
      
      Without changing the distance S move the lens slowly away from cross-wires until a sharp enlarged inverted image is formed on screen position L₁. Measure the distance U₁ from cross-wires to the lens and record this value in table 2. Keeping distance S, constant move the lens away from cross-wires to a new position L₂ where a small sharp inverted image is formed on the screen. Measure the new object distance U₂ and record in table 2. Determine the displacement d of the lens from L₁ to L₂ (i.e d = L₂ – L₁)
   2. By setting the distance S to distances 44, 46, 48, 50 and 52cm as shown in table 2 repeat procedure (a). Measure and record the corresponding values of U₁ and U₂ in table 2
      Table 2 (10mks)
      

      S (cm)	42	44	46	48	50	52
      U1 (cm)
      U2 (cm)
      d (U2 – U1) (cm)
      d2 (cm2)
      S2 (cm2)
      S2 – d2 (cm2)

   3.  
      1. Plot graph of S² – d² against S                                                                        (5mks)
      2. Determine the slope of the graph                                                                    (3mks)
      3. Given that S² – d² = 4fS, use your graph to determine the focal length of the lens   (2mks)

QUESTION TWO

2. You are provided with the following:
   - a metre rule;
   - a retort stand, a boss and clamp;
   - three pieces of thread;
   - 200m1 of a liquid in a 250ml beaker labelled W;
   - 200m1 of a liquid in a 250m1 beaker labelled L;
   - Two masses labelled m₁ and m₂.

   Proceed as follows:

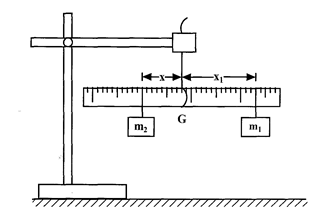
   1. Suspend the metre rule so that it balances at its centre of gravity G and record its value
      
      G = .................................................................................cm                                        (½mk)
   2. Position mass m₂ at a distance x = 5 cm from the centre of gravity G and adjust the position of m_l so that the metre rule balance at G. Record the x₁ of m₁ from the point G in table 2.
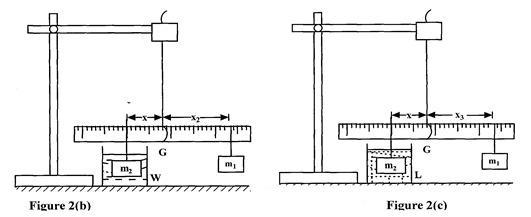
   3. While maintaining the distance x = 5cm, immerse m₂ completely in water. Adjust the position of m₁ until the metre rule balances again (see figure 2(b)). 
      Record the new distance x₂.
      
      
   4. Still maintaining the same distance x = 5cm, remove the beaker, W with water and replace it with the beaker L with the liquid. Immerse m₂ completely in the liquid. Adjust the position of m_l until the metre rule balances again (see figure 2(c)). Record the new distance x₃.
   5. Remove mass m₂ from the liquid and dry it with a tissue paper.
   6. With the metre rule still suspended from its centre of gravity G, repeat the procedure in (b), (c), (d) and (e) for other values of x given in table 2. Complete the table.
      TABLE 2
      

      Distance x (cm)	Distance x1 (cm)	Distance x2 (cm)	Distance x3 (cm)	L0 = (x1 – x2) (cm)	L1 = (x1-x3) (cm)
      5
      10
      15
      17
      20

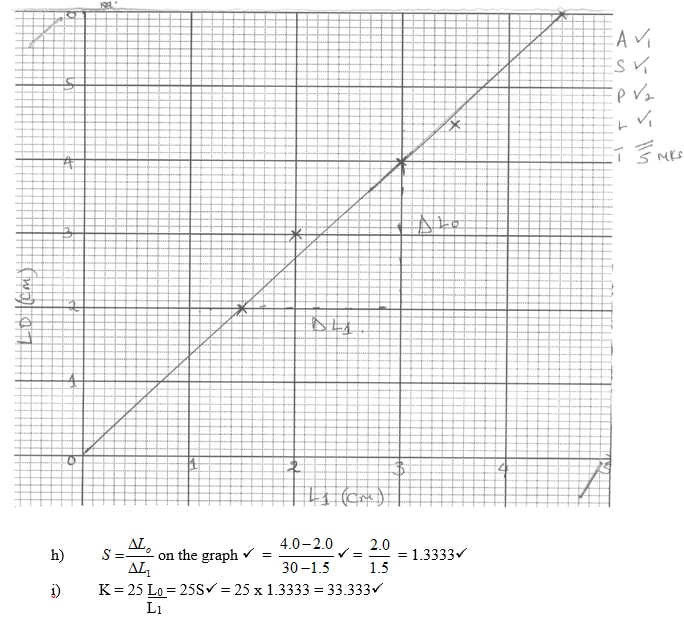
   7. Plot a graph of L₀(y-axis) against L₁                                                                           (5mks)
   8. Find the slope S of the graph.                                                                         (3mks)
   9. Find the value of k given that L₁ = ²⁵/_K      (2mks)

MARKING SCHEME

1.  
   2.  
      

      S (cm)	42	44	46	48	50	52
      U1 (cm)	16.0	15.0	15.0	14.0	14.0	13.0	(3mks)
      U2 (cm)	25.0	28.0	31.0	33.0	36.0	38.0	(3mks)
      d = (U2 – U1) (cm)	9.0	13.0	16.0	19.0	22.0	25.0	(1mk)
      d2 (cm2)	81	169	256	361	484	625	(1mk)
      S2 (cm2)	1764	1936	2116	2304	2500	2704	(1mk)
      S2 – d2(cm2)	1683	1767	1860	1943	2016	2079	(1mk) (10mks)

      
      
      
   3.  
      1.  
         
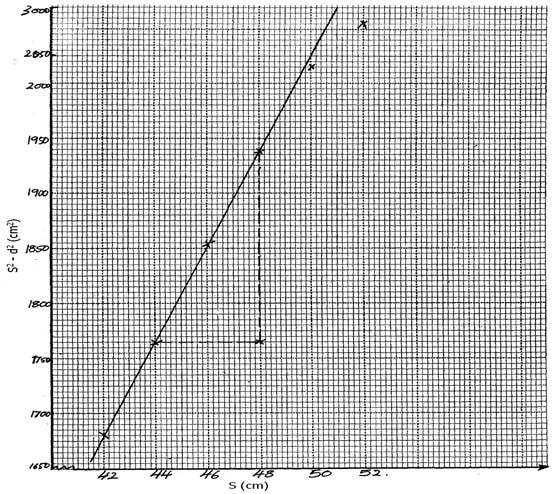
      2. Slope = (1945 – 1770)cm² = 175cm = 43.75cm
                         (48 – 44)cm            4            (3mks)
      3. S² – d² = 4fs
         y = nx
         4f = slope
         f = slope = 43.75 = 10.9cm
                 4            4            (2mks)

2.  
   1. G = 50.0 + 1cm √ ½MK  (49.0 – 51.0) ----MUST BE IN 1dp
      

      x (cm)	x1 (cm)	x2 (cm)	x3 (cm)	L0 (cm)	L1 (cm)
      5.0	10.0	8.0	8.5	2.0	1.5
      10.0	21.0	18.0	19.0	3.0	2.0
      15.0	31.0	27.0	28.0	4.0	3.0
      17.0	35.5	31.0	32.0	4.5	3.5
      20.0	42.0	36.0	37.5	6.0	4.5
      	√ ½ each	√ ½ each	√ ½ each	√ ½ max of 1mk	√ ½ max of 1 mk       Total 9½mks

   2.