Physics Paper 1 Questions and Answers - KCSE Prediction Papers 2022

Instructions to Candidates

This paper consists of TWO sections: A and B. Answer ALL the questions.
ALL working MUST be clearly shown.
Mathematical tables and non-programmable silent electronic calculators may be used.

Questions

SECTION A (25 Marks)
Answer all the questions in this section in the spaces provided

The level of water in a burette is at 30cm³. 400 drops of water each of volume 0.015cm³ was removed from the burette. Determine the new level of water in the burette (3 mks)
Calculate the temperature change of water as it falls through a height of 20 m. (Take g = 10 N/kg and s.h.c of water = 4200 J/kg/K) (3 mks)
State the SI unit of density (1 mk)
Give a reason why heat transfer by radiation is faster than heat transfer by conduction (1 mk)
A railway truck of mass 4000 kg moving at 3 m/s collides with a stationary truck of mass 2000 kg. The couplings join and the trucks move off together. Calculate their common velocity after collision. (3 mks)
State the principle of moments (1 mk)
An air bubble with a volume of 1cm³ escapes from the helmet of a diver at a depth of 200 m below the water surface. What will be the volume of the bubble immediately it breaks the surface of water? (Take atmospheric pressure = 10 m of water) (4 marks)
Calculate the acceleration due to gravity on a planet where an object released from rest falls through a height of 54.2 m in 1.08 s. (3 mks)
State the three factors on which the rate of heat flow depends on. (3 mks)
Under a driving force of 3000 N, a car of mass 1200 kg has an acceleration of 1.3m/s². Find the frictional resistance acting in the car. (3 mks)

SECTION B (55 marks)
Answer ALL the questions in this section in spaces provided

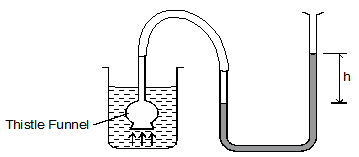
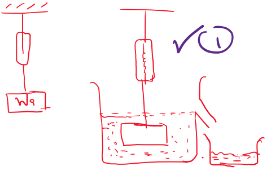
1. The diagram below shows a set up used by a student to show variation of pressure in a liquid. The thistle funnel is wrapped with an elastic membrane.
  
  State and explain the effect on the height, h, when the thistle funnel is moved upwards towards the surface of the liquids. (2 marks)
2. Figure below shows a simple barometer.
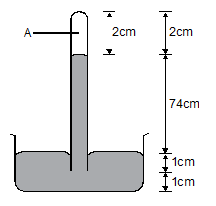
  1. What name is given to region A? (1 mk)
  2. What keeps the mercury in the tube? (1 mk)
  3. What is the value of the atmospheric pressure shown?(1 mk)
  4. What would happen to the value in (iii) if it taken up a high mountain? (1 mk)
  5. Give a reason for (iv) above. (1 mk)
1. In opening a door, the moment exerted about the hinges was 15Nm. If the pushing force was 25N and perpendicular to the door, what is the distance of the force from the hinges? (2 mks)
2. A uniform plank of wood is balanced 30cm from one end when a lead of 0.08kg is hung at one end as shown below. Calculate the weight of the plank. (2mks)
3. State two factors that affect centre of gravity. (2 mks)
1. Sketch a velocity-time graph of a ball dropped to the ground and caught when it bounces up again. (2 mks)
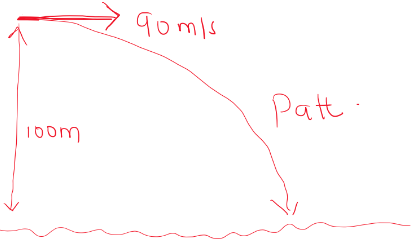
2. In areas of the world where a plane is unable to land free fall airdrops can be used to deliver supplies. A plane travelling at a speed of 90m/s and a height of 100m releases a load of supplies. (g=10N/kg)
  1. Sketch the path followed by the falling load. (1 mk)
  2. Find the horizontal distance of the load from the drop zone to where it landed (3mks)
3. Define the Newton. (1 mk)
4. The reading on a speedometer of a car of mass 1000kg is 60km/hr when the brakes are applied. The car is brought to rest in 10m. Find;
  1. The retardation. (2 mks)
  2. Find the average breaking force. (2 mks)
1. The figure below shows the motion of a ticker tape through a ticker-timer whose frequency is 100Hz.
  
  Determine:
  1. Velocity at AB and PQ (2 mks)
  2. Acceleration of the tape. (2 mks)
2. State two factors that affect centripetal force of a body moving a circular path. (2 mks)
3. A stone of mass 1.2 kg is tied to a rope and whirled in a vertical circle of radius 3.2m with a speed of 6.32m/s. Calculate
  1. The centripetal acceleration of the stone. (2 mks)
  2. The tension in the rope when the stone is at the highest point. (2 mks)
1. State the law of floatation. (1 mk)
2. You are provided with the following
  - A block of wood.
  - A spring balance.
  - A thin thread.
  - Overflow can
  - A small measuring cylinder.
  - Some liquid.
    With the aid of a labelled diagrams describe an experiment to verify the law of floatation. (4 mks)
3. A block of length 80cm, cross sectional area 3.0cm² and density 1300kg/m³ is completely immersed in a liquid of density 1030kg/m³. Determine
  1. The mass of the block. (1 mk)
  2. The weight of the block in the liquid. (3 mks)
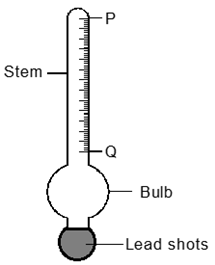
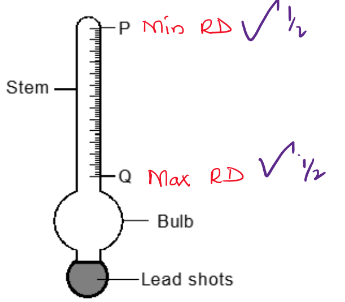
4. The diagram below shows a car acid hydrometer.
  1. Mark on the diagram maximum and minimum measurements to be taken.(1 mk)
  2. State the reason why the bulb is wide.(1 mk)

1. State Charles law. (1 mk)
2. A gas of volume 2m³ at 27°C is cooled to -123°C, at constant pressure. What is its new volume? (2 mks)

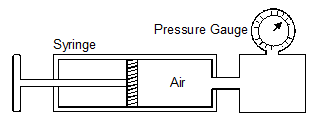
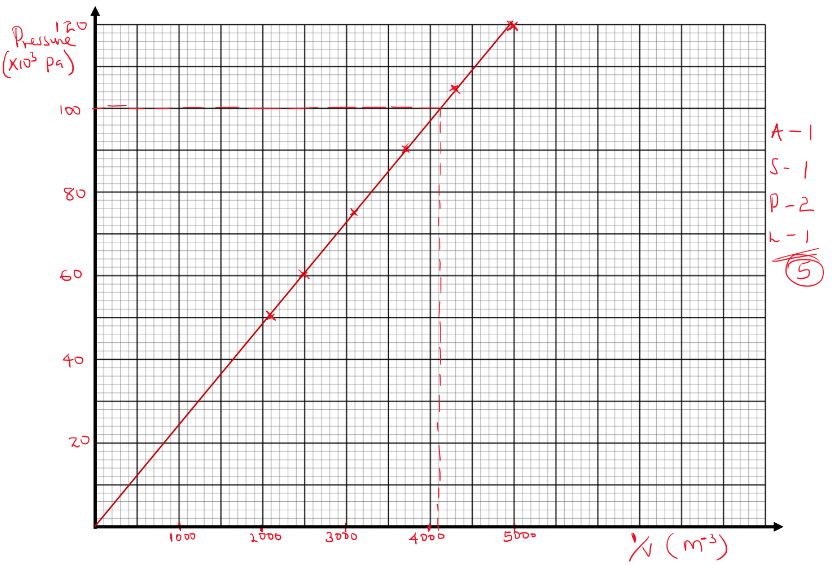
The figure shown illustrates an apparatus in which a fixed mass of air was compressed in a calibrated syringe, which was approximately half full of air at atmospheric pressure and a temperature of 17°C corresponding values of volume and pressure of the trapped air as shown in the table.

Pressure (Kpa)	50	60	75	90	105	120
Volume (cm³)	0.00048	0.00040	0.00032	0.00027	0.00023	0.00020
¹/_volume(¹/_v)		2500		3704

Complete the table by filling values for ¹/_Vsome values have been entered. (1 mk)
Plot a graph of pressure against ¹/_V,with pressure on the y-axis.(5 mks)
What relationship between pressure and volume of the trapped air can be deducted from your graph? Explain your answer. (1 mk)
If the temperature of air was increased to 27°C, what would happen to the volume occupied by the air at a pressure of 100Kpa? (1 mk)

Marking Scheme

SECTION A (25 Marks)
Answer all the questions in this section in the spaces provided

The level of water in a burette is at 30cm³. 400 drops of water each of volume 0.015cm³ was removed from the burette. Determine the new level of water in the burette (3 marks)
volume of drop = ( 400 × 0.015)
=6cm³
New level = 30+ 6 = 36cm³
Calculate the temperature change of water as it falls through a height of 20 m. (Take g = 10 N/kg and s.h.c of water = 4200 J/kg/K) (3 marks)
GPE = Heat gain
mgh = mcΔθ
10 × 20 = 4200 × Δθ
Temperature change; Δθ = 0.0476°C
State the SI unit of density (1 mark)
- Kilogram per cubic metre (Don't award symbol)
Give a reason why heat transfer by radiation is faster than heat transfer by conduction (1 mark)
- Radiation is propagated by means of electromagnetic waves while conduction is by movement of particles which is prone to distractions through collisions.
A railway truck of mass 4000 kg moving at 3 m/s collides with a stationary truck of mass 2000 kg. The couplings join and the trucks move off together. Calculate their common velocity after collision. (3 marks)
m₁u₁ = m₂u₂ = (m₁ + m₂)u
4000 × 3 + 0 = 6000v
v = 2m/s
State the principle of moments (1 mark)
- For a system in equilibrium the sum of clockwise moments about a point is equal to the sum of anticlockwise moments about the same point.
An air bubble with a volume of 1cm³ escapes from the helmet of a diver at a depth of 200 m below the water surface. What will be the volume of the bubble immediately it breaks the surface of water? (Take atmospheric pressure = 10 m of water) (4 marks)
P₁V₁ = P₂V₂
1 × (200 + 10) = (10 × P₂)
10 P₂ = 210
10 10
p = 21cm³
Calculate the acceleration due to gravity on a planet where an object released from rest falls through a height of 54.2 m in 1.08 s. (3 marks)
S = ut + ½gt²
54.2 = 0 + ½ × g × 1.08²
g = 54.2
0.5832
= 92.94m/s²
State the three factors on which the rate of heat flow depends on. (3 marks)
- Temperature difference
- Area of cross-section
- The length of the conductor
- Nature of the material
Under a driving force of 3000 N, a car of mass 1200 kg has an acceleration of 1.3m/s². Find the frictional resistance acting in the car. (3 marks)
F = ma
= 1200 × 1.3
= 1560N
Friction = 3000 − 1560 = 1440N

SECTION B (55 marks)
Answer ALL the questions in this section in spaces provided

1. The diagram below shows a set up used by a student to show variation of pressure in a liquid. The thistle funnel is wrapped with an elastic membrane. Use it to answer the question that follow.
  
  State and explain the effect on the height, h, when the thistle funnel is moved upwards towards the surface of the liquids.
  - The height h reduces
  - Pressure actinig on the trapped gas reduces with depth
2. Figure below shows a simple barometer.
  1. What name is given to region A?
    - Torricelian Vaccum
  2. What keeps the mercury in the tube?
    - The atmospheric pressure
  3. What is the value of the atmospheric pressure being shown by the barometer?
    - 74cmHg
  4. What would happen to the reading if the barometer was taken up a high mountain.
    - The reading will reduce
  5. Give a reason for (d) above.
    - The pressure is low and therefore a shorter column of mercury is supported.
1. In opening a door, the moment exerted about the hinges was 15Nm. If the pushing force was 25N and perpendicular to the door, what is the distance of the force from the hinges?
  moment = F × d
  ¹⁵/₂₅ = ²⁵/₂₅d
  d = 0.6m
2. A uniform plank of wood is balanced 30cm from one end when a lead of 0.08kg is hung at one end as shown below. Calculate the weight of the plank.
  
  Clockwise moment = Anticlockwise moments
  w × 25 = 0.08 × 10 × 30
  25w = 24
  w = 0.96N
3. State two factors that affect centre of gravity.
  - The position of the centre of gravity.
  - The area of support( base area)
1. Sketch a velocity-time graph of a ball dropped to the ground and caught when it bounces up again.
2. In areas of the world where a plane is unable to land free fall airdrops can be used to deliver supplies. A plane travelling at a speed of 90m/s and a height of 100m releases a load of supplies. (g=10N/kg)
  1. Sketch the path followed by the falling load.
  2. Find the horizontal distance of the load from the drop zone to where it landed.
    h = ½gt²
    100 = ½ × 10 × t²
    t² = 20
    t = 4.472s
    Range = ut
    = 90 × 4.472
    = 402.48m
3. Define the Newton.
  - Is the force that gives a mass of 1 kilogram an acceleration of 1 metre per square second.
4. The reading on a speedometer of a car of mass 1000kg is 60km/hr when the brakes are applied. The car is brought to rest in 10m. Find;
  1. The retardation.
    u = 60 × ⁵/₁₈
    = 16.67 m/s
    v² = u² + 2as
    O = 16.67² + 2 ×10a
    20a = −277.89
    a = −13.89 m/s²
    Retard = 13.89 m/s²
  2. Find the average breaking force.
    F = ma
    = 1000 × − 13.89 (ignore the negative)
    = 13890N
1. The figure below shows the motion of a ticker tape through a ticker-timer whose frequency is 100Hz.
  
  Determine:
  1. Velocity at AB and PQ
    V_AB = 12
    2 × 0.01
    V = 600cm/s
    V_PQ= 32
    2 × 0.01
    V = 1600cm/s
  2. Acceleration of the tape.
    a = v − u
    t
    = 600 − 1600
    6 × 0.01
    a = 16666.67cm/s²
    = 166.67m/s²
2. State two factors that affect centripetal force of a body moving a circular path.
  - The radius of the curve
  - The linear velocity of the body
  - Mass of the body
3. A stone of mass 1.2 kg is tied to a rope and whirled in a vertical circle of radius 3.2m with a speed of 6.32m/s. Calculate
  1. The centripetal acceleration of the stone.
    a = v²
    r
    = 6.32²
    3.2
    a = 12.482 m/s²
  2. The tension in the rope when the stone is at the highest point.
    T = mv² − mg
    r
    = 1.2 × 12.48 − 1.2 × 10
    T = 14.98 − 12
    = 2.98N
1. State the law of floatation.
  - Floating body displaces its own weight of the fluid in which it floats.
2. You are provided with the following
  - A block of wood.
  - A spring balance.
  - A thin thread.
  - Overflow can
  - A small measuring cylinder.
  - Some liquid.
    With the aid of a labelled diagrams describe an experiment to verify the law of floatation.
  - Suspend the block and measure its weight in air.
  - Suspend the cylinder and get its weight.
  - Now suspend the block in overflow can and collect the overflow in a measuring cylinder.
  - Measure the wieght of the cylinder together with water.
  - weight of block in air = weight in water collected
3. A block of length 80cm, cross sectional area 3.0cm² and density 1300kg/m³ is completely immersed in a liquid of density 1030kg/m³. Determine
  1. The mass of the block.
    m = vp
    = 80 × 3 × 1.3
    = 312g
  2. The weight of the block in the liquid.
    u = pvg
    = 1030 × 0.8 × 3 × 10⁻⁴ × 10
    = 2.472N
    W_L = ³¹²/₁₀₀ = 2.472
    = 0.648N
4. The diagram below shows a car acid hydrometer.
  1. Indicate on the diagram the maximum and minimum measurements to be taken. (1 mark)
  2. State the reason why the bulb is wide.
    - To displace more volume thus increasing upthrust ∴ making the hydrometer float more.

1. State Charles law.
  - The volume of a fixed mass of a gas is directly proportional to its absolute temperature provided the pressure remains constant.
2. A gas of volume 2m³ at 27°C is cooled to -123°C, at constant pressure. What is its new volume?
  V₁ = V₂
  T₁ T₂
  2 = V₂
  300 150
  V₂ = ²/₃₀₀ × 150
  V₂ = 1m³

Pressure (Kpa)	50	60	75	90	105	120
Volume (cm³)	0.00048	0.00040	0.00032	0.00027	0.00023	0.00020
¹/_volume	2083	2500	3125	3704	4348	5000

Complete the table by calculating values for ¹/_Vsome of the values have been entered for you.
Plot a graph of pressure on the y-axis against ¹/_Von the x- axis.
What relationship between pressure and volume of the trapped air can be deducted from your graph? Explain your answer.
- Pressure is directly proportional to ¹/_V .
- The graph is a straight line.
If the temperature of air was increased to 27°C, what would happen to the volume occupied by the air at a pressure of 100Kpa?
- The volume would increase.