INSTRUCTIONS TO CANDIDATES
- This paper consists of two sections A and B.
- Answer ALL questions in sections A and B in the spaces provided.
- All working must be clearly shown
- Non programmable silent calculators may be used.
For Examiner’s use only
|
SECTION |
QUESTION |
MAXIMUM SCORE |
CANDIDATES’ SCORE |
|
A |
1 - 11 |
25 |
|
|
B |
12 |
11 |
|
|
13 |
10 |
||
|
14 |
13 |
||
|
15 |
11 |
||
|
16 |
10 |
||
|
|
TOTAL |
80 |
|

QUESTIONS
SECTION A: (25 MARKS)
- The vernier callipers shown below has a zero error of 0.06cm.
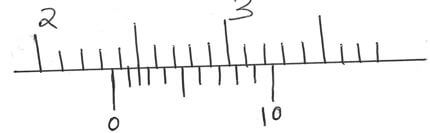
State the actual reading on the instrument. (2 marks) - State with a reason the role of the vacuum in a thermos flask (2 marks)
- A wooden bench and a metal bench are both left overnight outside. State with a reason which bench feels colder to touch in the morning. (2 marks)
- The figure below shows an empty wine glass
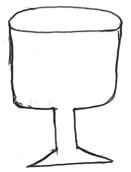
State and explain the effect on its stability when water is put into the glass. (2 marks) - The figure below shows three identical springs which obeys Hooke’s law. The pans of the second and the third springs are also identical.
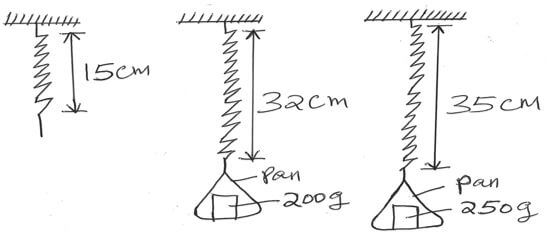
Determine the mass of the pan. (3 marks) - A ball bearing falling through glycerine attains terminal velocity after a short time. State the reason why it attains terminal velocity. (2 marks)
- Using Kinetic theory of matter, explain why gases are easily compressible while liquids and solids are not. (1 mark)
- The figure below shows a mercury manometer attached to a gas supply.
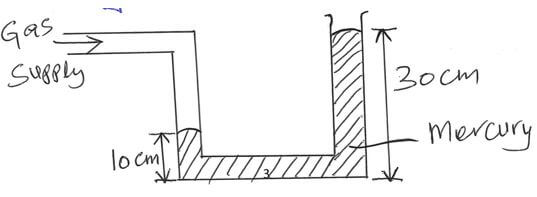
If the atmospheric pressure is 103360Pa, calculate the pressure due to the gas. (Take density of mercury as 13600kg/m3 and g=10N/kg). (3 marks) - When a mercury thermometer is used to measure the temperature of hot water, it is observed that the mercury level first drops before beginning to rise. Explain (2 marks)
- The figure below shows a uniform metre rule pivoted and supported as shown below. The rule is in equilibrium.

If the mass of the rule is 2.4Kg. Find the distance X. (3 marks) - A balloon is filled with air to a volume of 200ml at a temperature of 27ºC. Determine the volume when the temperature rises to 67ºC at the same pressure. (3 marks)
SECTION B: (55 MARKS)
-
- State the Law of floatation. (1 mark)
- A block of wood measuring 8 cm by 5cm by 20cm floats in a liquid of density 800kg/m3 with the longest side vertical as shown below.
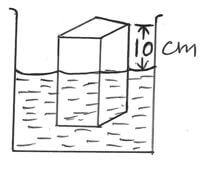
Determine- The upthrust exerted by the liquid on the block. (3 marks)
- The density of the block (3 marks)
- You are provided with the following; a test tube, some sand, kerosene, water and a beaker. Describe an experiment on how you would make a hydrometer to measure relative densities in the range of 0.8 – 1.0. (Density of wateris 1g/cm3 and density of kerosene is 0.8g/cm3) (4 marks)
-
- Define the term mechanical advantage of a machine (1 mark)
- The figure below shows a gear wheel system in which a load of 1800N can be raised by an effort of 800N.
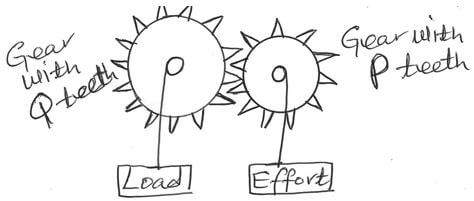
- Given that the effort gear has P number of teeth and the load gear with Q number of teeth. Show that the velocity ratio (V.R) for the system is given by Q⁄P (3 marks)
- If P=10 teeth and Q=30 teeth, calculate the efficiency of the system. (3 marks)
- If the Load is raised by 80cm, calculate the work that is required to be done on the system. (3 marks)
-
- State two ways in which the centripetal force on a body of mass M can be increased.(2 marks)
- The figure below shows an object of mass 200g at the end of a string 120cm long being whirled round a vertical circle in the direction shown.
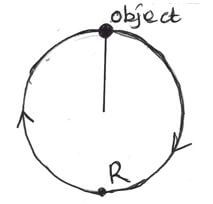
- State two forces acting on the object at any instant as it continues to move in the vertical circle. (2 marks)
- Indicate with an arrow on the figure the direction of;
- Centripetal force (1 mark)
- Velocity at the position shown. (1 mark)
- State the reason why the object is accelerating while its speed remains constant. (1 mark)
- If the object makes 3 revolutions per second
Determine:- Angular velocity of the stone (3 marks)
- The tension of the string at point R, the lowest point (3 marks)
-
- Define the term specific latent heat of fusion. (1 mark)
- In an experiment to determine the specific latent heat of vaporisation of water, steam at 100oC was passed into water contained in a well lagged alluminium calorimeter. The following measurements were made.
- Mass of calorimeter = 100g
- Initial mass of water = 150g
- Initial temperature of water = 18ºC
- Final mass of calorimeter + water + condensed steam =264g
- Final temperature of mixture = 68ºC (Specific heat capacity of water = 4200J/kgK and specific heat capacity of alluminium = 400J/kgK).
- Determine
- Mass of the condensed steam. (1 mark)
- Heat gained by calorimeter and water (3 marks)
- Given that L is the specific latent heat of vaporisation of steam, calculate the value of L. (4 marks)
- Determine
- State two factors that affects the melting point of ice. (2 marks)
-
- A small Iron ball is dropped from the top of a vertical cliff and takes 2.5 seconds to reach the sandy beach.
Calculate- The velocity with which it strikes the sand. (2 marks)
- The height of the cliff (2 marks)
- If the ball above penetrates the sand to a depth of 12.5cm. Calculate the average retardation. (3 marks)
- State the Law of conservation of Linear momentum (1 mark)
- State two way of reducing friction force between moving parts of a machine. (2 marks)
- A small Iron ball is dropped from the top of a vertical cliff and takes 2.5 seconds to reach the sandy beach.

MARKING SCHEME
-
- Reading = 2.32 cm (1 mk)
- Actual reading = 2.32 cm - 0.06cm = 2.26 cm ( 1 mk)
-
-
- vacuum reduces heat transfer (gain or loss) by conduction and convection. ( 1mk)
- There is absence of material medium in the vacuum while both conduction and convection regquires a material medium( 1 mk)
-
-
- The metal bench ( 1 mk)
- The metal is a better conducrtor of heat than wood, it therefore conducts heat away from the body faster than the wood (1 mk)
-
- The stability reduces/decreases /lowers(1 mk)
- The position of center of gravity is raised because more mass is added to the upper part. (1 mk)
-
- Let the weight of the pan be x
Mass = 200g
Extension = 32 – 15 = 17 cm
K1 = F/e
= (x+2)/17
Mass = 250g
Extension = 35 – 15 = 20 cm
K2 = F/e
= (x+2.5)/20 ( 1 mk) For both k1 and k2
K1 = k2 since springs are identical
(x+2)/17 = (x+2.5)/20 ( 1 mk)
X = 0.833333333 N
Mass of the pan
W = mg
m = 0.8333/10
m = 0.08333 kg ( 1 mk)
m = 83.33 g
- Let the weight of the pan be x
-
- This is when the upwards forces equals the downwards forces(1 mk)
- The net ( resultant) force is zero/ the acceleration is zero ( 1 mk)
-
- Gases have larger intermolecular distances than in solids and in liquids
-
- pressure of the gas, Pg= Pa+ hρg (1 mk)
hρg = 20/100 X 13600 X 10
= 27,200N/m2 (1mk)
Pg= 103360 + 27200
= 130,560 N/m2 (1 mk)
- pressure of the gas, Pg= Pa+ hρg (1 mk)
-
- The bulb of the thermometer is heated first and expands, the level of the mercury falls. ( 1mk)
- Later, the mercury in the bulb is heated and expands more than the bulb, this makes the level of mercury to rise. ( 1 mk)
-
- clockwise moments = anticlockwise moments
OR F1d1= F1d1 ( 1 mk)
24 x 50 = 16( 100 – x) ( 1 mk)
1200 = 1600 – 16x
X = 25 cm ( 1 mk)
- clockwise moments = anticlockwise moments
-
- P1V1/T1 = P2V2/T2
T1 = 27 + 273 = 300K
T2 = 67 + 273 = 340K
P1 = P2 since pressure is constant
V1/T1 = V2/T2 (1mk)
200/300 = V2/340 (1mk)
V2 = 226.67 ml ( 1 mk)
- P1V1/T1 = P2V2/T2
-
- a floating object displaces its own weight of the fluid in which it floats. 1mk
-
- U = Vρg ( 1 mk)
= 8/100 X 5/100 X 10/100 X 800 X 10 ( 1 mk)
= 3.2 N ( 1mk) - density = mass/volume
W = 3.2 N since the object is floating
m = W/10
= 3.2/10
= 0.32 kg or 320 g ( 1 mk)
Density = 320/(8 x 5 x20) ( 1 mk)
= 320/800
= 0.4 g/cm3( 1 mk)
OR V = 8/100 X 5/100 X 20/100
= 8.0 X 10-4 m3
Density = 0.32/0.0008
= 400 kg/ m3
- U = Vρg ( 1 mk)
-
- put some sand into the testtube. ( 1mk)
- put some water into the beaker about 3⁄4 full.
- Dip the testtube with its contents into the water in the beaker.
- Mark the level of water on the testtube as 1. ( maximum). ( 1 mk)
- Pour the water from the beaker and replace it with kerosene about 3⁄4 full.
- Dip the testtube with its contents into the kerosene in the beaker. Mark the level of kerosene on the testtube as 0.8 ( minimum). ( 1 mk)
- Divide the interval in equal divisions to read relative densities in that range. ( 1 mk)
-
- Mechanical advantage is the ratio of Load to Effort. 1mk. Reject formula M.A=L/E
- V.R = (effort distance)/(load distance) ( 1 mk)
V.R = (revolutions made by the effort wheel ( gear))/(revolutions made by the load wheel ( gear)) ( 1 mk)
- if the effort gear makes 1 revolution, the load gear makes P/Q revolutions.
V.R = 1/(P/Q) ( 1 mk)
V. R = Q/P - V.R = Q/P
P = 10
Q = 30
V.R = 30/10
= 3 ( 1 mk)
M. A = L/E
= 1800/800
= 2.25 ( 1 mk)
Efficiency = (M.A)/(V.R) X 100
= 2.25/3 X 100
= 75 % ( 1 mk)
(Working of efficiency must be shown)
Work done by the system = F X d
= 1800 X 0.8
= 1440 J
Efficiency = (work done on the load)/(work done by the effort) X 100 ( 1 mk)
75 = X/1440 X 100 ( 1 mk)
X = 75/100 X 1440
X = 1080 J ( 1 mk)
- V.R = (effort distance)/(load distance) ( 1 mk)
- Mechanical advantage is the ratio of Load to Effort. 1mk. Reject formula M.A=L/E
-
-
- increasing the speed of rotation/increasing the rate of whirling/increasing frequency of rotation. (1 mk)
- reducing the radius of the circular path. ( 1mk)
-
- weight of the object ( 1mk)
- Tension in the string. ( 1mk
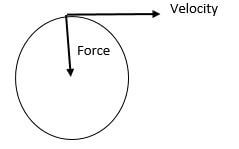
- There is change in the direction of the velocity because the direction of motion of the object changes with time. ( 1 mk)
-
- f = 3 Hz
Ѡ = 2πf ( 1 mk)
= 2 π X 3 ( 1 mk)
= 6 π
= 18.85 rad/s ( 1 mk) - T = mr Ѡ2 + mg ( 1 mk)
= 0.2 X 18.85 X 18.85 X 1.2 + 0.2 X 10
( 1 mk)
= 85.2774 + 2
= 87.28 N ( 1mk)
- f = 3 Hz
-
-
- specific latent heat of fusion is the amout of heat energy required to change the state of a unit mass of substance from solid state to liquid state without change in temperature. ( 1 mk)
-
-
- mass of condensed steam
= 264 – ( 150 + 100)
= 264 – 250
= 14 g ( 1 mk) - H = mccc∆θ + mwcw∆θ
= 100/1000 X 400 X 50 + 150/1000 X 4200 X 50
( 1 mk) ( 1 mk)
= 2000 + 31500
= 33500 J ( 1mk)
- mass of condensed steam
- heat lost = heat gained
heat lost by steam = 14/1000 X L + 14/1000 X 4200 X 32
( 1 mk)
= 0.014 L + 1881.6 ( 1 mk)
0.014L + 1881.6 = 33500 ( 1 mk)
0.014L = 31618.4
L = 31618.4/0.014
= 2,258,457.143 J /kg ( 1 mk)
– impurities (1 mk)
- pressure ( 1 mk)
-
-
-
- V = U + gt
V = 0 + 10 X 2.5
= 25 m/s ( 1 mk) - V2 = U2 + 2gs
25 X 25 = 0 x 0 + 2 X 10 X h
20h = 625
h = 31.25 ( 1 mk) - V2 = U2 + 2as
0 X 0 = 25 X 25 + 2 X a X 0.125
0 = 625 + 0.25a
a = - 2500m/s2 ( 1 mk)
retardation = 2500 m/s2 ( 1 mk)
- V = U + gt
- for a system of colliding bodies, the total linear momentum remains constant provided no external forces are acting. ( 1 mk)
-
- use of rollers
- use of ball bearings
- lubrication ( oiling or greasing )
( any two for 2 mk)
-
Download Physics Paper 1 Questions and Answers - Mathioya Mock 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

