Physics Paper 1 Marking Scheme - CATHOLIC DIOCESE OF KERICHO (CDK) EXAMS – 2018 PRE-MOCK WITH MARKING SCHEME

232/1
PHYSICS
PAPER 1
TIME: 2 HOURS

CATHOLIC DIOCESE OF KERICHO (CDK) EXAMS – 2018
PRE-MOCK
PHYSICS PAPER 1

INSTRUCTIONS TO THE CANDIDATES:

• Answer all the questions both in section A and B in the spaces provided below each question
• All workings must be clearly shown; marks may be awarded for correct steps even if the answers are wrong.
• Mathematical tables and silent electronic calculators may be used.
• Take acceleration due to gravity g=10ms^-2

SECTION A (25mks)
Answer all the questions in this section

1. The figure 1.0 below shows part of a vernier caliper:

   

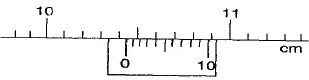
   1. What is the reading indicated by the scale? (1mk)
      M.S.R = 10.40
      V.S.R = ^0.04 / _10.44cm
      Reading = 10.44cm
      
      
   2. If the vernier caliper above had a zero error of 0.02cm, what is the diameter of the object measured above? (1mk)
      Zero error = +0.02cm
      Actual diameter = 10.44 - 0.02 = 10.42 cm
      
      
2. A piece of cotton thread is attached to a circular wire frame. The frame is dipped in soap solution and a soap film forms across the frame with the thread lying loosely in the film as shown in figure 2.0 below:

   

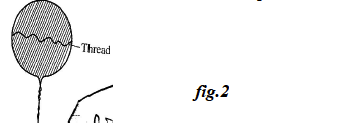
   The film is pricked with a sharp hot needle at a point above the string. Draw a diagram to show the shape of the film now. (1mk) Account for the shape you have drawn. (1mk)
   
   When one side of the film if prided, the surface tension acts only on one side of the thread; and it pulls the thread in such a way as to form circular arc.

3. Figure 3.0 below shows a rod made of wood on one end and metal on the other end suspended freely with a piece of thread so that it is in equilibrium; The side made of metal is heated with a Bunsen flame. State with reason the side to which the rod is likely to tip. (2mks)

   
   
   
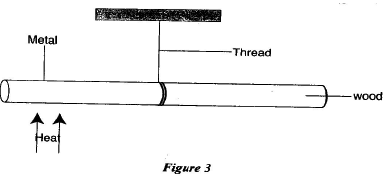
   The rod tips on the side with the metal. The balance point shifts to the side of the metal due to linear expansion

4. Explain why a bubble of air increases in volume as it rises from the bottom of a pond to the surface. (1mk)
   Pressure is highest at the bottom of the pond and it reduces as the depth reduces.
   
   
5. Oil is injected at a coastal town with a speed of 12m/s where the diameter of the pipe is 7cm, flows at some point inland where the radius of the pipe is 10.5cm. Determine the speed of the oil at this point. (3mks)
   
   
   
6. The figure 4.0 below shows a tape produced by a ticker timer whose frequency is 50Hz. 

   

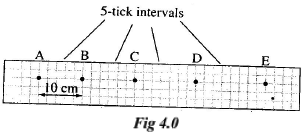
   Determine the acceleration of the body pulling the tape. Use the scale provided. (3mks)
   
   

   VAB = ^10cm/_0.1s =100cm/s
   VDE = ^16cm/_0.1s = 160cm/s

   a =^160-100 / _{3 x 0.1} = 200cm/s²

   = 2m/s²

7. State one factor that affect the constant of a spiral spring made using a wire of a given thickness and a certain material. (1mk)
   • Number of turns per unit length
   • Length of the spring
   • Diameter of the spring
     
     
8. Identify the force that provides for the centripetal force for an electron orbiting an atomic nucleus. (1mk)
   Electrostatic force
   
9. When a Bunsen burner is lit above a wire gauze it is observed that the flame initially burns above the gauze as shown in the figure 5(a) and 5(b) below. After sometime, the flame burns below as well as above the gauze as shown in figure 5(b) Explain the observation (2mks)

   
   
   
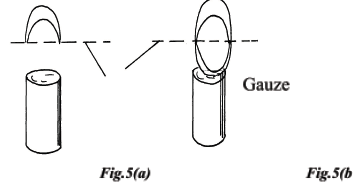
   The gauze gets heated and lights the gas below it.

    

10. What is the reason for milk ‘swelling’ and pouring when it is being boiled? (1mk)
    When the milk attains boiling point, further heating results in rapid vaporization of the milk which forms a foam-like state as it rises to spill. The swelling is a mixture of vapour and liquid
11. A student inverted a rounded flask with a glass tube and inserted it into water as shown in figure 6.0 below;

    

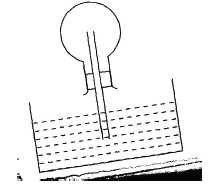
    1. When the student warmed the flask by rubbing it with his hands he noticed some bubbles escaping from the end of the tube into the water. Explain (1mk)
       

       Air in the flask expands when the flask absorbs heat from the hand thereby escaping from the flask into the water 

    2. What happens in the glass tube when the student stops rubbing and lets the flask to cool?(1mk)
       As the flask cools air contracts the water rises up the tube and into the flask.
       
       
       
12. Explain how you would change the weight of a body without changing its mass. (1mk)
    Moving to a location where the acceleration due to gravity is different.
    
    
13. It is easier to tighten and loosen nuts using a spanner with long handle than one with a short handle. Explain (1mk)
    Spanner with a longer handle produces a greater turning effect due to the increased perpendicular distance between the pivot and the line of action of force.
    
    
14. A uniform metre rule AB whose weight is 1.8N is suspended 40cm from B as shown in figure 7.0 below. A mass of 180g is suspended from the end B, while a block X is suspended 30cm from A. Determine the weight of the block X (3mks)

    
    
    

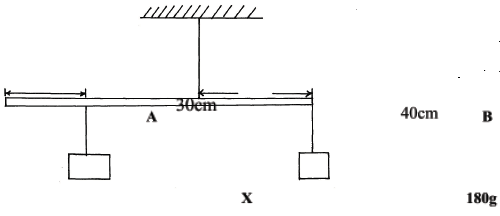
    Clockwise moments = Anticlockwise moments

    (30x X) + (1.8x10) = 1.8 x40)

    X = (40x1.8) – 1.8x10) 
                   30

    = 1.8N

SECTION B (55 MARKS)
Answer all questions in this section

15.  
    1.  
       1. Define the term centrifugal force. (1mk)
          The force equal and opposite to the centripetal force OR: The force that tends to pull the body away from the centre of the circle and equal to the centripetal force.
          
          
       2. A centrifuge containing muddy water being whirled at high speed is shown in figure below;

          

          Explain how the high speed rotation causes the separation of mud from water. (2mks)
          The suspended mud have a bigger mass and hence experience a higher centrifugal force; that force them to the bottom of the tube leaving clear water at the top.

    2. Explain why a body moving in a circular path with constant speed is said to be accelerating. (1mk)
       The direction of its velocity keeps on changing
       
    3. A wooden block of mass 200g is placed at various distances from the centre of a turntable, which is rotating at constant angular velocity. It is found that at a distance of 8.0cm from the centre, the block just starts to slide off the table. If the force of friction between the block and the table is 0.4N, calculate;
       1. The angular velocity of the table (3mks)
          

          F= mω²r √1mk
          0.4 = 0.2 x ω² x 0.08
          ω² = 0.4 √1mk
                 0.016
          ω= 5rads^-1 √1mk

       2. the force required to hold the block at a distance 12cm form the centre (2mks)
          

           F =mω²r = 0.2 x 5² x 0.12 √1mk
          = 0.6N √1mk

    4. A stone of mass 0.5Kg is whirled in a vertical circle with a constant speed of 4m/s tracing a circle of diameter 2.4m;

       

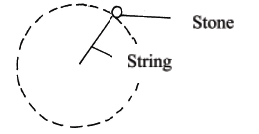
       Indicate on the diagram, the position at which the string would posses: (2mks)

       1. Maximum tension
       2. Minimum tension
16.  State the law of flotation (1mk)
    1. A floating body displaces its own weight of the fluid on which it floats.
       
    2. The figure below shows a rectangular metal block of density 10500Kg/m³ and dimensions 30cm by 20cm by 20cm suspended inside a liquid of density 1200Kg/m³ by a string attached to a point above the liquid. The three forces acting on the block are the tension T, on the string, the weight, W, of the block, and the upthrust, U, due to the liquid.

       

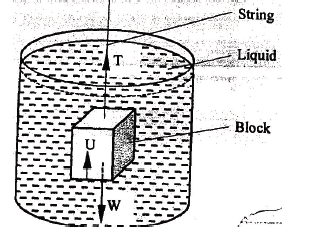
       1. Write the expression relating, T, W, and U when the block is in equilibrium inside the liquid. (1mk)
          W = T + U
       2. Determine the weight, W, of the block (3mks)
          

          V = 0.3 x 0.2 x0.2
          = 0.12m³ √1mk
          W= mg
          = 0.012 x 10500 x 10 √1mk
          = 1260N √1mk

       3. Determine the weight of the liquid displaced by the fully submerged block. (2mks)
          

          Vol. of liquid = vol. of block
          Weight of liquid displaced = Vρg
          = 0.3 x 0.2 x 0.2 x1200 x 10 √1mk =144N √1mk

       4. Hence determine the tension T, in the string (2mks)
          

          T = W – U
          = 1260 – 144 √1mk
          =1116N √1mk

    3. A certain solid of volume 50cm³ displaces 10cm³ of kerosene (density 800Kg/m³) when floating. Determine the density of the solid (3mks)
       
       

       Weight of solid = weight of kerosene displaced
       800 x 10 x 10^-6 = 0.08N √1mk
       Mass = 0.008Kg
       Vol. = 50cm³ √1mk
       Ρ = m = 0.008 = 160Kg/m³ √1mk

       V = 50 x 10^-6

17. 1. Define the term specific latent heat of vaporization (1mk)
       

       The quantity of heat required to change a unit mass of a material from liquid state to vapour without change of temperature.

    2. In an experiment to determine the specific latent heat of water, steam at 100^oC was passed into water contained in a well lagged copper calorimeter. The following measurements were made:
       Mass of calorimeter =50g
       Initial mass of water =100g
       Initial room temperature of water = 20^oC
       Final mass of water + calorimeter + condensed steam = 190g
       (Specific heat capacity of water = 4200JKg^-1K^-1)
       1. Determine the mass of condensed steam. (2mks)
          Mass of calorimeter + water = 50 + 100 = 150g √1mk
          Mass of condensed steam = 190 – 150 = 40g √1mk
          
          
       2. Find the heat gained by the calorimeter and water. (5mks)
       3. Given that Lv is the specific latent heat of vaporization of steam;
          1. write an expression for the heat given out by steam (1mk)
          2. Determine the value of Lv (3mks)
18. A fair ground ride trolley of mass 120Kg carrying two passengers of average mass 40Kg was released at point X of a frictionless curved surface S. upon reaching the horizontal, M collided with a stationery trolley N of mass 140Kg carrying three passengers of average mass 60Kg. if the two trolleys moved off together with a common velocity along the horizontal for 1.2 seconds before coming to rest, determine:

    

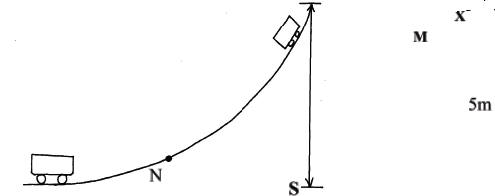
    1. The gravitational potential energy of trolley M when at point X (2mks)
       

       P.E = mgh
       = (120 + 2 x 40) x 10x5 √1mk
       =10,000J √1mk

    2. The velocity of M just before collision (3mks)
       

        

    3. The common velocity with which the two trolleys moved off along the horizontal after collisions (3mks)
       
       Mass of N = 140 + (3x60) =320Kg
       Momentum before collision= momentum after collision
       m₁u₁ + m₂u₂ = (m₁+m₂)v √1mk
       (2000x10) + (320x0) = (200+320) V
       2000 = 520V √1mk
       V= 3.85m/s √1mk
       
       
    4. The impulse (2mks)
       

       Impulse = mv-mu
       = 200 x 3.85 – 200 x 10
       =200(3.85^-10) √1mk
       =1230Kgm/s

       Impulse = 1230Kgm/s √1mk

19.  
    1. State Boyle’s law. (1mk)
       

       Boyle’s law- States that the pressure of fixed mass of a gas is inversely proportional to its volume, Provided the temperature is kept constant.

    2. Some students carried out an experiment to verify Boyle’s law and their results were as shown in the table below:

       Pressure KN/m2	400	320	160	180
       Volume (m3)	2.0	2.5	5.0	10.0
       1/v (m-3)	0.5	0.4	0.2	0.1

       1. Complete the table (1mk)
       2. Plot a graph of pressure against ¹/_volume (4mks)
    3. Determine the gradient for the graph and state its S.I units (2mks)
    4. A sample of gas has a pressure of 1.0 x 10⁵Pa when its temperature is 10^oC. What will be its pressure when its temperature is raised to 100oC and its volume doubled? (2mks)