Musya
Algebra - Class 8 Mathematics Revision Notes
Algebra
Worked Exercise
- What is the value of x in the equation?
2(3x – 2) = 3x + 8- 12
- 3
- 5
- 4
Working 2 (3x – 2 ) = 3x + 8
Step 1: Open brackets 6x – 4 = 3x + 8
Step 2: Collect like terms and simplify 6x – 3x = 8 + 4 3x = 12 x = 4
The correct answer is D (4)
- Francis has r shillings. John has s shillings. Ouma has sh.150 less than the total money of both Francis and John. Which one of the following expressions gives the total amount of money do the three men have?
- 2r + 2s – 150
- r + s – 150
- 2r + 2s + 300
- r + s + 300
Working
Francis = r
John = s
Ouma = r + s - 150
Total money = r + s + r + s – 150
= 2 r + 2s – 150
The correct answer is A (2r + 2s – 150)
- If x = 2, y = z - x and z = 3, What is the value of
3x – 4y + 2z
2 (x + 2y – z)- 8
- 5
- 7
- 4
Working
Substitute the values of x, y, and z
= (3x2) – (4x1) + (2x3)
2 (2+2 x 1 - 3)
= 8/2 = 4
The correct answer is D (4)
- In a meeting there were 30 women than men and three times as many men as children.If there were 1,360 people altogether. What was the number of children in the meeting?
- 220
- 190
- 600
- 570
Working Men 3x
Children x
Women 3x + 30
Total 7x + 30 = 1360
7x = 1360- 30
7x = 1330
x = 190
Children are 190
The correct answer is B (190)
- What is the value of p in the equation?
¾(8p- 4) = 4p +7- 2
- 5
- 5½
- 2 3/8
Working
¾(8p - 4) = 4p +7
6p – 3 = 4p + 7 (opening brackets)
6p – 4p = 7 + 3 (collecting like terms)
2p = 10
p = 5 (Simplifying)
The correct answer is B (5)
- Omammo is two years older than Temo and three years younger than Mbeti. The sum of their ages is 64 years. If Omamo’s age is m, which of the following equations below can be used to find Omamo’s age?
- 3m + 1 = 64
- 3m – 1 = 64
- 3m – 5 = 64
- 3m + 5 = 64
Working
Omamo = m
Temo = m- 2
Mbeti = m + 3
Total age = 64
X + m – 2 + m + 3 = 64
m + m + m – 2 + 3 = 64
3m + 1 = 64
The correct answer is A (3m + 1 ) = 64
- What is the simplified form of 5x + (8x – 2y)
- 37x – 8y
- 7x –
- 28x – 2y
- 7x – 2y
Working
5x + ¼(8x – 2y ) open brackets
5x + 2x – ½y simplify
= 7x – ½y
The correct answer is B (7x – ½y)
Geometry - Class 8 Mathematics Revision Notes
Geometry
Worked Exercise
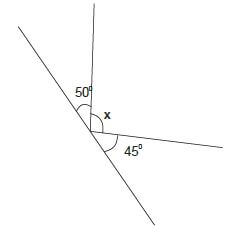
- Find the value of x in the following.
Working
X+45+50=1800 (Angles on a straight lines are supplementary i.e. add up to 180º )
X+95=180º
X=85º
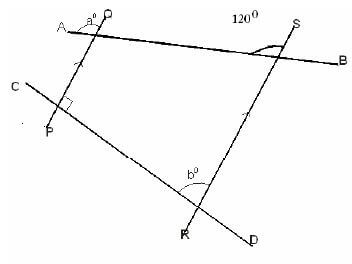
The value of x =85º - Find the sum of angle “a” and angle “b” in the figure below.
Working
Lines AB and C D are transversals are Therefore 90+b = 1800
Co-interior angles - supplementally
Therefore b=180-90
B = 90º
Angle a = 120º - (Corresponding angles)
Therefore a = 120º
Sum of a and b
=120 + 90
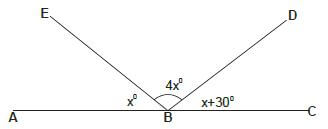
= 210º - Find the size of angle marked A B D in the figure below.
X+4x+x+30=180º (angles on a straight line are supplementary)
= 6x+30=180
6x=180-30
6x = 150
X = 25
Angle A B D =x + 4X
But x = 25
Therefore 25 + (4 x 25)
= 25 + 100
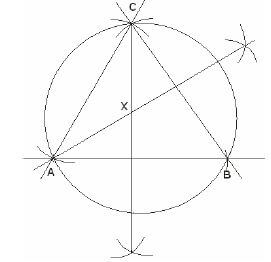
= 125º - Draw an equilateral triangle A B C where Line AB = 6cm.
Draw a circle touching the 3 vertices of the triangle. What is the radius of the circle?
Working
Steps:- Draw line A B = 6cm
- With A as the Centre with the same radius 6cm, mark off an arc above line A B.
- With B as the Centre with the same radius 6cm, mark off an arc above line A B to meet the arc in (II) above. Call the point of intersection point C
- Join C to A and C to B
- Bisect line A B and B C and let the bisectors meet at point X.
- With X as the Centre, draw a circle passing through points A, B and C.
- Measure the radius of the circle.
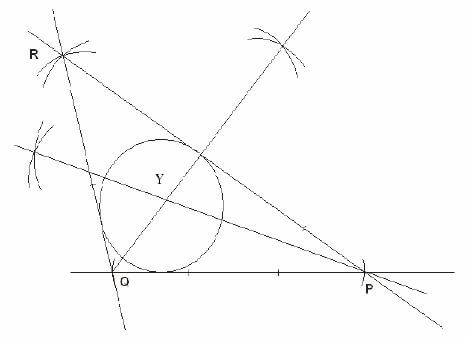
- Construct a triangle P Q R in which Q P = 6cm. Q R = 4cm and P R =8cm. Draw a circle that touches the 3 sides of the triangle, measure the radius of the circle.
Working- Draw line Q P 6cm
- With Centre Q, make an arc 4cm above line Q P.
- With Centre P, make an arc 8cm above line Q P and let the arc meet the one in (II) above. Label the point of intersection as R.
- Join R to P and R to Q.
- Bisect any two angles and let the bisectors meet at point Y.
- With Y as the Centre, draw a circle that touches the 3 sides of the triangle.
Construction
R = 3.5cm
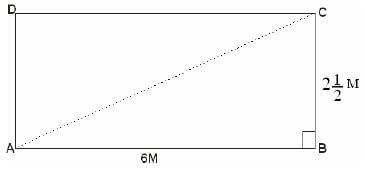
- A rectangle measures 6cm by 2½ cm. What is the length of the diagonal?
Working
AC2 = AB2 + BC2 [ Pythagoras Theorem]
AC2 = 62 + 2 ½2
AC2 = 36 + 6.25
AC2 = 42.25
AC = √42.25
= 6.5 or 6 ½
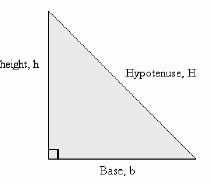
NB: The Pythagoras theorem states
H2 =B2 +h2
h2 = H2 – b2
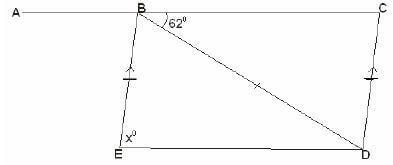
b2 = H2 –h2 - In the figure below, A B C is a straight line and B C D E is a quadrilateral. Angle CBD = 620 and lines EB = BD = DC. Line EB is parallel to DC.
What is the size of angle BDE?
Working
Consider triangle BCD (isosceles triangle)
Therefore base angles are equal
CBD = 62º
BCD = 62º
Therefore, BDC = 180 – 124 = 56º
Angle CDB = angle EBD [Alternate triangle]
Therefore EBD = 56º
Angle BDE =180 - 56/2
= 62º
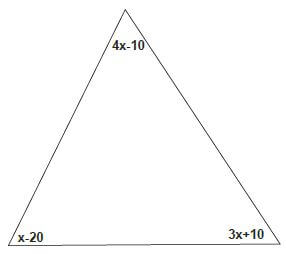
Therefore, BDE = 62º - Find the size of the largest angle from the following triangle.
Working
4X – 10 + x – 20 + 3x + 10 = 180 [Angle sum of a triangle]
8x – 20 = 180
8x = 200
X = 25
4x – 10 = (100 – 10)º
= 90º largest angle.
Time, Speed and Temperature - Class 8 Mathematics Revision Notes
Time, Speed and Temperature
Worked Exercise
- An airplane took 4½ hours to fly from Cairo to Zambia. If it landed in Nairobi at Nairobi at 0215 h on Saturday, when did it take off from Cairo?
- Friday 2145 h
- Saturday 2245h
- Friday 2245h
- Saturday 2145 h
Working
The time the aeroplane took from midnight to 0215h of Saturday = 2h 15min
The difference (4h 30min – 2h 15min) is the time the aero plane took on Friday night.
Time on Friday night
h min
4 30
- 2 15
2 15
= 2h 15min before midnight
Time of takeoff from Cairo
h min
24 00
- 2 15
21 45 on Friday
The correct answer is A (Friday 2145 h)
- A train let Mombasa on Monday at 2125 h and took sixteen and half hours to reach
Kisauni. When did the train reach Kisumu?- Tuesday 1.55 a.m
- Tuesday 1.55 p.m
- Wednesday 1.55 p.m
- Monday 1:55 a.m
Working
Monday: from 2125h to midnight = 2400h - 2125h
= 2h 35min
Tuesday: Number of hours traveled from midnight
= 16h 30min - 2h 35 min
= 13h 55min
The train arrived at Kisumu on Tuesday at 1355h
This is the same as 1.55p.m
The correct answer is B (Tuesday 1.55pm)
- A meeting started at quarter to noon. If the meeting lasted for 2 h 35min, what time in 24-h clock system did the meeting end?
- 1320h
- 1420h
- 1310h
- 1410h
Working
The meeting started at 11.45
Add the meeting time
h min
11 45
+ 2 35
14 20
The meeting ended at 1420h
The correct answer is B (1420 h)
- A wall clock gains 3 seconds every one hour. The clock was set correct at 1pm on Tuesday. What time was it showing at 1pm on Friday on the following week?
Working
The number of days from Tuesday 1 pm to Friday 1pm the following week = 10days.
Number of hours = (24 x 10) = 240 hrs.
The clock gains 3 seconds after every hour in ten days.
240 x 3 = 720 seconds
Min = 720/60 = 12 min
Hence it will show 1 p.m. + 12 min = 1.12 pm
In 24 h clock system
= 1312h
The correct answer is B (1312h) - A cyclist traveled from Nairobi to Nyeri for 4h 30min at a speed of 80km/h. He drove back to Nairobi taking 4 hours. What is his speed, in km/h?
- 90
- 72
- 80
- 100
Working
Distance = speed x time
= 80 x 4½
= 360 km
From Nyeri - Nairobi distance = 360km
Time taken = 4hrs
Therefore speed = Distance/Time
= 90km/h
The correct answer is A (90km/hr)
- A motorist crosses a bridge at a speed of 25m/s. What is his speed in km/hr?
- 80
- 90
- 60
- 30
Working
When working out this kind of question we use a relationship,
If 10 m/s = 36 km/h
25m/s = ?
= ( x 36) km/h
= 90 km/h
The correct answer is B (90km/h)
- The distance between Mombasa and Mtito Andei is 290km. A bus left Mombasa at 1035h and traveled to Mtito Andei at a speed of 50km/h. At what time did it arrive at Mtito Andei?
- 1623h
- 1523h
- 1423h
- 1723h
Working
Time = Distance/Speed
= 290/50
= 5 4/5hours or 5h 48min
Arrival time = Departure time = Time taken + Time taken
h min
10 35
+5 48
16 23
The arrival time 1623 h
The correct answer is A (1623h)
- Kamau drove from town M to town N a distance of 150 km. He started at 9.30 am and arrived at town N at 11.00 am. He stayed in town for one hour and 50 minutes. He drove back reaching town M at 2.30pm. Calculate Kamau’s average speed for the whole journey.
- 90km/h
- 100km/h
- 60km/h
- 150 km/h
Working
Total distance from M to N and back
= 150 x 2
= 300 km
Total time taken
From 9.30 - 11.00 = 1 h 30 min
Time spent in town
= 1 h 50 min
Time taken from N to M
= 1430h – 1250h
= 1h 40min
Total time = 5 hours
Average speed = Total distance/Total time taken
=(60km/h)
The correct answer is C (60km/h)
- The temperature of an object was 20º C below the freezing point. It was warmed until there was a rise of 40º in temperature. What is the reading in the thermometer?
- 60 Cº
- 40Cº
- 20Cº
- 20Cº
Working
Below freezing point means; - 20
Rose by 40º
Therefore - 20º + 40 = 20 C
The correct answer is C (20º C)
Money - Class 8 Mathematics Revision Notes
Money
Worked Exercise
- Mutiso paid sh.330 for an item after the shopkeeper gave him a 12% discount. What was the marked price of the radio?
- sh300
- sh369.60
- sh375
- sh350
Working
Marked price = 100%
Discount = 12%
S.P = 100% - 12%
= 88%
If 88 % = 330
100% = ?
100 x 300/88 = Sh375
The correct answer is C (375)
- Olang’ borrowed sh.54000 from a bank which charged interest at the rate of 18% p.a. He repaid the whole loan after 8 months .How much did he pay back?
- sh6480
- sh60, 480
- sh14580
- sh77760
Working
I = PRT/100
= 54000 x 18 x 8/100 x 12
= sh6480
Amount = P + I
= (54,000 + 6,480) shillings
= Ksh 60, 480
The correct answer is B
- The cash price of a microwave is sh. 18000. The hire purchase price of the microwave is 20% more than the cash price. Bernice bought it on hire purchase terms by paying 40% of the hire purchase price as the deposit and the balance equal monthly installments of sh1620. How many installments did she pay?
- 12
- 10
- 9
- 8
Working
Let the cash price be 100%
Hire purchase = 100% + 20%
= 120% of the cash price
= 120/100 x 1800
= sh.21, 600
Deposit = 40% of HPP
= 40/100 x 21,600
= sh.8, 640
HPP = D + MI
I = HPP - D/MI
= 21600 – 8640/1620 - = 8 Months
The correct answer is D (8)
- Salim deposited sh25000 in a bank which paid compound interest at the rate of 10% per annum. If he withdraws all his money after years, how much interest did his money gain?
- sh5250
- sh2500
- sh1375
- sh387
Working
Interest for year 1
I = PRT/100
= 25000 x 10 x 1/100
= Sh2500
Amount = 25000 + 2500
= 27,500
Interest for 2nd year
I = PRT/100
= 27,500 x 10 x ½/100
= Sh13775
Total interest (2,500 + 1,375)
= Sh3875
The correct answer is D (Sh 3875)
- Kamaru bought bananas in groups of 20 at sh20 per group. He grouped them into smaller groups of 5 bananas each and sold them at sh10 per group. What percentage profit did he make?
- 40%
- 50%
- 60 %
- 70%
Working
For every 20 bananas = sh 25
One group produces 4 smaller groups of 5 bananas each
S. P = 4x 10
= sh40
B.P price = sh25
Profit = 40 – 25
= sh15
% profit = P/BP x 100
= 60%
The correct answer is C (60).
- A shopkeeper bought 3 trays of eggs at sh 150 per tray. On the way to the shop, he realized 20% of the eggs were broken. He sold the rest at sh 72 per dozen. How much loss did he make?
- sh450
- sh432
- sh18
- sh28
Working
B.P for 3 trays = 3 x 150
= sh450
Number of eggs = 3 x 30
= 90 eggs
20% eggs broke = 20/100 x 90
= 18 eggs broken
Therefore remained = (90 - 18) eggs
= 72 eggs
1 dozen = 12 eggs
? = 72 eggs
= 6 dozens
1 dozen = sh.72
6 dozens = ?
Loss = B.P – S.P
= 450 - 432
sh18
The correct answer is C (sh18)
- A Salesperson earns a basic salary of sh7500 per month. He is also paid a 5% commission on all sales above sh30, 000. In a certain month his total earnings were sh.14250. What was his total sales for that month?
- sh135000
- sh285000
- sh165000
- sh315000
Working
Commission = sh14250 – sh7500
= sh6750
5% = sh6750
100% = ?
= 100/5 x 6750
= Sh. 135,000
Total sales = (135,000 + 30,000)
= sh165000
The correct answer is C (sh 165,000)
- Shiku bought the following items from a shop
6kg of sugar @ sh45
½ of tea for sh90
3 kg of rice @ sh30
2kg of fat @ sh70
If she used one thousand shillings to pay for the items, what balance did she receive- sh410
- sh455
- sh590
- sh765
Working
Shiku’s Bill
Total expenditure = sh590Item Sh ct 6kg sugar @ sh45 270 00 ½ kg tea for sh90 90 00 3kg rice @ sh30 90
00 2kg fat @ sh70 140 00 Total 590 00
Balance = sh1000 – sh590
The correct answer is = sh410 (A)
- Maranga paid sh4, 400 for a bicycle after he was given a 12% discount. James bought the same item from a different shop and was given a 15%. How much more than James did Maranga pay for the bicycle?
- sh250
- sh300
- sh750
- sh150
Working
Maranga B.P = 100% - 12%
= 88%
4400/88 x 100 = sh5000
James B.P = 100% - 15%
= 85%
85 x 100/4400 = sh4,250
How much more? = (5000-4250) shillings
= sh750
The correct answer is C (750)
- The table below shows postal charges for sending letters;
Mass of letter Sh ct Up to 20g 25 00 Over 20g up to 50g 30 00 Over 50g up to 100g 35 00 Over 100g up to 250g 50 00 Over 250g up to 500g 85 00 Over 500g up to 1kg 135 00 Over 1kg up to 2kg 190 00
Namu posted two letters each weighing 95g and another one weighing 450g. How much did he pay at the post office?- sh120
- sh135
- sh155
- sh240
Working
Two letters
95g → Sh35.00
95g → Sh35 .00
Another 450g → Sh85.00
The correct answer is C (sh155)
Volume, Capacity and Mass - Class 8 Mathematics Revision Notes
Volume, Capacity and Mass
Worked Exercises
- A Jerry can contains 5 litres of juice. This juice is used to fill 3 containers each of radius 7 cm and height of 10cm. How many milliliters of juice are left in the jerry can?
- 38
- 480
- 400
- 420
Working
Volume of container: = Πr2 h
=22/7 x 7 x 7 x 10
= 1540 cm3
Volume of 3 such containers
= (1540x3) cm3
= 4620 cm3
Volume of juice in jerry can = (5 x 1000)
= 5000cm3
Volume of juice left = (5000-4620) cm3
= 380 cm3
= 380 ml
The correct answer is A (380ml)
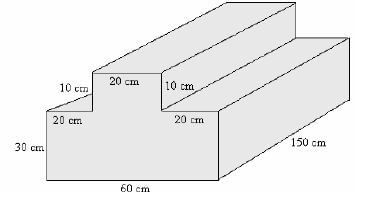
- The diagram below represents a solid whose dimensions are shown.
What is the volume in cm3?- .30000
- 300000
- 3000
- 3000000
Working
Volume = Area of the Cross-section x length
Volume of the top = (20 x 10 x 150)
= 30,000cm3
Volume of the bottom = 60 x 30 x150
= 270,000cm3
Whole solid = top + bottom
= 30,000 + 270,000
= 300,000cm3
The correct answer is B (300 000)
- In the month of October, a farmer delivered 48750kg of maize to a miller. In November the amount of maize delivered was 1850kg more than that of October. The amount delivered in December was 2450kg less than that of November. What was the total mass, in tonnes, was delivered by the farmer in the 3 months?
- 145.65
- 147.5
- 152.4
- 150.55
Working
October = 48750 kg
November = (48750+1850) kg
= 50,600 kg
December = 50,600-2,450) kg
= 48,150 kg
Total mass = 48750+50600 +48150
= (147500/1000) tonnes
= 147.5 tonnes.
The correct answer is B (147.5)
- A rectangular tank measures 1.2m by 80cm by 50cm. water is poured into the tank to a height of 15cm. How many more liters of water are needed to fill the tank?
- 144
- 14.4
- 33.6
- 336
Working
Capacity of the tank = 120 x 80 x 50
= 480,000cm3
Convert to litres = 480,000/1000
= 480litres
Volume of the water poured = 120 x 80 x 50
= 144000cm3
Convert to litres = 144000/1000
= 144 litres
Volume of water needed = 480 – 144 = 366litres.
The correct answer is D (366)
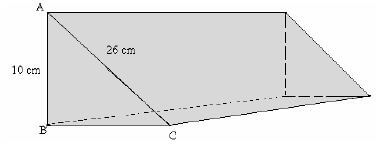
- The diagram below represents a solid triangular prism.
What is the volume in cm3?- 2400
- 2000
- 5200
- 576
Working
Apply Pythagorean relation in triangle ABC
BC =√262 -102
=√576
= 24cm
Volume = Area of the Cross section x length
= ½ x 24 x 10x 20
= 2400cm3
The correct answer is A (2400cm3)
- A cylindrical tank has a radius of 2m and a height of 1.5m. The tank was filled with water to a depth of 0.5M. What is the volume of water in the tank, in litres? (П = 3.14)
- 6280
- 628
- 9240
- 18840
Working
Volume = П r 2h
= 3.14 x 2 x 2 x 0.5
= 6.28 m3
In litres = (6.28 x1000) litres
= 6280 litres
The correct answer A (6280)
- When processed, 7kg of coffee beans produce 1kg of processed coffee. Processed coffee is then packed in 50kg bags. A farmer delivered 5.6 tonnes of coffee berries in one month. How many bags were obtained?
- 12
- 16
- 40
- 20
Working
Mass of coffee berries = 5.6tonnes
= 5.6x1000
= 5600kg
Mass obtained = 5600/7
= 800kg
Number of bags = 800 ÷ 50
= 16 bags
The correct answer is B (16)
- A rectangular container whose base measures 40cm by 60cm has 30 liters of water when full. Find the height of the container in cm.
- 0125
- 1.25
- 12.5
- 125
Working
V = base area x height
Height = volume/base area
Volume = 30 litres
= 30x1000
= 30,000cm3
Height = 30,000/2400
= 12.5cm
The correct answer is C (12.5)
- A shopkeeper had 43 litres sand 5 litres and 5 dl of paraffin. He packed all the paraffin in 7.5 dl-containers. How many containers did he fill?
- 58
- 5.8
- 6
- 60
Working
Convert decilitres into litres
1 dl =1/10 litres
5 dl =5/10 litres
7.5 dl =7.5/10 litres = 0.75 litres
Hence 43 litres 5dl = 43.5 litres
No of containers = 43.5/0.75 = 58 containers
The correct answer is 58 (A)
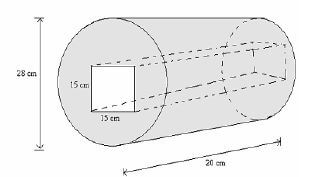
- The figure below shows a cylindrical solid of diameter 28cm and length 20 cm. A square hole of side 1.5 cm has been removed. What is the volume of the material in the solid, in 3cm3?
- 12320
- 4500
- 8400
- 7820
Working
Volume of solid = volume of a cylinder - volume of the square hole
= ( x 14 x 14x 20) - (15 x 15 x 20)
= 12320 - 4500
= 7,820 cm3
The correct answer is D (7,820cm3)
Measurements - Class 8 Mathematics Revision Notes
Length, Perimeter and Area
Worked Exercise
- Tracy used a piece of wire m long to support tomato plants in the garden. The wire was cut into pieces of 28cm long. How many complete pieces were obtained?
- 85
- 30
- 20
- 30.10
Working
1 M = 100cm
8½m = ?
8½ x 100 = 850cm
1 piece = 28 cm
? = 850cm
= 850/28
= 30 complete pieces remainder 10cm
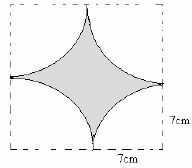
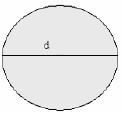
- The figure below represents a flower garden
What is the perimeter of the garden?- 25m
- 38.5m
- 11m
- 44m
Working
P = ¼П d + r + r
= ( ¼ x 22/7 x 14) + (7+7)
= 11 + 14
= 25 m
The correct answer is A (25)
- The parallel sides of a trapezium measure 10cm by 18cm respectively. If the distance between the parallel sides is 8cm, what is the area of the trapezium in cm²?
- 224
- 112
- 108
- 84
Working
Area of a trapezium = ½h (a + b)
= ½ x 8 x (10+18)
= ½ x 8 x 28
= 112cm²
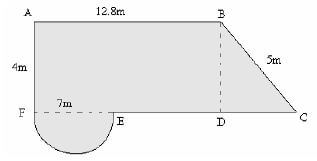
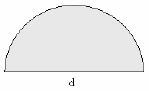
- The figure below shows vegetable garden.
What is the perimeter?- 0.526m
- 5.26m
- 52.6m
- 526m
Working
Perimeter of semi-circle
= ½П d(Circumference only)
=½ x 2 x 22/7 x 7
= 22m
To get DC = √ 25 – √ 16
= √ 9
= 3m
Length DE = AB – ED
= 12.8 – 7
= 5.8m
Total length 12.8+ 5 + 3 + 5.8 + 22 + 4
= 52.6 m
The correct answer is (52.6)
- What is the perimeter of the following shape?
- 88cm
- 44cm
- 176cm
- 56cm
Working
P = circumference of a circle of radius 7cm
= 2Π r
= 2 x 22/7 x 7
= (44 cm)
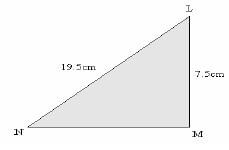
- The figure below shows a right angled triangle LMN in which LM = 7.5cm and LN = 19.5cm
What is the area of the triangle in cm²?- 18
- 67.5
- 27
- 34.5
Working
Apply Pythagoras relation in triangle LMN
LN² = LM² + NM²
Nm² = LN² – LN²
= 19.5² – 7.5²
= 380.25 – 56.25
= 324
NM = √ 324
= 18 cm
Area of triangle LMN
= Base x height
= ½ X 18 X 7.5
= 67.5cm²
The correct answer is B (67.5cm²)
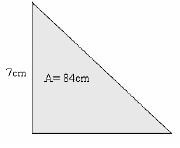
- The area of a right-angled triangle is 84cm². If the height of the triangle is 7cm, what is the length of the longest side?
- 25cm
- 24cm
- 19cm
- 12cm
Working
The Pythagoras relationship states that
H² = b² + h²
But Area = ½bh
84 =½ x b x 7
84 x 2 = 7b
24 = b
H² = 24² + 7²
H² = 576 + 49
H² = 625
H = 25
Therefore the correct answer is 25cm (A)
- What is the surface area of an open cylinder whose radius is 6.3cm and height of 25cm.
- 114.74cm²
- 1239.48cm²
- 3118.50cm²
- 619cm²
Working
Total surface area = Πr2+Πdh
= ( 22/7x 6.3 x 6.3) + 2 x 22/7 x 6.3 x 25
= 124.74 + 990
= 1114.74 cm²
The correct answer is 1114.74 cm² (A)
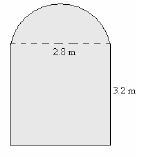
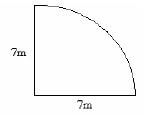
- A Welder made a door with a design as shown below.
What is its area? (Take Π =22/7 )- 15.12m²
- 12.04m²
- 13.36m²
- 21.28m²
Working
Area of the semi- circle = ½Π r²
= ½ x 22/7 x 1.4 x 1.4
= 3.08m²
Area of the rectangle = L x w
= 3.2 x 2.8
= 8.96 m²
Total area = (3.08 + 8.96 )m²
= 12.04 m²
The correct answer is B (12.04m²)
- The diagram below represents a plot with a diameter of 28 meters.
The plot was fenced by erecting posts 4m apart. How many posts were used ? (Π = 22/7)- 12
- 17
- 18
- 19
Working
Perimeter =½ П d + d
= (½ x 22/7 x 28 + 28)
= 72
No of posts = Perimeter/Interval
=72/4
= 18 posts
The correct answer is C (18)
Numbers - Class 8 Mathematics Revision Notes
In this section you will need the following hints to solve the exercises:
- Place value of whole numbers
- Total value of whole numbers
- Multiplication of whole numbers/tables
- BODMAS
- LCM and GCD
Worked Exercise
- What is four million seventy thousand and five hundred and thirty three?
- 4,070,353
- 4,070,533
- 4,007,533
- 4,700,533
Working
Using the place value table, the question can be solved as follows:
The correct answer is B (4070533)
MillionsHundred
ThousandsTen
thousands
Thousands
Hundreds
tens
Ones4 0 7 0 5 3 3
- What is the square root of 7 9/16
- 7 ¾
- 2 ¾
- 1 3/8
- 21/16
Working
Step 1: Change the mixed fraction to improper Find the square root of both numerator and denominator.
Step 2: Find the square root of both numerator and denominator
= √121
√16
=11/4
Step 3: Change the improper fraction to mixed fraction
= 2¾
The correct answer is B
- What is 25% as a fraction?
- 1/5
- ¾
- ½
- ¼
Working
Step1: Express the percentage with 100 as a denominator.
=25/100
Step 2: Simplify
=¼ correct answer is D
- What is the value of of 1/3 of(½ + 1/9) ÷1/6
- 11/324
- 1/99
- 12/9
- 4/11
Working
Step1: Using the order of operation, BODMAS, solve the brackets first.
1/2 + 1/9 = 11/18
Step 2: Open brackets and calculate ‘of ‘
=1/3 of (11/18) ÷ 1/6
=1/3 x (11/18) ÷ 1/6
=11/54 ÷ 1/6
Step3: Calculate the division part
=11/54 ÷ 1/6
=11/54 x 6/1(multiply by the reciprocal of 1/6)
=11/9
Step 4: Change the improper fraction to mixed fraction.
= 1 2/9
The correct answer is C.
- The price of radio is Sh1800. The price was reduced by 15% during an auction. How much is the price after the reduction?
- Sh270
- Sh2070
- sh1530
- sh1785
Working
Marked price = Sh1800
Percentage decrease = 15%
New price
85% of Sh1800 (100% - 15%)
= 85 x 1800/100
= Sh1, 530
The correct answer is Sh 1530 (C)
- In a certain year a tea factory produced 2500 tonnes of tea leaves. The following year the tonnes increased to 4000. What is the percentage increase?
- 160%
- 62½ %
- 60%
- 37½ %
Working
First year = 2500 tonnes
Second year = 4000 tonnes
Increase = 1500 tonnes (4000-2500)
% Increase = Increase x 100/Original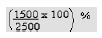
= 60%
The correct answer is C (60%)
- What is the next number in the sequence below.
6, 10, 19, 35, ….. - 60
- 84
- 71
- 51
Working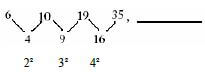
The next difference is 5² = 25
The next number is 35 + 25 = 60
The correct answer is A (60)
Properties of Geometric Shapes - Class 8 Mathematics Revision Notes
General Geometric Shapes
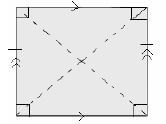
Square
- All sides are equal
- Opposite sides are parallel
- Each interior angle is a right angle (90º)
- The interior angles total up to 360º
- Diagonals bisect each other at right angles.
- Diagonals measure the same length and bisect interior angles.
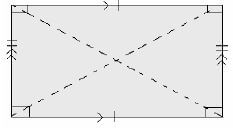
Rectangle
- Each interior angle is 90º and they all add up to 360º
- Diagonals are equal
- Diagonals bisect each other but NOT at right angles
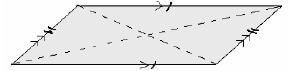
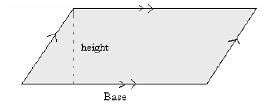
Parallelogram
- Opposite sides are equal and parallel
- Opposite angles are equal
- Diagonals bisect each other
- Diagonals are not equal
- Adjacent angles are supplementary (add up to 180º)
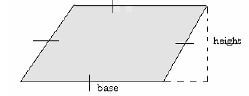
Rhombus
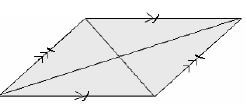
- All sides are equal
- Opposite sides are parallel
- Opposite angles are equal
- Diagonals bisect each other at 90º
- Diagonals bisect the interior angles
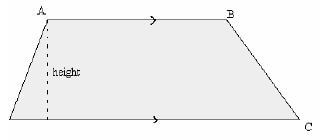
Trapezium
- The sum of the interior angles is 360º
- Has a pair of parallel lines which are not of the same length
- Has a perpendicular height joining the two parallel lines
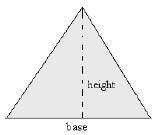
Right-angled Triangle (Pythagorean relationship)
- H2 = b2 + h2
- b2 = H2 – h2
- H2 = H2 - b2
Examples of relationships
Base Height Hypotenuse 3 4 5 6 8 10 5 12 13 7 24 25 8 15 17 9 40 41
Properties of Triangles and Parallel Lines
Triangle
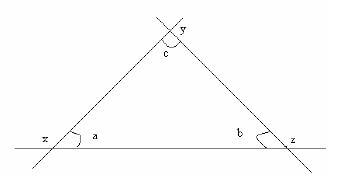
Exterior angles & interior angles
- Angles x, y, and z are exterior angles while a, b, and c are interior angles.
- Exterior angles add up to 360º while interior angles add up to 180º.
- Angles x, a; b, z; and c, y; are adjacent to each other and they add up to 180º (supplementary angles)
Parallel Lines and Transversal
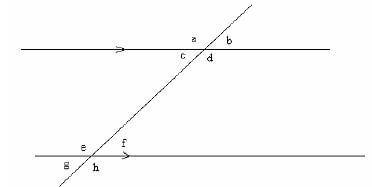
- Angles at a point e.g. a + b+ c + d = 360º
- Vertically opposite e.g. a/d, b/c, f/g, e/h. They are equal
- Corresponding angles e.g. b/f, a/e, c/g, d/h. They are equal
- Alternate angles e.g. c/f, d/e are always equal.
- Co-interior angles e.g. c/e, d/f, are always equal.
- Co-interior/allied angles e.g. c/e, d/f are formed by parallel lines. They are supplementary.
Speed, Distance and Time
The formulae related to speed, distance and time can be derived from the following triangle.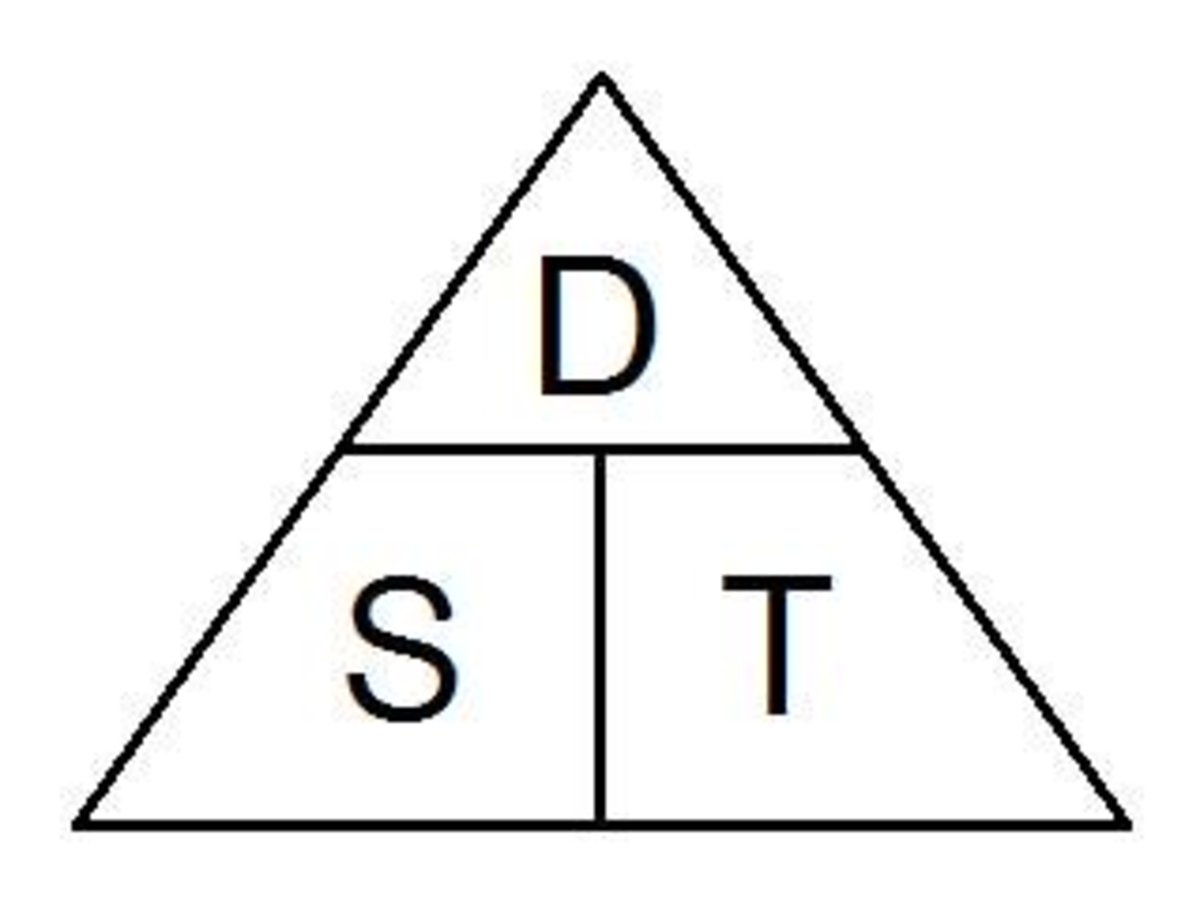
General Mathematics Formulae - Class 8 Mathematics Revision Notes
- Length
- Mass
- Volume And Capacity
- Time
- Area
- Surface Area
- Volume of Cylinder and Rectangular Shapes
- Perimeter
- Expressing areas of Large Shapes
Length
The units of length that are used include the following:
- millimetre (mm)
- centimetre (cm)
- decimetre (dm)
- Metre (m)
- Dekametre (Dm)
- Hectometre (Hm)
- Kilometre (Km)
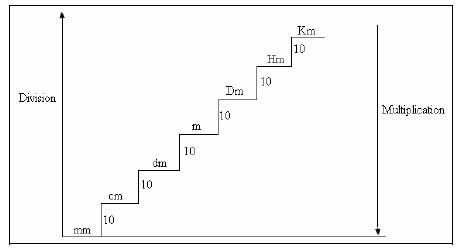
From the illustration:
- 10mm = 1cm
- 10cm = 1dm
- 10dm = 1m
- 10m = 1 Dm
- 10Dm = 1Hm
- 10 Hm = 1Km
The relationship between the units of lengths may be clearly seen if the units are written with a 10 between them.
So to find how many small units are equivalent to another, multiply the number of tens between the units, hence:
- Km 1
- Hm 10
- Dm 100
- M 1000
- dm 10000
- mm 1000000
Mass
- 1000 g = 1Kg
- 1000 Kg = 1Tonne
- 1000000 g = 1Tonne
Volume and Capacity
- 1 cm3 = 1 Ml (millilitre)
- 1000 cm3 = 1 L (litre)
- 100 cm3 = 1 dl (decilitre)
- 1 m3 = 1000 litre
- 1000000 cm3 = 1 m3
- 10 dl = 1 Litre
- 1000ml = 1 Litre
Time
- 60 Seconds = 1 Minute
- 60 Minutes = 1Hour
- 3600 Seconds = 1 Hour
- 24 Hours = 1 day
- 7 Days = 1 Week
Area
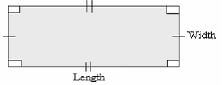
Rectangle
Area = Length x Width
A = L X W
Square
Area = Side x Side
A = S x S
A = S2
Parallelogram
A = base x Height
A = b x h
Rhombus
Area = base x height
A = b x h
Triangle
Area = base x height
A = b x h
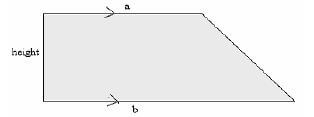
Trapezium
Area = x sum of parallel lines x height
A = (a + b) x h
A = h (a + b)
Circle, half circle, quarter circle
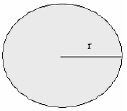
Circle
Area = П x radius x radius
A = П x r x r
A = Пr2
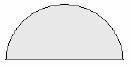
Half circle
Area = Area of a full circle ÷ 2
A = П r2
2
A =½ Пr2
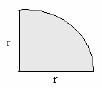
Quarter circle
A = Area of the full circle ÷ 4
A = Пr2 ÷ 4
A = ¼Пr2
Note: П = 22/7 or 3.14 or 3 1/7
Surface Area
Surface Area of a Cylinder
T.S.A = Area of circular ends + area of the curved surface
=2Пr2 + Пdh ( if closed both ends)
T.S.A = Пr2 + Пdh (if open one end )
T.S.A = Пdh (if open both ends/pipe)
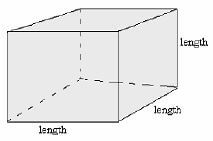
Surface Area of a Cube
T.S.A = Total area of all the six faces
= 6 x L x L
= 6L2 (if closed)
or
= 5L2 (if open one end)
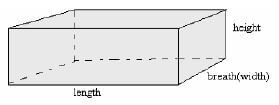
Surface Area of a Cuboid
T.S.A = Total area for the six faces
= 2 (L x w) + 2 (L x h) + 2 (w x h)
or
= (L x w) + 2 (L x h) + 2(w x h) ( if open on top)
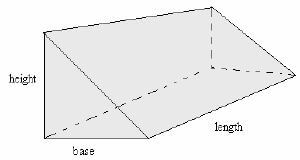
Surface Area of a Triangular prism
T.S.A = Area of all the 5 faces of the prism
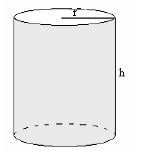
Volume of Cylinder and Rectangular Shapes
Volume of a Cylinder
Volume = Base area x height
= Пr2 x height
= Пr2h
Volume of a Rectangular shape
Volume = Base area x height
V = L x w x h
Note: Depending on the cross-section, the volume of any shape / solid is given by.
V = Area of cross-section x height/length
Perimeter
Perimeter of a Rectangle
P = Length + Length + Width + Width
= L + L + W + W
= 2L + 2W or 2(L + W)
Perimeter of a Square
P = L + L + L + L
= 4L
Perimeter of a Circle
C = П x diameter
= Пd or 2Пr
Note: Perimeter of a full circle is called circumference
Perimeter of a Half a Circle
Perimeter = circumference + diameter
P = ½Пd + d
Note: For triangles and irregular shapes, JUST ADD THE DISTANCE ALL ROUND.
Expressing area of large shape
Hectare – A shape that measures 100m by 100m
Therefore 1ha = (100 x 100)m2
1 ha = 10000m2
Are – a piece / shape that measures 10m by 10m
Therefore 1 are = 10 x 10
1 are = 100m2
Hence:
1 ha = 10000m21are = 100m2
1ha = 100ares
Social Relations And Cultural Activities - Class 8 Social Studies Revision Notes
The School
- A school is a centre where learning takes place both formally and informally.
- It is also a place where the learners acquire knowledge.
School Management
- The public schools are run by the government through the ministry of education.
- At the district level, the schools are managed by:
- the District Education Board. (D.E.B)
- The chairman of the district education board is the district commissioner.
- The secretary of the District education board is the district education officer (D.E.O)The D.E.O is in charge of all the education matters in the district. He/She:-
- Ensures there are teachers in the school.
- Inspects schools to ensure standards are set and maintained.
- Organizes co-curriculum activities.
- Assigns teachers responsibilities by posting and transferring them.
The Teacher
- He/She is the secretary to the school committee.
- He/She signs duties and responsibilities to all the teachers in the school
- Receive information from the ministry and pass them on to teachers.
- Ensures that the school is stable and runs smoothly.
- He supervises the work of teachers, pupils and school workers.
- He ensures that good academic standards are made and maintained.
- He writes minutes during school committee meetings.
- He maintains discipline among pupils.
The Deputy Headteacher
- He is the principal assistant of the head teacher.
- He attends to lessons by planning and teaching.
- He acts in the absence of head teacher.
- He is in charge of discipline.
The Senior Teacher
- Ensures all lessons are attended to.
- Acts in the absence of head teacher and the Deputy head teacher.
- Plans and teaches the pupils.
Head Prefects (head boy and head girl)
- They co-ordinate the activities of other prefects.
- Ensures the pupils are orderly.
- Prefects act as the eyes of teachers on other pupils.
Importance of School Administration.
- It promotes high academic standards.
- It promotes high standards of discipline.
- It helps in maintaining school facilities like chairs tables and desks.
- It co-ordinates the daily academic activities in the school.
- It maintains proper school records.
- It organizes and promotes co-curricular activities in the schools e.g. games, music, athletics, drama.
- It acts as the link between the community in school.
- It ensures that the school maintains cleanliness.
- It acts as a link between the school and the government education agents like:
- Assistant education officers (AEO)
- District Education Officers
- Provincial director of education
- It allocates teachers their teaching subjects and other duties.
The School Motto
- It is a phrase that expresses the beliefs of a school.
- It describes the goals that a school intends the school learners to achieve by the time they leave the school.
- School routine is the program of activities in the school either on daily or weekly basis.
- The school timetable forms a major part of the school routine.
The Family
- Family is a group of people who are related by blood or marriage.
Main Types of Family
- Nuclear family - father, mother and child/children
- Extended family - nuclear and other relatives.
- Single parent family - One parent and child/children
Needs of Family Members
- Needs are requirements that are necessary for people to live.
- Basic needs - things we cannot do without.
- Secondary needs - Things that add comfort to our lives but we can do without them.
| Basic needs | Secondary needs |
|
|
Resonsibilities of Family Members
- Roles and duties in a family are well defined.
EXAMPLES:
Responsibilities of Parents
- Providing basic needs for the family.
- Providing security in the family.
- Providing medical care for the family.
- Installing good morals in the children.
- Providing financial assistance.
- Teaching religious values.
- Providing love for the family members.
Marriage
- Marriage is a permanent union between adults.
- Marriage systems recognized in Kenya are:
- Religious marriage.
- Customary marriage.
- Civil marriage.
Religious Marriage
- It is usually conducted in a church , mosque , or a temple.
- A wedding ceremony is conducted.
- Christians and Asian marriages are monogamous (one man and one wife)while Muslim marriages are polygamous (more than one wife).
- Couple exchange marriage vows.
- A marriage certificate is issued.
Customary Marriage
- Conducted according to the African customs and beliefs.
- Polygamy is allowed.
- Bride wealth is given before the wedding ceremony.
- It is usually conducted by the clan elders.
Civil Marriage
- It is presided over by a magistrate or an authorized government officer.
- A couple intending to marry must issue a 21 day notice to the district commissioner or the district registrar of marriage.
- The marriage partners pay a marriage fee.
- A marriage certificate is issued.
- Divorce or separation is granted by a court of law.
Importance of Marriage
- It provides companionship.
- It ensures the continuity of the family name and culture.
- It unites different families hence promotes unity and harmony in the society.
- It ensures good upbringing of the children.
- It provides security and legal rights to the children, wife, and the husband.
- It helps to regulate social behavior of the couple.
- It helps to enrich culture especially when man and wife are responsible.
Rights and Responsibilities of Spouses in Marriage
- To be loyal and faithful to each other.
- To stand by each other as a source of comfort and strength.
- To love one another.
- To give each other emotional and physical security and protection.
- To earn an income to support the family.
- To promote the family’s standard of living.
- To discuss the decisions regarding the family matters.
- They should be caring to the children.
Succession and Inheritance
- Succession means taking over property after the owner dies or give up ownership.
- Inheritance is receiving property left behind when the owner dies.
- People succeed or inherit the estate (belonging of the deceased ) through:
- customary laws
- written wills
- parliamentary acts (law of succession).
- The property of the diseased is called an estate.
- A written document that shows how the property of the deceased should be shared out is known as the will.
- The person who inherits the estates of the deceased is known as an heir.
- The distribution of the estate of the deceased is done by:
- Court of law.
- The public trustee.
- The bearer of the letter of administration or the grant of probate.
- The authority to manage the estate is granted by a court of law.
- The following are entitled to the estate of the deceased :
- wife or wives
- former wife ( in case of a divorce in a court of law).
- sons
- daughters
- parents
- Any other person with proof that they depend on the deceased.
- Where both the parents have died, the adult first born child should apply to get a letter of administration, if the parent did not leave a will or a grant of probate, if the parent left a will.
NB: daughters of the deceased whether married or not have the right to benefit from the property of the deceased.
Resources and Economic Activities.
- Resources are the things that are useful to human beings e.g. Soil, water, money, land, forest, mineral, wildlife, domestic animals.
- Economic activities are the different ways that we use the resources to earn income.
- The main economic activities in Kenya include:
- Transport and communication.
- Livestock keeping.
- Wildlife and tourism.
- Fishing.
- Mining.
- Crop farming.
- Forestry.
- Manufacturing.