Scale Drawing - Mathematics Form 1 Notes

The Scale

The ratio of the distance on a map to the actual distance on the ground is called the scale of the map. The ratio can be in statement form e.g. 50 cm represents 50,000 cm or as a representative fraction (R.F), 1 : 5,000,000 is written as ¹/_5,000,000

Example

The scale of a map is given in a statement as 1 cm represents 4 km. convert this to a representative fraction (R.F).

Solution

One cm represents 4 x 1 00,000 cm. 1 cm represents 400, 000
Therefore, the ratio is 1 : 400,000 and the R.F is ¹/_400,000

Example

The scale of a map is given as 1:250,000.Write this as a statement.

Solution

1 :250,000 means 1 cm on the map represents 250,000 cm on the ground. Therefore, 1 cm represents ^250,000/_100,000 km
I.e. 1 cm represents 2.5 km.

Scale Diagram

When during using scale, one should be careful in choosing the right scale, so that the drawing fits on the paper without much details being left.

Bearing and Distances

Direction is always found using a compass point.
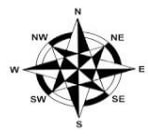
A compass has eight points as show above. The four main points of the compass are North, South, East, and West. The other points are secondary points and they include North East (NE), South East (SE), South West (SW) and North West (NW).Each angle formed at the centre of the compass is 45⁰the angle between N and E is 90⁰.

Compass Bearing

When the direction of a place from another is given in degrees and in terms of four main points of a compass. E.g. N45 0 W, then the direction is said to be given in compass bearing.
Compass bearing is measured either clockwise or anticlockwise from North or south and the angle is acute.

True Bearing

North East direction, written as N450 E can be given in three figures as 045⁰measured clockwise from True North.
This three- figure bearing is called the true bearing.
The true bearings due north is given as 000⁰.Due south East as 135⁰and due North West as 315⁰.

Example

From town P, a town Q is 60km away on a bearing South 80º east. A third town R is 100km from P on the bearing South 40º west. A cyclist travelling at 20km/h leaves P for Q. He stays at Q for one hour and then continues to R. He stays at R for 1½ hrs. and then returns directly to P.

Calculate the distance of Q from R.

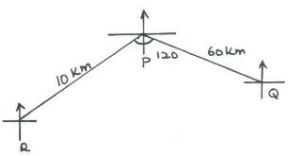
P² = 100² + 60² - 2(100) (60) Cos 120
P² = 13600 – 12000 Cos 120
P² = 19600
P = 140km
Calculate the bearing of R from Q.
140 = 100
Sin 120 Sin Q
= 38.2°
Bearing 270 – 38.2 = 241.8°
What is the time taken for the whole round trip?
Time from P to R = ⁶⁰/₂₀ = 3 hrs
Time from Q to R = ¹⁴⁰/₂₀ = 7 hrs
From R to P = ¹⁰⁰/₂₀ = 5 hrs
Taken travelling = 3 + 7 + 5
= 15hrs

Example

A port B is on a bearing 080^o from a port A and a distance of 95 km. A Submarine is stationed at a port D, which is on a bearing of 200^ofrom A, and a distance of 124 km from B. A ship leaves B and moves directly Southwards to an Island P, which is on a bearing of 140^ofrom A. The Submarine at D on realizing that the ship was heading to the Island P, decides to head straight for the Island to intercept the ship.

Using a scale of 1 cm to represent 10 km, make a scale drawing showing the relative positions of A, B, D and P. {4 marks}

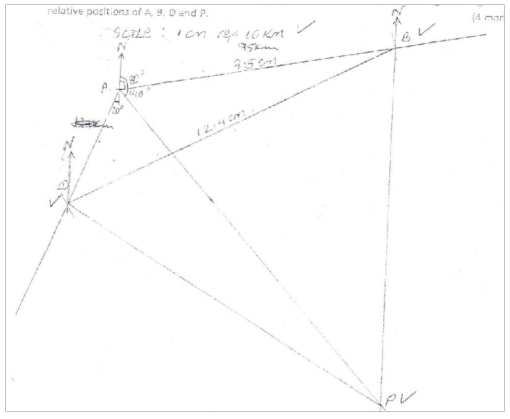
B₁ for all three correct
Hence find:
1. The distance from A to D.
  4.6 ± 0.1 ×10 = 46 KM ± 1 Km
2. The bearing of the Submarine from the ship when the ship was setting off from B
  240° ± 1° OR S 60 ° W ± 2°
3. The bearing of the Island P from D.
  122° ± OR S 58° E ± 1°
4. The distance the Submarine had to cover to reach the Island P
  127 ± 0.1 ×10 = 127 ± 1 Km

Angle of Elevation and Depression

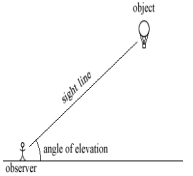
Angle of Elevation:

angle of elevation

The angle above the horizontal that an observer must look to see an object that is higher than the observer. Example, a man looking at a bird.

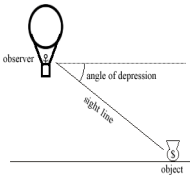
Angle of Depression:

angle of depression

The angle below horizontal that an observer must look to see an object that is lower than the observer. Example, a bird looking down at a bug.
Angles of depression and elevation can be measured using an instrument called clinometer
To find the heights or the lengths we can use scale drawing.

Simple Survey Methods

This involves taking field measurements of the area so that a map of the area can be drawn to scale. Pieces of land are usually surveyed in order to:
- Fix boundaries
- For town planning
- Road construction
- Water supplies
- Mineral development

Areas of Irregular Shapes

Areas of irregular shape can be found by subdividing them into convenient geometrical shapes e.g. triangles, rectangles or trapezia.

Example

The area in hectares of the field can be found by the help of a base line and offsets as shown.
XY is the base line 360m. SM,RP and QN are the offsets.
Taking X as the starting point of the survey,the information can be entred in a field book as follows.
offsets and baseline
The sketch is as follows:
Using a suitable scale.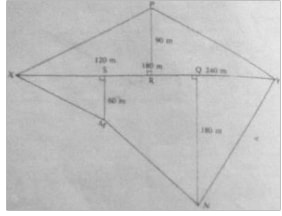
scale drawing irregular shape
The area of the separate parts is found then combined.
Area of:
Triangle XPR is ½ x1 80 x 90 = 8100 m²
Triangle PRY is ½ x1 80 x 90 = 8100 m²
Triangle XSM is ½ x1 20 x 60 = 3600 m²
Triangle QNY is ½ x1 20 x 1 80 = 10800m²
Trapezium SQNM = ½(QN + SM) x SQ m²
½(180 + 60) x 120 m²
= 14400m²
Total area = 8100 + 8100 + 3600 + 10800 + 14400 = 45000m²

Past KCSE Questions on the Topic

A point B is on a bearing of 080⁰from a port A and at a distance of 95 km. A submarine is stationed at a port D, which is on a bearing of 200⁰from AM and a distance of 124 km from B. A ship leaves B and moves directly southwards to an island P, which is on a bearing of 140 from A. The submarine at D on realizing that the ship was heading fro the island P, decides to head straight for the island to intercept the ship. Using a scale of 1 cm to represent 10 km, make a scale drawing showing the relative positions of A, B, D, P. Hence find
1. The distance from A to D
2. The bearing of the submarine from the ship was setting off from B
3. The bearing of the island P from D
4. The distance the submarine had to cover to reach the island P
Four towns R, T, K and G are such that T is 84 km directly to the north R, and K is on a bearing of 295⁰ from R at a distance of 60 km. G is on a bearing of 340⁰from K and a distance of 30 km. Using a scale of 1 cm to represent 10 km, make an accurate scale drawing to show the relative positions of the town.
Find
1. The distance and the bearing of T from K
2. The distance and the bearing G from T
3. The bearing of R from G
Two aeroplanes, S and T leave airports A at the same time. S flies on a bearing of 060 at 750 km/h while T flies on a bearing of 210⁰at 900km/h.
1. Using a suitable scale, draw a diagram to show the positions of the aeroplane after two hours.
2. Use your diagram to determine
  1. The actual distance between the two aeroplanes
  2. The bearing of T from S
  3. The bearing of S from T
A point A is directly below a window. Another point B is 15 m from A and at the same horizontal level. From B angle of elevation of the top of the bottom of the window is 30⁰ and the angle of elevation of the top of the window is 35⁰. Calculate the vertical distance.
1. From A to the bottom of the window
2. From the bottom to top of the window
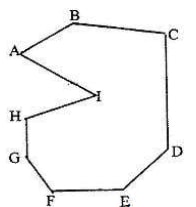
Find by calculation the sum of all the interior angles in the figure ABCDEFGHI below
Shopping centers X, Y and Z are such that Y is 12 km south of X and Z is 15 km from X. Z is on a bearing of 3300 from Y. Find the bearing of Z from X.
An electric pylon is 30m high. A point S on the top of the pylon is vertically above another point R on the ground. Points A and B are on the same horizontal ground as R. Point A due south of the pylon and the angle of elevation of S from A is 26⁰. Point B is due west of the pylon and the angle of elevation of S from B is 32⁰. Find the
1. Distance from A and B
2. Bearing of B from A
The figure below is a polygon in which AB = CD = FA = 12cm BC = EF = 4cm and BAF =- CDE = 120⁰. AD is a line of symmetry.

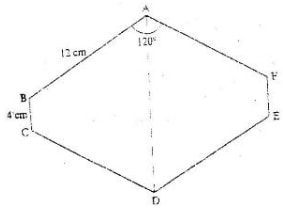
Find the area of the polygon.
The figure below shows a triangle ABC
1. Using a ruler and a pair of compasses, determine a point D on the line BC such that BD:DC = 1:2.
2. Find the area of triangle ABD, given that AB = AC.
A boat at point x is 200 m to the south of point Y. The boat sails X to another point Z. Point Z is 200m on a bearing of 310⁰from X, Y and Z are on the same horizontal plane.
1. Calculate the bearing and the distance of Z from Y
2. W is the point on the path of the boat nearest to Y. Calculate the distance WY
3. A vertical tower stands at point Y. The angle of point X from the top of the tower is 60 calculate the angle of elevation of the top of the tower from W.
The figure below shows a quadrilateral ABCD in which AB = 8 cm, DC = 12 cm, ∠BAD = 45⁰, ∠CBD = 90⁰and ∠BCD = 30⁰.

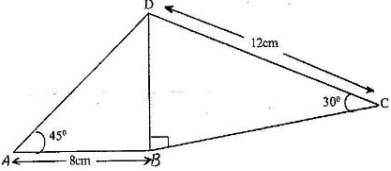
Find:
1. The length of BD
2. The size of the angle ADB
In the figure below, ABCDE is a regular pentagon and ABF is an equilateral triangle

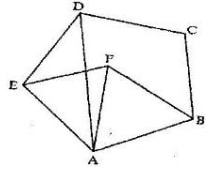
Find the size of
1. ∠DE
2. ∠AEF
3. ∠DAF
In this question use a pair of compasses and a ruler only
1. Construct triangle ABC such that AB = 6 cm, BC = 8cm and ∠ABC 135⁰(2 marks)
2. Construct the height of triangle ABC in a) above taking BC as the base (1 mark)
The size of an interior angle of a regular polygon is 3x⁰while its exterior angle is (x − 20)⁰. Find the number of sides of the polygon
Points L and M are equidistant from another point K. The bearing of L from K is 330⁰. The bearing of M from K is 220⁰. Calculate the bearing of M from L
Four points B,C,Q and D lie on the same plane point B is the 42 km due south- west of town Q. Point C is 50 km on a bearing of 5600 from Q. Point D is equidistant from B, Q and C.
1. Using the scale 1 cm represents 10 km, construct a diagram showing the position of B, C, Q and D
2. Determine the
  1. Distance between B and C
  2. Bearing D from B
Two aeroplanes P and Q, leave an airport at the same time flies on a bearing of 240⁰at 900km/hr while Q flies due East at 750 km/hr
1. Using a scale of 1 v cm drawing to show the positions of the aeroplanes after 40 minutes.
2. Use the scale drawing to find the distance between the two aeroplane after 40 minutes
3. Determine the bearing of
  1. P from Q ans 254⁰
  2. Q from P ans 74⁰
A port B is no a bearing of 080 from a port A and at a distance of 95 km. A submarine is stationed port D which is on a bearing of 200⁰from A, and a distance of 124 km from B. A ship leaves B and moves directly southwards to an island P, which is on a bearing of 140⁰from A. The submarine at D on realizing that the ship was heading for the island P decides to head straight for the island to intercept the ship.
Using a scale of 1 cm to represent 10 km, make a scale drawing showing the relative position of A, B D and P.
Hence find:
1. The distance from A and D
2. The bearing of the submarine from the ship when the ship was setting off from B
3. The baring of the island P from D
4. The distance the submarine had to cover to reach the island
Four towns R, T, K and G are such that T is 84 km directly to the north R and K is on a bearing of 295⁰ from R at a distance of 60 km. G is on a bearing of 340⁰from K and a distance of 30 km. Using a scale of 1 cm to represent 10 km, make an acute scale drawing to show the relative positions of the towns.
Find
1. The distance and bearing of T from K
2. The bearing of R from G
In the figure below, ABCDE is a regular pentagon and M is the midpoint of AB. DM intersects EB at N. (T7)
Find the size of
1. ∠BAE
2. ∠BED
3. ∠BNM
Use a ruler and compasses in this question. Draw a parallelogram ABCD in which AB = 8cm, BC = 6 cm and ∠BAD = 75^o. By construction, determine the perpendicular distance between AB and CD.
The interior angles of the hexagon are 2x⁰, ½x⁰, x + 40⁰, 110⁰, 130⁰and 160⁰. Find the value of the smallest angle.
The size of an interior angle of a regular polygon is 156⁰. Find the number of sides of the polygon.