Geometric Constructions - Mathematics Form 1 Notes

• Construction Instruments
• Construction of Perpendicular Lines
• Construction of Angles using a Ruler and a Pair of Compass Only
  • Construction of an Angle of 60
  • Construction of an Angle of 90
  • Construction of an Angle of 45
  • Construction of angles of multiple of 7½,  30, 15
• Construction of Parallel Lines
  • Using a Ruler and a Pair of Compass Only
• Proportional Division of lines
• Construction of Regular Polygons
  • Construction of a Regular Triangle
  • Construction of a Regular Quadrilateral
  • Construction of a Regular Pentagon.
• Construction of Irregular Polygons
  • Construction of Triangles
  • To Construct a Trapezium.
• Past KCSE Questions on the Topic

---

Construction Instruments

The following minimum set of instruments is required in order to construct good quality drawings:

• Two set squares.
• A protractor.
• A 15 cm or 150 mm ruler
• Compass
• Protractor
• Divider
• An eraser/rubber
• Two pencils - a 2H and an HB, together with some sharpening device – Razor blade or shaper.

---

Construction of Perpendicular Lines

To obtain the perpendicular bisector PQ

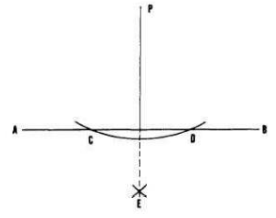
The figure below shows PQ as a perpendicular bisector of a given line AB.

• With A and B as centre, and using the same radius,draw arcs on either side of AB to intersect at P and Q.
• Join P to Q.

To construct a perpendicular line from a point

The figure below shows PE, a perpendicular from a point P to a given line AB.

• To drop a perpendicular line from point P to AB.
• Set the compass point at P and strike an arc intersecting AB at C and D.
• With C and D as centres and any radius larger than one-half of CD,
  
• Strike arcs intersecting at E.
• A line from P through E is perpendicular to AB.

 To construct a perpendicular line from a point

• Using P as centre and any convenient radius,draw arcs to intersect the lines at A and B.
• Using A as centre and a radius whose measure is greater than AP,draw an arc above the line.
• Using B as the centre and the same radius,draw an arc to interact the one in (ii) at point Q.
• Using a ruler ,draw PQ.

Construction of perpendicular lines using a set square.

• Two edges of a set square are perpendicular.
• They can be used to draw perpendicular lines.
• When one of the edges is put along a line, a line drawn along the other one is perpendicular to the given line.

To construct a perpendicular from a point p to a line

• Place a ruler along the line.
• Place one of the edges of a set square which form a right angle along the ruler.
• Slide the set square along the ruler until the other edge reaches p.
• Hold the set square firmly and draw the line through P to meet the line perpendicularly.
  

---

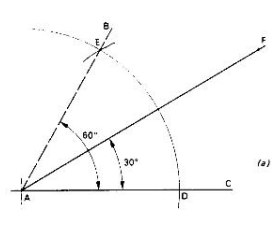
Construction of Angles Using a Ruler and a Pair of Compass Only

The basic angle from which all the others can be derived from is the 60⁰, 45⁰ and 90⁰

 

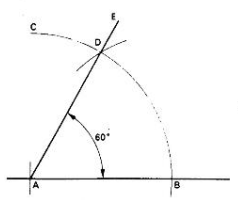
Construction of an Angle of 60⁰

• Let A be the apex of the angle
• With centre A draw an arc BC using a suitable radius.
• With b as the centre draw another arc to intersect arc BC at D.
• Draw a line AE through D. The angle EAC is 600

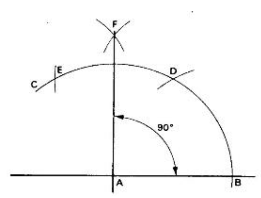
Construction of an Angle of 90⁰

• Let A be the apex of the angle.
• With centre A draw an arc BC of large radius.
• Draw an arc on BC using a suitable radius and mark it D.
• Using the same radius and point D as the centre draw an arc E.
• BD and DE are of the same radius.
• With centre D draw any arc F.
• With centre E draw an arc equal in radius to DF.
• Join AF with a straight line. Angle BAF is 900

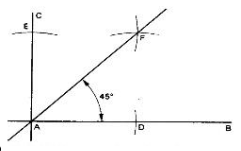
Construction of an Angle of 45⁰

• Draw AB and AC at right angles 45⁰ to each other.With centre A and with large radius ,draw an arc to cut AB at D and and AC at E.
• With centres E and D draw arcs of equal radius to intersect at Draw a straight line from A through Angle BAF is 45⁰

Construction of Angles of Multiple of 7½^o, 30⁰, 15⁰

The bisection of 60⁰ angle produces 30⁰ and the successive bisection of this angle produces 15⁰ which is bisected to produce 7½^o as shown below

• Draw AB and AC at 600 to each other as shown above.
• With centre A, and a large radius, draw an arc to cut AB at E and AC at D.
• With centres E and D draw arcs of equal radius to intersect at F.
• Draw a line from A through F.
• Angle CAF is 30⁰ half 60⁰.

To Construct 15⁰, 7½^o

• Draw AC and AF at 30⁰ to each other as described above.
• With centres G and D draw arcs of equal radius to intersect at H
• Draw a line from A through H
• Angle CAH is 15⁰.
• With centres J and D a further bisection can be made to give 7½⁰

---

Construction of Parallel Lines

• To construct a line through a given point and parallel to a given line, we may use a ruler and a pair of compass only, or a ruler and a set square.

Using a Ruler and A Pair of Compass Only

Parallelogram method

The line EP parallel to AC is constructed as follows:

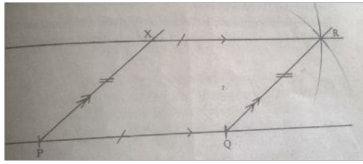
• With X as the centre and radius PQ, draw an arc.
• With Q as the centre and radius PX, draw another arc to cut the first arc at R.
• Join X to R.

---

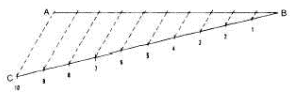
Proportional Division of Lines

Lines can be proportionately divided into a given number of equal parts by use of parallel lines.

To divide line AB

• Divide line AB into ten equal parts.
• Through b, draw a line CB of any convenient length at a suitable angle with AB.
• Using a pair of compasses, mark off,along BC ,ten equal intervals as shown above.
• Join C to A.By using a set square and a ruler, draw lines parallel to CA.
• The line is therefore divided ten equal parts or intervals.

---

Construction of Regular Polygons

A polygon is regular if all its sides and angles are equal ,otherwise it is irregular.

Note:

• For a polygon of n sides,the sum of interior angles is ( 2n − 4 ) right angles.The size of each interior angle of the regular polygon is therefore equal to (⁽²ⁿ⁻⁴⁾/n) × 90^o .
• The sum of exterior angles of any polygon is 3600.Each exterior angle of a regular polygon is therefore equal to ³⁶⁰/_n.

Construction of a Regular Triangle

• Draw AB, BC and CD equal in length to the sides of the required triangle
• With centre B and aradius AB draw the arc AF
• With centre C and radius CD draw the arc DG
• Where the arcs intersect at E is an apex of the triangle
• Join BE and CE with straight lines to form the triangle BCE

Construction of a Regular Quadrilateral

• Mark off one side of the square AB on the base line
• With centre A and radius AB draw the arc BC
• With centre B and radius AB draw the arc CD
• With centre E and radius AB step off F and G on arcs BC and AD respectively
• With centres E and F draw arcs of equal radius to intersect at H
• With centres E and G draw arcs of equal radius to intersect at J
• Erect perpendicular AH and BJ
• The arcs BC and AD cut the perpendiculars AH and BJ at K and L respectively
• To complete the square join K and L

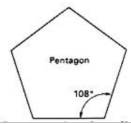
Construction of a Regular Pentagon.

To construct a regular pentagon ABCD of sides 4 cm.

Each of the interior angles = (⁽¹⁰⁻⁴⁾/₅) × 90 right angles = 108⁰

• Draw a line AB = 4 cm long.
• Draw angle ABC = 108⁰ and BC =4 cm
• Use the same method to locate points D and E

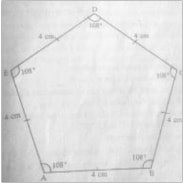
Note;

• Use the same procedure to construct other points.
  

---

Construction of Irregular Polygons

Construction of Triangles

To construct a triangle given the length of its sides

• Draw a line and mark a point A on it.
• On the line mark off with a pair of compass a point B, 3 cm from A.
• With B as the centre and radius 5 cm, draw an arc
• With A as the centre and radius 7 cm,draw another arc to intersect the arc in (iii) at C.Join A to C and B to C.

To construct a triangle, given the size of two angles and length of one side.

Construct a triangle ABC in which ∠ BAC = 60⁰, ∠ ABC = 50⁰ and BC = 4 cm.The sketch is shown below.

• Draw a line and mark a point B on it.
• Mark off a point C on the line, 4 cm from B.
• Using a protractor, measure an angle of = 50⁰ and = 70⁰ at B and C respectively.

To construct a triangle given two sides and one angle.

Given the lengths of two sides and the size of the included angle. Construct a triangle ABC, in which AB = 4 cm,BC =5 cm and ∠ ABC =60⁰.Draw a sketch as shown below.

• Draw a line BC = 5 cm along
• Measure an angle of = 60⁰ at B and mark off a point A, 4 cm from B.
• Join A to C.

---

To Construct a Trapezium.

The construction of a trapezium ABCD with AB = 8 cm ,BC = 5 cm, CD = 4cm and angle ABC = 60⁰ and AB = 8 cm

• Draw a line AB = 8 cm.
• Construct an Angle of = 60⁰ at B.
• Using B as the centre and radius of 5 cm, mark an arc to insect the line in (ii) at C.
• Through C , draw a line parallel to AB
• Using C as the centre and radius of 4 cm,Mark an arc to intersect the line in (iv) at D.
• Join D to A to form the trapezium.
  

---

Past KCSE Questions on the Topic

1. Using a ruler and a pair of compasses only,
   1. 1. Construct a triangle ABC in which AB = 9cm, AC = 6cm and angle BAC = 37½⁰
      2. Drop a perpendicular from C to meet AB at D. Measure CD and hence find the area of the triangle ABC
   2. Point E divides BC in the ratio 2:3. Using a ruler and Set Square only, determine point E. Measure AE.
2.  
   
   On the diagram, construct a circle to touch line AB at X and passes through the point C. (3 mks)
   
3. Using ruler and pair of compasses only for constructions in this question.
   1. Construct triangle ABC such that AB=AC=5.4cm and angle ABC=30⁰. Measure BC (4 mks)
   2. On the diagram above, a point P is always on the same side of BC as A. Draw the locus of P such that angle BAC is twice angle BPC (2 mks)
   3. Drop a perpendicular from A to meet BC at D. Measure AD (2 mks)
      
   4. Determine the locus Q on the same side of BC as A such that the area of triangle BQC = 9.4cm² (2 mks)
4. 1. Without using a protractor or set square, construct a triangle ABC in which AB = 4cm, BC = 6cm and ∠ABC = 67½⁰. Take AB as the base. (3mks)
      Measure AC.
   2. Draw a triangle A¹B¹C¹ which is indirectly congruent to triangle ABC. (3mks)
5. Construct triangle ABC in which AB = 4.4 cm, BC = 6.4 cm and AC = 7.4 cm. Construct an escribed circle opposite angle ACB 
   1. Measure the radius of the circle (5 mks)
   2. Measure the acute angle subtended at the centre of the circle by AB (1 mk)
   3. A point P moves such that it is always outside the circle but within triangle AOB, where O is the centre of the escribed circle. Show by shading the region within which P lies. (3mks)
      
6. 1. Using a ruler and a pair of compasses only, construct a parallelogram PQRS in which PQ = 8cm, QR = 6cm and PQR = 150⁰ (3 mks)
   2. Drop a perpendicular from S to meet PQ at B. Measure SB and hence calculate the area of the parallelogram. (5 mks)
   3. Mark a point A on BS produced such that the area of triangle APQ is equal to three quarters the area of the parallelogram (1 mk)
      
   4. Determine the height of the triangle (1mk)
7. Using a ruler and a pair of compasses only, construct triangle ABC in which AB = 6cm, BC = 8cm and angle ABC = 45^o. Drop a perpendicular from A to BC at M. Measure AM and AC (4mks)
8. 1. Using a ruler and a pair of compasses only to construct a trapezium ABCD such that AB = 12 cm, ∠DAB = 60^o, ∠ABC = 75^o, and AD = 7 cm (5 mks)
   2. From the point D drop a perpendicular to the line AB to meet the line at E. measure DE hence calculate the area of the trapezium (5 mks)
      
9. Using a pair of compasses and ruler only;
   1. Construct triangle ABC such that AB = 8cm, BC = 6cm and angle ABC = 30⁰.(3 marks)
   2. Measure the length of AC
   3. Draw a circle that touches the vertices A, B and C.
      
   4. Measure the radius of the circle
   5. Hence or otherwise, calculate the area of the circle outside the triangle.
      
10. Using a ruler and a pair of compasses only, construct the locus of a point P such that angle APB = 60⁰ on the line AB = 5cm. (4 mks)
11. Using a set square, ruler and pair of compases divide the given line into 5 equal portions. (3mks)
    
12. Using a ruler and a pair of compasses only, draw a parallelogram ABCD, such that angle DAB = 75⁰. Length AB = 6.0cm and BC = 4.0cm from point D, drop a perpendicular to meet line AB at N
    1. Measure length DN
    2. Find the area of the parallelogram (10 mks)
13. Using a ruler and a pair of compasses only, draw a parallelogram ABCD in which AB = 6cm, BC = 4cm and angle BAD = 60^o. By construction, determine the perpendicular distance betweenthe lines AB and CD
14. Without using a protractor, draw a triangle ABC where ∠CAB = 30^o, AC = 3.5cm and AB = 6cm. measure BC
15. 1. Using a ruler and a pair of compass only, construct a triangle ABC in which angle ABC = 37.5^o, BC =7cm and BA = 14cm
    2. Drop a perpendicular from A to BC produced and measure its height
    3. Use your height in (b) to find the area of the triangle ABC
    4. Use construction to find the radius of an inscribed circle of triangle ABC
16. In this question use a pair of compasses and a ruler only
    1. Construct triangle PQR such that PQ = 6 cm, QR = 8 cm and ∠PQR = 135°
    2. Construct the height of triangle PQR in (a) above, taking QR as the base
17. On the line AC shown below, point B lies above the line such that ∠BAC = 52.5^o and AB = 4.2cm. (Use a ruler and a pair of compasses for this question)
    
    
    1. Construct ∠BAC and mark point B
    2. Drop a perpendicular from B to meet the line AC at point F . Measure BF

Join our whatsapp group for latest updates

---

Download Geometric Constructions - Mathematics Form 1 Notes.

Tap Here to Download for 50/-

---

Get on WhatsApp for 50/-

---

Why download?

• ✔ To read offline at any time.
• ✔ To Print at your convenience
• ✔ Share Easily with Friends / Students

---