Angles and Plane Figures - Mathematics Form 1 Notes

• Introduction
• Representation of Points and Lines on a Plane
• Types of Angles
• Angles on a Straight Line.
• Angles at a Point
• Angles on a Transversal
• Angle Properties of Polygons
  • Triangles
  • Quadrilaterals
  • Proving That a Quadrilateral is a Parallelogram
  • Proving That a Quadrilateral is a Rectangle
  • Proving That a Quadrilateral is a Kite
  • Proving That a Quadrilateral is a Rhombus
  • Proving That a Quadrilateral is a Square
  • Proving That a Trapezoid is an Isosceles Trapezoid
• Past KCSE Questions on the topic

---

Introduction

• A flat surface such as the top of a table is called a plane. The intersection of any two straight lines is a point.

---

Representation of Points and Lines on a Plane

• A point is represented on a plane by a mark labelled by a capital letter. Through any two given points on a plane, only one straight line can be drawn.
  
  
• The line passes through points A and B and hence can be labelled line AB.

---

Types of Angles

• When two lines meet, they form an angle at a point. The point where the angle is formed is called the vertex of the angle. The symbol ∠is used to denote an angle.
  
  
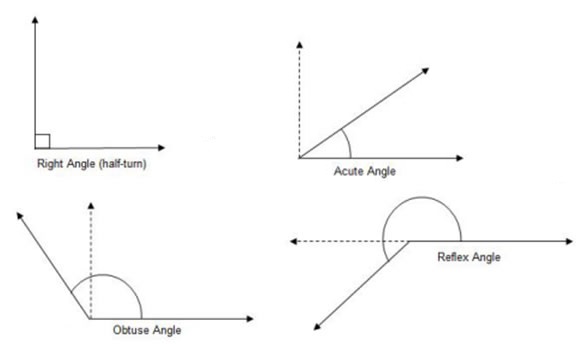
• To obtain the size of a reflex angle which cannot be read directly from a protractor ,the corresponding acute or obtuse angle is subtracted from 3600.If any two angles X and Y are such that:
  
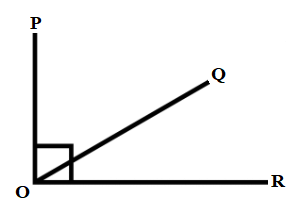
  1. Angle X + angle Y =900, the angles are said to be complementary angles. Each angle is then said to be the complement of the other.
     
  2. Angle X + angle Y =1800, the angles are said to be supplementary angles. Each angle is then said to be the supplement of the other.
• In the figure below ∠ POQ and ∠ ROQ are a pair of complementary angles.
  
  
• In the figure below ∠ DOF and ∠ FOE are a pair of supplementary angles.
  
  

---

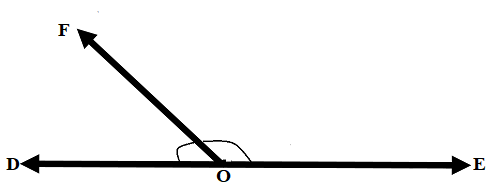
Angles on a Straight Line.

• The below shows a number of angles with a common vertex O. AOE is a straight line.
  
  
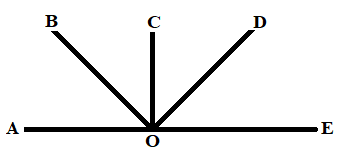
• Two angles on either side of a straight line and having a common vertex are referred to as adjacent angles.
• In the figure above:
  • ∠ AOB is adjacent to ∠ BOC
  • ∠ BOC is adjacent to ∠ COD
  • ∠COD is adjacent to ∠DOE
• Angles on a straight line add up to180⁰.

---

Angles at a Point

• Two intersecting straight lines form four angles having a common vertex. The angles which are on opposite sides of the vertex are called vertically opposite angles.
• Consider the following:
  
  
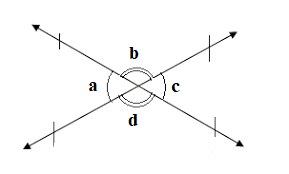
• In the figure above ∠ COB and ∠AOC are adjacent angles on a straight line. We can now show that a = c as follows:
  • a + b = 180⁰(Angles on a straight line)
  • c + d = 180⁰(Angles on a straight line)
• So, a + b + c + d =180⁰+180⁰ =360⁰
• This shows that angles at a point add up to360⁰

---

Angles on a Transversal

• A transversal is a line that cuts across two parallel lines.
  
  
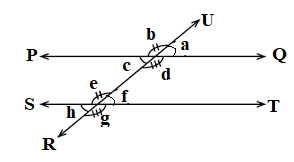
• In the above figure PQ and ST are parallel lines and RU cuts through them. RU is a transversal.
• Name:
  1. Corresponding angles are Angles b and e, c and h, a and f, d and g.
  2. Alternate angles a and c, f and h, b and d, e and g.
  3. Co-interior or allied angles are f and d, c and e.

---

Angle Properties of Polygons

• A polygon is a plan figure bordered by three or more straight lines

Triangles

• A triangle is a three sided plane figure. The sum of the three angles of a triangle add up to 180⁰.triangles are classified on the basis of either angles sides.
  
  1. A triangle in which one of the angles is 900 is called a right angled triangle.
  2. A scalene triangle is one in which all the sides and angles are not equal.
  3. An isosceles triangle is one in which two sides are equal and the equal sides make equal angles with the third side.
  4. An equilateral triangle is one in which all the side are equal and all the angles are equal

 

Exterior properties of a triangle

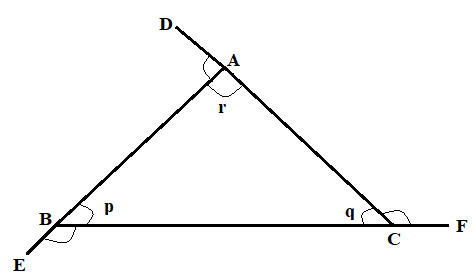
Angle DAB = p + q.
Similarly, Angle EBC = r + q and angle FCA = r + p.
But p + q + r = 180⁰
But p + q + r = 180⁰
Therefore angle DAB + angle EBC + angle FCA = 2p +2q + 2r
=2(p +q +r)
= 2 x 180⁰
= 360⁰

In general the sum of all the exterior angles of a triangle is 3600.

Quadrilaterals

• A quadrilateral is a four –sided plan figure. The interior angles of a quadrilateral add put 3600.Quadrilaterals are also classified in terms of sides and angles.

Properties of quadrilaterals

Properties of Parallelograms

In a parallelogram,

1. The parallel sides are parallel by definition.
2. The opposite sides are congruent.
3. The opposite angles are congruent.
4. The diagonals bisect each other.
5. Any pair of consecutive angles are supplementary.

Properties of Rectangles

In a rectangle,

1. All the properties of a parallelogram apply by definition.
2. All angles are right angles.
3. The diagonals are congruent.

Properties of a kite

1. Two disjoint pairs of consecutive sides are congruent by definition.
2. The diagonals are perpendicular.
3. One diagonal is the perpendicular bisector of the other.
4. One of the diagonals bisects a pair of opposite angles.
5. One pair of opposite angles are congruent.

Properties of Rhombuses

In a rhombus,

1. Allthe properties of a parallelogram apply by definition.
2. Two consecutive sides are congruent by definition.
3. All sides are congruent.
4. The diagonals bisect the angles.
5. The diagonals are perpendicular bisectors of each other.
6. The diagonals divide the rhombus into four congruent right triangles.

Properties of Squares

In a square,

1. All the properties of a rectangle apply by definition.
2. All the properties of a rhombus apply by definition.
3. The diagonals form four isosceles right triangles.

Properties of Isosceles Trapezoids

In an isosceles trapezoid,

1. The legs are congruent by definition.
2. The bases are parallel by definition.
3. The lower base angles are congruent.
4. The upper base angles are congruent.
5. The diagonals are congruent.
6. Any lower base angle is supplementary to any upper base angle.

Proving That a Quadrilateral is a Parallelogram

Any one of the following methods might be used to prove that a quadrilateral is a parallelogram.

1. If both pairs of opposite sides of a quadrilateral are parallel, then it is a parallelogram (definition).
2. If both pairs of opposite sides of a quadrilateral are congruent, then it is a parallelogram.
3. If one pair of opposite sides of a quadrilateral are both parallel and congruent, then it is a parallelogram.
4. If the diagonals of a quadrilateral bisect each other, then the it is a parallelogram.
5. If both pairs of opposite angles of a quadrilateral are congruent, then it is a parallelogram.

Proving That a Quadrilateral is a Rectangle

One can prove that a quadrilateral is a rectangle by first showing that it is a parallelogram and then using either of the following methods to complete the proof.

1. If a parallelogram contains at least one right angle, then it is a rectangle (definition).
2. If the diagonals of a parallelogram are congruent, then it is a rectangle.
   One can also show that a quadrilateral is a rectangle without first showing that it is a parallelogram.
3. If all four angles of a quadrilateral are right angles, then it is a rectangle.
   

Proving That a Quadrilateral is a Kite

To prove that a quadrilateral is a kite, either of the following methods can be used.

1. If two disjoint pairs of consecutive sides of a quadrilateral are congruent, then it is a kite (definition).
2. If one of the diagonals of a quadrilateral is the perpendicular bisector of the other diagonal, then it is a kite.

Proving That a Quadrilateral is a Rhombus

To prove that a quadrilateral is a rhombus, one may show that it is a parallelogram and then apply either of the following methods.

1. If a parallelogram contains a pair of consecutive sides that are congruent, then it is a rhombus (definition).
2. If either diagonal of a parallelogram bisects two angles of the parallelogram, then it is a rhombus.
   One can also prove that a quadrilateral is a rhombus without first showing that it is a parallelogram.
3. If the diagonals of a quadrilateral are perpendicular bisectors of each other, then it is a rhombus.

 

Proving That a Quadrilateral is a Square

The following method can be used to prove that a quadrilateral is a square:

• If a quadrilateral is both a rectangle and a rhombus, then it is a square.
  

Proving That a Trapezoid is an Isosceles Trapezoid

Any one of the following methods can be used to prove that a trapezoid is isosceles.

1. If the nonparallel sides of a trapezoid are congruent, then it is isosceles (definition).
2. If the lower or upper base angles of a trapezoid are congruent, then it is isosceles.
3. If the diagonals of a trapezoid are congruent, then it is isosceles.

Note:

• If a polygon has n sides, then the sum of interior angles (2n -4) right angles.
• The sum of exterior angles of any polygon is 360⁰.
• A triangle is said to be regular if all its sides and all its interior angles are equal.

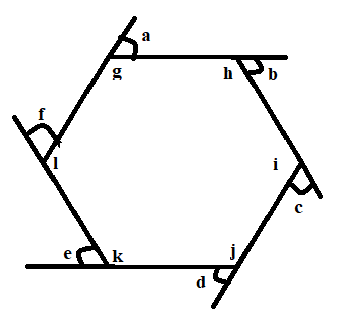
The figure below is a hexagon with interior angles g ,h ,I ,k and I and exterior angles a, b ,c ,d ,e ,and f.

---

Past KCSE Questions on the Topic

1. In the figure below, lines AB and LM are parallel.
   
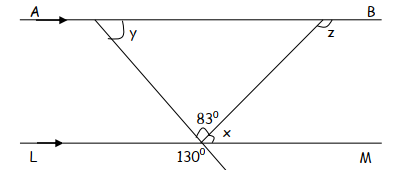
   Find the values of the angles marked x, y and z (3 mks)

Join our whatsapp group for latest updates

---

Download Angles and Plane Figures - Mathematics Form 1 Notes.

Tap Here to Download for 50/-

---

Get on WhatsApp for 50/-

---

Why download?

• ✔ To read offline at any time.
• ✔ To Print at your convenience
• ✔ Share Easily with Friends / Students

---