Coordinates and Graphs - Mathematics Form 1 Notes

• Introduction
• The Cartesian Plane
• The Graph of a Straight Line
• Graphing Solutions of Simultaneous Linear Equation
• General Graphs
• Revision Questions on the Topic

Introduction

• The position of a point in a plan is located using an ordered pair of numbers called co- ordinates and written in the form (x, y).The first number represents the distance along the x axis and is called the x co-ordinates.
• The second number represents distance along the y axis and it’s called the y coordinates.
• The x and y coordinates intersects at (0, 0) a point called the origin. The system of locating points using two axes at right angles is called Cartesian plan system.
• To locate a point on the Cartesian plane, move along the x-axis to the number indicated by the x-coordinate and then along the y-axis to the number indicated by the y-coordinate. For example, to locate the point with coordinates (1 , 2), move 1 unit to the right of the origin and then 2 units up

The Cartesian Plane

Example

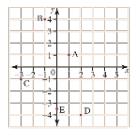
Write the Cartesian coordinates of the points A to E marked on the Cartesian plane below

Solution

1. Trace along the x - axis to find the first number, and then along the y axis to find the second number
   • Point A is at 1 on the x - axis and 1 on the y - axis
   • Point B is at −1 on the x - axis and 4 on the y - axis
   • Point C is at −3 on the x - axis and −1 on the y - axis
   • Point D is at 2 on the x - axis and −4 on the y - axis
   • Point E is at 0 on the x - axis and −3¹/₂ on the y - axis
2. Write each point as a pair of coordinates
   A(1,1), B(−1,4), C(−3,−1), D(2, −4), E(0, −3¹/₂)

The Graph of a Straight Line

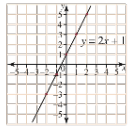
Consider the Linear equation y = 2x + 1. Some corresponding values of x and y are given in the table below.

If we plot the points webnotice that they all lie in a straight line.

Solution

Step 1 write the rule

y = 2x + 1

Step 2 Draw a table and choose simple x values
Step 3 Use the rule to find each y value and enter then in the table.
E.g. when x = -2, y= 2 x -2 + 1 = −3.
when x = −1 ,y= 2 x − 1 + 1 = −1
step 4 Draw a Cartesian plan and plot the points.
Step 5 Join the points to form a straight line and label the grap

Note:

• Two points are sufficient to determine a straight line, but we use the third point as a check.
• It is advisable to choose points which can be plotted easily.

Graphing Solutions of Simultaneous Linear Equation

• The graphs of the form ax + by = c represents a straight line. When two linear equations are represented on the same Cartesian plan, their graphs may or may not intersect. For example, in solving the simultaneous equations x + 3y = 5 and 5x + 7y = 9 graphically, the graphs of the two equation are drawn.
  
  
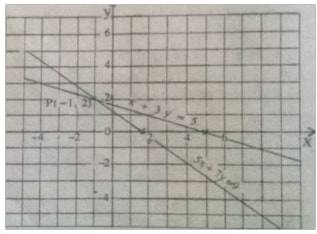
• The two lines intersect at p (- 1 , 2).The solution to the simultaneous equations is, therefore, x = - 1 and y = 2.
  

General Graphs

• Graphs are applied widely in science and many other fields. The graphs should theirfoe be drawn in a way that convey information easily and accurately. The most of important technique of drawing graphs is the choice of appropriate scale.
• A good scale is one which uses most of the graph page and enables us to plot points and read off values easily and accurately.
• Avoid scales which:
  • Give tiny graphs.
  • Cannot accommodate all the data in the table.
• It is good practice to:
  • Label the axes clearly.
  • Give the title of the graph.

Revision Questions on the Topic

1. Copy and complete the table and hence draw the corresponding graph.
   Y= 4x + 3
   

   x	-2	-1	0	1	2
   y

2. Draw the graph of the following:
   1. y + 2x =5
   2. ^y/₂ + 2x =5