Linear Motion Questions and Answers - Physics Form 3 Topical Revision

Questions

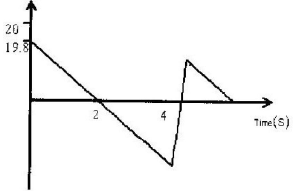
1. The diagram below shows part of the motion of a tennis ball, which is projected vertically upwards from the ground and allowed to bounce on the ground. Use this information to answer questions that follow.
   
   
   1. Describe the motion of the ball relating it to different positions of the ball along the following AB, BC, CDE.
   2. From the graph, calculate the acceleration due to gravity.
   3. How high does the ball rise initially?
   4. Explain why E is not at the same level as A.
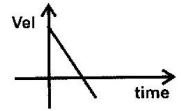
2. Sketch a velocity- time graph showing the motion of a ball vertically upwards with an initial velocity of u.
3. Calculate the acceleration shown by the tickers-tape that was made using a ticker timer vibrating at 50Hz.
   
4. What is the difference between speed and velocity?
5. An object is projected vertically upwards at a speed of 15m/s. How long will it take to return to the same level of projection?
6. A block slides off a horizontal table 4 meters high with a velocity of 12-m/s. Find:
   1. The horizontal distance from the table at which the block hits the floor.
   2. The horizontal and vertical components of the velocity when it reaches the floor.
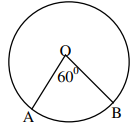
7. A particle initially at A moves along an arc AB of a horizontal circle of radius 4m and centre O.A is south of O and angle AOB is 600. Determine the displacement AB.
   
8. The figure represents dots made by a ticker-timer. The dots were made at a frequency of 50 dots per second. (Diagram not drawn to scale)
   
   
   1. What is time interval between two consecutive dots?
   2. The arrow on the tape indicates the dots made at time t = 0. Copy the diagram and indicate in a similar way the dots made at t= 0.1s, 0.2s, 0.3s.
   3. Determine the average velocities of the tape over time intervals -0.02s to 0.02s, 0.08s to 0.12s, 0.18s to 0.22s and 0.28s to 0.32s
   4. Draw a suitable graph and from it determine the acceleration of the tape.
9. A mass is projected horizontally from height of 5m above the ground with a velocity of 30m/s. Calculate:
   1. The time taken to reach the ground
   2. The horizontal distance traveled before hitting the ground
   3. The vertical velocity with which the mass hits the ground
10. The data in the table below represents the motion over a period of 7 seconds
    

    Time s	0	1	2	3	4	5	6	7
    D is m	0	20	40	60	80	95	105	110

    
    
    1. Plot on graph paper a graph of displacement (y-axis) against time.
    2. Describe the motion of the vehicle for the first 4 seconds.
    3. Determine the velocities at 4.5s and 6.5 s. Hence or otherwise determine the average acceleration of the vehicle over this time interval.
11.  
    1. A body accelerates uniformly from initial velocity, U to the final velocity V, in time t, the distance traveled during this time interval is S. If the acceleration is shown by the letter a, show that;
       1. V = U + at
       2. s = ut + ½at²
       3. V² = U² + 2 as
    2. A body initially moving at 50m/s decelerates uniformly at 2m/s until it come to rest. What distance does it cover from the time it started to decelerate?
12. An object dropped from a height h attains a velocity of 6m/s just before hitting the ground, find the value of h.
13.  
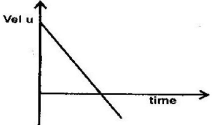
    1. A stone is thrown vertically upwards from the edge of a platform eventually the stone lands without bouncing on the ground below the platform. Taking the upward velocity to be positive, sketch the velocity-time graph of the motion of the stone.
    2. A car can be brought to rest from a speed of 200m/s in a time of 2s.
       1. Calculate the average deceleration
       2. If the driver reaction time is 0.2s, Determine the shortest stopping distance.
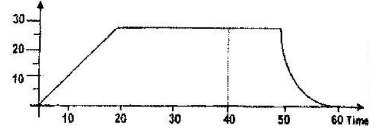
14. The figure shows a speed-time graph for part of the journey of a motorcar.
    
    Determine the distance the car travels in the first 40 seconds
15. Draw axes and sketch a graph of velocity (v versus time (t) for uniformly accelerated motion given that when t = 0, v is greater than zero.
16.  
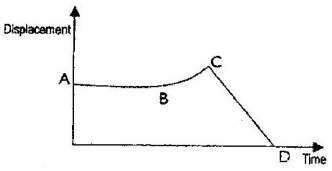
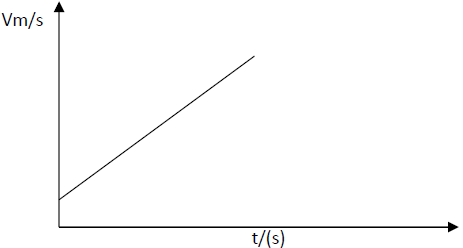
    1. The figure below shows the displacement time graph of the motion of a particle.
       
       State the nature of the motion of the particle between:
       1. A and B
       2. B and C
       3. C and D
    2. A ball is thrown horizontally from the top of a vertical tower and strikes the ground at a point 50m from the bottom of the tower. Given that the height of the tower is 45m, determine the;-
       1. Time taken by the ball to hit the ground
       2. Initial horizontal velocity of the ball.
       3. Vertical velocity of the ball, just before striking the ground. (Take acceleration due to gravity g as 10ms^-2)
17. The graph below shows how the velocity varies with time for a body thrown vertically upwards.
    
    Determine the total distance moved by the body. (3mks)
18. A bullet is fired horizontally from a platform 15m high. If the initial speed is 300ms^-1, determine the maximum horizontal distance covered by the bullet. (3mks)
19. The figure below shows the velocity-time graph for a small metal sphere falling through a viscous fluid.
    
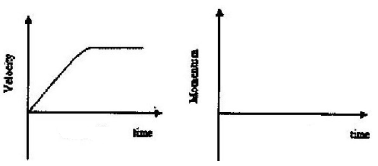
    On the axes provided sketch the graph of momentum against time for the same mass (1mk)
20. The graph in the figure below shows the velocity of a car in the first 8 seconds as it accelerates from rest along a straight line. 
    
    
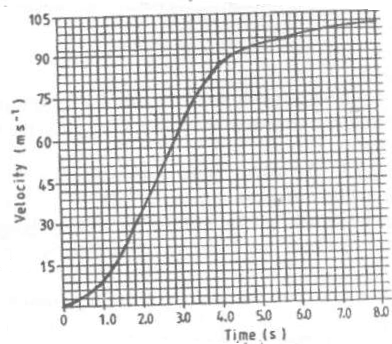
    1. Determine the distance traveled 3.0 seconds after the start. (3mks)
    2. Determine the acceleration of the car at 4.0 seconds. (2mks)
21. A bomber flying horizontally at 100m/s releases a bomb from a height of 300m. Calculate:
    1.  Time taken for the bomb to hit the ground.
    2. The horizontal distance traveled when hitting the ground.
    3. The magnitude and direction of the velocity when hitting the ground?
22. An airplane is flying horizontally over a camp at 250m/s and drops a pack. How far from the camp will the pack land if the plane was flying 300m above the ground?
23. An object is projected horizontally at a velocity of 40m/s from a cliff 20m high. Calculate:
    1. The time taken to hit the ground
    2. The distance from the foot of the cliff when the object hits the ground.
24. A ball-bearing X is dropped vertically downwards, from the edge of a table and it takes 0.5s to hit the floor below. Another bearing Y leaves the edge of the table horizontally with a velocity of 5m/s. find:
    1. The time taken for bearing Y to reach the floor.
    2. The horizontal distance traveled by Y before hitting the floor.
    3. The height of the table-top above the floor level.
25. A helicopter, which was ascending vertically at a steady velocity of 20m/s, released a parcel that took 20 second to reach the ground.
    1. State the direction in which the parcel moved immediately it was released.
    2. Calculate the time taken by the parcel to reach the ground from the maximum height.
    3. Calculate the velocity of the parcel when it strikes the ground.
    4. Calculate the maximum height above the ground the parcel reached.
    5. What was the height of the helicopter at the instant the parcel was dropped.
26. A stone is thrown horizontally from a building that is 50 m high above a horizontal ground. The stone hits the ground at a point, which is 65m from the foot of the building. Calculate the initial speed of the stone.

Answers

1.  
   1. AB - ball rising to max height
      BC - ball falling to ground
      CDE- ball rebouncing/ changing velocity from +ve to –ve
   2. Acceleration = gradient = 19.8 = 9.9 m/s²
   3. Displacement = area
      = ½ x 2 x 19.8 = 19.8m
   4. Upon hitting the ground the ball looses some energy.
2.  
   
3. Time interval between any two dots = ¹/₅₀ =0.02s 
   Dist d₁ between 1st and 2nd dots = 2.2 cm
   = V₁ = 0.022 m = 1.1ms^-1 
               0.02 s
   Dist d₂ between 4th and 5th dots = 3.3cm, v₂ = 0.033 =1.65m/s
                                                                          0.02
   Note: the average velocity between any two dots = the velocity of a point half way between the pts. Label the pts A.B.C.D & E label a pt x and y half way between D and E respectively (i.e. halfway in time not distance)
   T x y = 0.01+ 0.02 x 2 + 0.01 = 0.06s 
   Therefore a = V₂ – V =1.65 − 1.1 = 0.54 = 9m/s² 
                            T           0.06          0.06
4. Speed is a scalar quantity while velocity is a vector quality.
5. v = u +at 
   0 =15 − 10t
   t= 15s (to max height) therefore total time = 2 x 1.5=3s
6.  
   1. Initial vertical velocity = 0, a=10, S=4m 
      Therefore: S= ut + ¹/₂ gt² 
      4 = 0+5t² 
      t = 0.8944
      Range (horizontal dist) = initial vel. (constant) x time
      = 12 x 0.8944 
      = 10.73m
   2. Initial and final horizontal velocities are equal =12m/s 
      Final vertical velocity = v = u + at
      v = 0 + 10 x 0.8944
      v = 8.944 m/s
7. OA = OB therefore OAB is isosceles
   Displacement is distance covered in a straight line i.e. AB since <OBA = AOB = 60 then the triangle is equilateral. So AB=AO=4m
8.  
   1. t = ¹/_f = ¹/₅₀ = 0.02s
   2. 0.1s is equal to 5 time intervals
      
      Diagram not drawn to scale (refer from the actual paper)
   3. Average vel between - 0.02S to 0.02 = X₁/_0.04 (=vel at t=0s)
      Similarly for 0.08 to 0.12, v₂ = X₂ = vel at t = 0.1s 
                                                   0.04
      For 0.18 to 0.22, v₃ = X₃ = vel at t = 0.2s
                                     0.04 
      For 0.28 to 0.32, v₄ = X₄ = vel at t= 0.3s
                                     0.04
   4. Note: The average velocities above represent the actual velocities halfway between the three dots.
      Tabulating the results
      
      

      Time	0	0.1	0.2	0.3
      Velocity (v)	V1	V2	V3	V4

      Plot v against t and draw the best line of fit. Find gradient = acceleration.
9.  
   1. Initial vertical velocity = 0, a = g; s= 5m 
      S=ut + ¹/₂gt² 
      S = 0 + 5t² 
      T= 1s
   2.  Range = Uμ x t = 30 x 1 = 30m
   3. V_v =U_v + gt 
      V_v = 0 + 10 x 1 = 10m/s
10.  
    1. Plot the graph
       Note: the graph is a straight line for the first 4 seconds then a curve
    2. Velocity constant
    3. Draw tangents to the graph at t = 4, 5 s and t = 6.5 s. Obtains the gradients of the tangents g1 and g2 which are equal to velocities at t = 4.5 s (V1) and at t
       = 6.5s (V₂) 
       Acc = V₂ - V₁ ≈ 4.9m/s²
                6.5 - 4.5
11.  
    1.  
       1. acc = (change in ^vel/_time) 
          a = (v - u)  .
                    t  
          v = u + at.... (i)
       2. Displacement = average vel x time
          s = (u + u + at)t = ut +¹/₂at² ... (ii)
                       2
       3. Square equation (i) 
          v² = (u + at)² 
          v² = u² + 2aut + a²t² 
          Factorizing v² = u² + 2a (ut + ¹/₂at²) 
          but ut + ¹/₂at² = s (from equ.(ii) . 
          v² = u² + 2as
    2. u = 50m/s
       a =2m/s² v= 0
       v² = u² + 2as 
       0 = 2500 - 4s 
       S= 625m
12. mgh = ¹/₂mv^{2 
    1}/₂ v² = gh 
    ¹/₂ x ³⁶/₁₀ = h 
    h = 1.8m
13.  
    1.  
       
    2.  
       1. u = 20m/s, t=2s, v=0
          V = u + at
          0 = 20 + a x 2
          A = -10m/s
          Deceleration = 10m/s² 
       2. Distance traveled before starting to break = 0.2 x 20 = 4m
          Distance moved after breaks are applied,
          U=20, a=-10, v=0
          v² = u² + 2as
          0 = 400 - 20s
          s = 20m
          Total distance = 24m 
14. S = ¹/₂(a+b)h
    h = ¹/₂(40+20)(25) = 750 m
15.  
     
16.  
    1.  
       1. Particle stationary/at rest.
       2. Increasing vel. (grad=vel)
       3. Particle moving at cost. vel in the opp. direction i.e. towards origin.
    2.  
       1. U_v=0, S=45m, a=10m/s² t=? 
          S =ut+ ¹/₂at² 
          45 = 0+5t² 
          t=3s
       2. Range =50m 
          t=35
          U_m = ⁵⁰/₃ = 16.67m/s 
       3. V_v = U_v + at 
          V_v = 0 + 10 x 3 
          V_v = 30m/s
17. Total distance = area bound by x-axis and the line of graph 
    Total distance = 2 x 12 x 2 x 20 = 40 m
    Note: Since distance is scalar quantity the -ve area is taken to be +ve.
18. s=15, U_m=300m/s, a_v=10m/s², U_v=0m/s 
    Therefore s=ut + ¹/₂at² 
    15 = 0 + 5t² 
    t = √3
    t=1.732s
    Therefore d=U_H x t=300 x 1.732 = 519.62 m
19.  
    
    
20.  
    1. Distance = area under curve between 0 and 3.0 second.
       = 120 x 3x 0.2 = 72m
       Accept 70.5, 73.5, 76.5
    2. Acceleration = slope of graph at t = 4.0s 
         16 x 3 
       17 x 0.2 = 14.11 m/s²
21.  
    1. 24.45s
    2. 2445m
    3. 264.2 m/s or 67.8⁰ to the horizontal
22. 1936.5m
23.  
    1. 2s
    2. 80
24.  
    1. 0.5s
    2. 2.5m
    3. 1.25m
25.  
    1. Upwards
    2. 18s
    3. 180m/s
    4. 1620m
    5. 1,600m
26. 20.6m/s