Refraction of Light Questions and Answers - Physics Form 3 Topical Revision

Questions

1. The diagram below shows a transparent water tank containing water. An electric light is fixed at corner A of the tank. A light ray from the slit shines on the water surface BC at an angle of 48⁰ as shown
   
   
   1.  
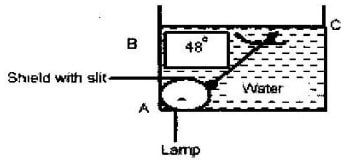
      1. Determine the angle of refraction for the ray shown in the diagram.
      2. Complete the diagram to show the refracted ray.
   2. Determine the angle of incidence for which the angle of refraction is 90⁰
   3. Calculate the speed of light in water (nw = ⁴/₃, C= 3 x 10⁸ m/s)
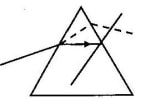
2. The figure shows the path of a yellow light through a glass prism. The speed of yellow light in the prism is 1.88 x 10⁸ m/s.
   
   
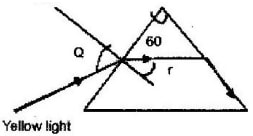
   1. Determine the refractive index of the prism material for the light. (Speed of light in vacuum = 3.0 x 10⁸ ms^-1)
   2. Show on the figure the critical angle C and determine the value.
   3. Given that r= 21.2⁰, determine angle Q.
   4. On the same figure, sketch the path of the light after striking the prism if the prism was replaced by another of similar shape but lower refractive index. (Use dotted line for your answer).
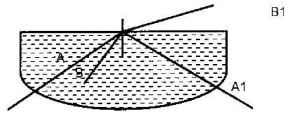
3. The figure below shows two rays A and B entering a semi circular glass block which has critical angle of 42⁰. The rays are incident at an air glass boundary at point O
   
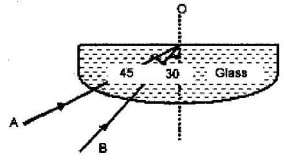
   Complete the path of the two rays from point O. Label A₁ and B₁ the corresponding rays.
4. A ray of light is directed at an angle of 50⁰ on to a liquid-air boundary. 
   The refractive index of the liquid is 1.4.
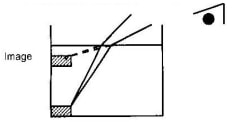
   Show on a diagram the patch taken by the ray on striking the liquid-air boundary. Show how you arrive at your answer.
5. The figure below shows a coin placed in a large empty container. An observer looking into the container from the position shown is unable to see the coin.
   
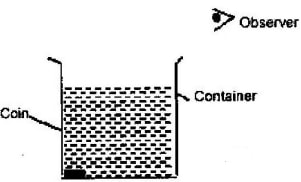
   Sketch two rays from a point on the coin to show how the observer is able to see the image of the coin after the container is filled with water.
6. The figure below show a ray of light incident on the face of a water prism.
   
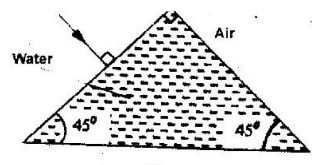
   Sketch the path of the rays as it passes through the prism. Critical angle for water is 49⁰ (1mk)
7. Calculate the refractive index of glass given that the velocity of light in air is 3x 10⁸ ms^-1 and velocity of light in glass is 2.4 x 10⁸ ms^-1.
8. The real thickness of crown glass block of refractive index 1.58 is 10 cm. Calculate the apparent thickness of the glass.
9. You are provided with the following;
   - A 50 cm beaker full of water.
   - Stand and clangs
   - A half metre rule
   - 2 optical pins
   - Cork
   1. Explain briefly how you would determine the refraction index of water using the materials provided.
   2. The data below shows the results obtained when such an experiment was performed by form three students using various values of real depths, Y of a liquid.
      

      Real depth cm	30	50	70	90	110	130
      Apparent depth cm	22	37	52	66	81	96

      1. Plot a graph of the real depth (y-axis) against apparent depth.
      2. From the graph, determine the refractive index of the liquid.
10. Paraffin has a greater refractive index than that of water. Comment about the relative velocity of light in paraffin and in water. 
11.  
    1. State snell's law
    2. A ray of light travels from air into medium 1 and 2 as shown.
       
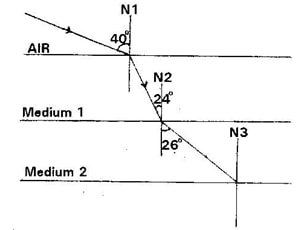
       Calculate;
       1. The refractive index of medium 1.
       2. Critical angle of medium 1
       3. The refractive index of medium 2 relative to medium (₁n₂)
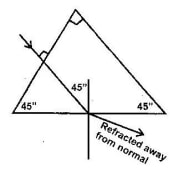
12. Explain with the aid of a diagram, how a suitable glass prism may be used to turn a ray of light 180⁰ 
13. What measurable quantity is associated with colour of light?
14. State TWO uses of total internal reflection.
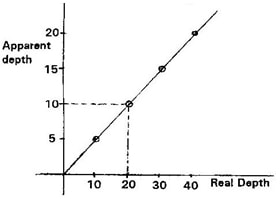
15. The graph shown below shows, the apparent depth (y-axis) against real depth. Use it to calculate the refractive index of glass.
    
16. The refractive index for air-water boundary is ⁴/₃. Calculate the critical cycle for water–air interface.

Answers

1.  
   1.  
      1. Sin 48 = 3 
         Sin r       4 
         Sin r = 0.9906
         = 82.2⁰
   2. Sin C = ¹/_n = 0.75
      C= 48.60
      i.e. when r= 90, I= C
      Va = n
      Vw
      3 x 10⁸ = 4
       Vw         3
      ∴ Vw = 2.25 x 10⁸ m/s
2.  
   1. n= Va = 3.00 x 10⁸ = 1.6
           Vp    1.88 x 10⁸ 
   2.  
      
      Sin C = ¹/_1.6
      C = 38.8
   3. Sin Q = 1.6
      Sin 21.2
      Q= 35.4⁰
3.  
   
4. Sin C= ¹/_n = ¹/_1.4
   C= 45.6
   ∴ Total internal reflection will take place.
5.  
   
6.  
   
7. _an_g = Velocity of light in air
   = Velocity of light in glass
   = 3x 10⁸
   = 2.4 x 10⁸
   = 1.25
8. η_g =    Real thickness    
          Apparent thickness
   1.58= ¹⁰/_{Apparent thickness}
   Apparent thickness = ¹⁰/_1.58 = 6.33cm
   The apparent thickness of crown glass block = 6.33cm
9.  
   1.  
      
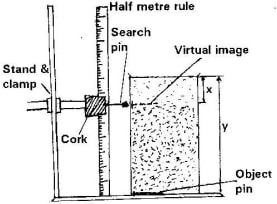
      - Set the apparatus as shown above.
      - Adjust the search pin to no-parallax position.
      - Using the metre rule, measure the apparatus distance x and the real depth y of the water.
      - Repeat the experiment for other values of y
      - Plot a graph of y against x.
      Refractive index = gradient of graph
      =  Real depth  
       Apparent depth
      η_w = ^y/_x
   2.  
      1. Graph
         
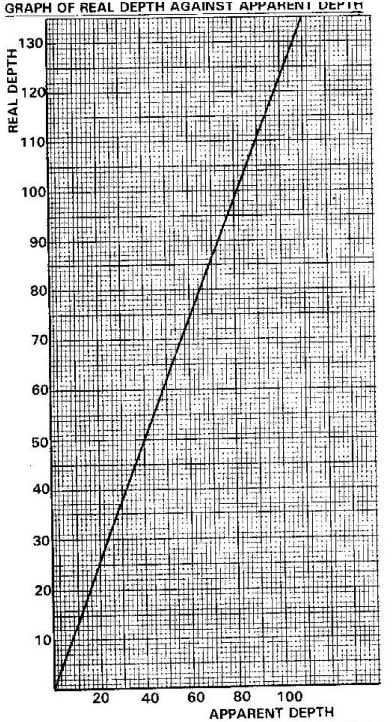
      2. η₁ =  Real depth   = gradient of the graph
               Apparent depth
         Gradient = 135 = 1.35
                          100
         ∴ Refractive index, η₁=1.35
10. Bending of light is more in paraffin than in water.
    Thus speed of light in paraffin is less than that in water.
11.  
    1. Ratio of sine of angle of incidence to sine of angle of refraction is always a constant i.e.
       η = Sin I in medium 1
             Sin r in medium 2
    2.  
       1. _aη₁ = Sin i
                   sin r
          = sin 40⁰ = 0.6428
          Sin 24⁰ = 0.4067
          = 1.581
       2.  _aη₁ = ¹/_{Sin C} Where C is the critical angle then
          1.581= ¹/_{Sin C}
          Sin C =¹/_1.581 = 0.6325
          C = sin^-1 0.6325
          = 39.23⁰
          Critical angle = 39.23⁰
       3. ₁η₂ = sin I in 1
                   Sin r in 2
          = Sin 24⁰ = 0.4067
             Sin 26⁰    0.4384
          = 0.9277
12. Solution;
    Use a right angled prism.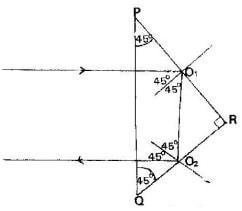
    
    Ray meets longest side of prism at 90⁰ and passes undeviated. It makes an angle of 45⁰ with normal at O₁ and is totally internally reflected. The reflected ray makes an angle of 45⁰ with normal at O₂ and is totally reflected as shown. Total deviation = (4 x 45)⁰ = 180⁰
13. Frequency or wavelength
14. Used in;
    • Prism periscope
    • Optical fibre
    • Prism binocular
15. Solution;
    Gradient of the graph = Apparent depth
                                           Real depth
    = ¹⁰/₂₀ = ½ 
    But refractive index =   Real depth   
                                    Apparent depth
    η_g = ¹/_gradient
    ∴ Refractive index of glass = 2
16. Solution;
    For light passing from water to air then 
    _wη_g = ³/₄