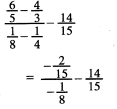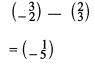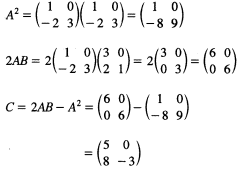KCSE 2012 Mathematics Paper 1 with Marking Scheme

SECTION 1 [ 50 marks]

1. Without using a calculator, evaluate (4 marks)
2. Find the reciprocal of 0.216 correct to 3 decimal places, hence evaluate
    (3 marks)
3. Expand and simplify the expression (2x²-3y³ )²+12x²y³ (2 marks)
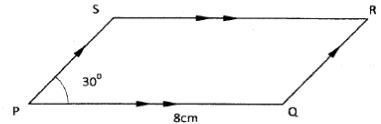
4. In the parallelogram PQRS shown below ,PQ=8 cm and angle SPQ =30⁰
   
   If the area of the parallelogram is 24 cm , find its perimeter. (3 marks)
5. Given that 9^2Y×2^X=72, find the values of x and y . (3 marks)
6. Three bells rings at intervals of 9 minutes , 15 minutes and 21 minutes. The bells will next ring together at 11.00 pm, Find the time the bells had last rang together. (3 marks)
7. Koech left home to a shopping center 12 km away, running at 8km/h .Fifteen minutes later, mutual left the same home and cycled to the shopping center at 20km/h. Calculate the distance to the shopping center at which Mutua caught up with Koech. (3 marks)
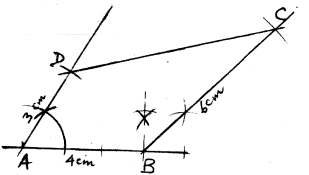
8. Using a pair of compass and a ruler only, construct a quadrilateral ABCD in which AB =4cm, BC=6cm, AD=3cm, angle ABC =135° and angle DAB =60° . Measure the size of angle BCD. (4 marks)
9. Given that OA=2i+3j and OB=3i-2j
   Find the magnitude of AB to one decimal place. (3 marks)
10. Given that tan x⁰=³/₇. Find cos (90-x)⁰ giving the answer of 4 significant figures.(2 marks)
11. Given that A=(¹_-2 ⁰₃).B=(³₂ ⁰₁) and C=2AB-A². Determine matrix C. (4 marks)
12. Without using mathematical tables or a calculator, solve the equation
    2log₁₀⁡x - 3log₁₀⁡2 + log₁₀⁡32 = 2 (3 marks)
13. A line L passes through point (3,1) and is perpendicular to line 2y=4x+5 .Determine the equation of line L. (3 marks)
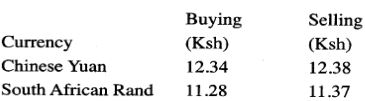
14. A forex Bureau in Kenya buys and sells foreign currencies as shown below:
    
    A businesswoman from china converted 195250 Chinese Yuan into Kenya Shillings.
    1. Calculate the amount of money ,in Kenya shillings ,that she received (1 mark)
    2. While in Kenya ,the businesswoman spent Ksh 125800 and then converted the balance into South African Rand .Calculate the amount of money , to the nearest rand ,that she received. (3 marks)
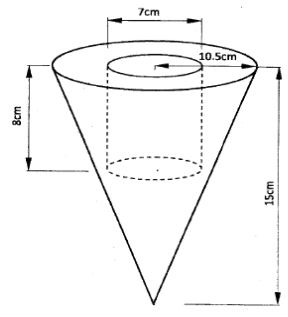
15. The figure below represents a solid cone with a cylindrical hole drilled into it . The radius of the cone is 10.5 cm and its vertical height is 15 cm. The hole has a diameter of 7 cm and depth of 8 cm.
    
    Calculate the volume of the solid. ( 3 marks )
16. Bukra had two bags A and B , containing sugar. If he removed 2kg of sugar from bag A and added it to bag B , the mass of sugar in bag B would be four times the mass of the sugar in bag A. If he added 10 kg of sugar to the original amount of sugar in each bag. The mass of sugar in bag B would be twice the mass of sugar in bag A .Calculate the original mass of sugar in each bag. (3 marks)
    

    SECTION II( 50 marks)
    Answer only five questions in this section in the spaces provided.

17. The table below shows the height, measured to the nearest cm, of 101 pawpaw trees.
    
    
    1. State the modal class (1 mark)
    2. Calculate to 2 decimal places:
       1. The mean height (4 marks)
       2. The difference between median height and the mean height. (5 marks)
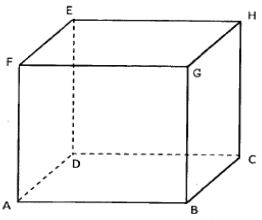
18. The figure below represents a solid cuboid ABCDEFGH with a rectangular base.
    AC =13 cm, BC =5 cm and CH =15 cm.
    
    
    1. Determine the length of AB. ( 1 mark)
    2. Calculate the surface area of the cuboid .( 3 marks)
    3. Given that the density of the material used to make the cuboid is 7.6g/cm³. calculate its mass in kilograms. ( 4 marks)
    4. Determine the number of such cuboids that can fit exactly in a container measuring 1.5m by 1.2 m by 1 m (2 marks)
19. Two alloys, A and B , are each made up copper ,Zinc and tin . In alloy A, the ratio of copper to Zinc is 3:2 and ratio of Zinc to tin 3:5.
    
    1. Determine the ratio , copper :zinc , alloy A. (2 marks)
    2. The mass of alloy A is 250 kg.Alloy B has the same mass as alloy A but the amount of copper is 30% less than alloy A.
       Calculate:
       1. The mass of tin alloy A ; (2 Marks)
       2. The total mass of zinc and tin in alloy B;(3 marks)
    3. Given that the ratio of zinc to tin in alloy B is 3:8 .determine the amount of tin in alloy B than in alloy A. (3 marks)
20. 1. Express  in the form ax²+bx+c=0, Where a,b and c are constants hence solve for x. ( 4 marks)
    2. Neema did y tests and scored a total of 120 marks. She did two more tests which she scored 14 and 13 marks. The mean score of the first y tests was 3 marks more than the mean score for all the tests she did. Find the total number of tests that she did. (6 marks)
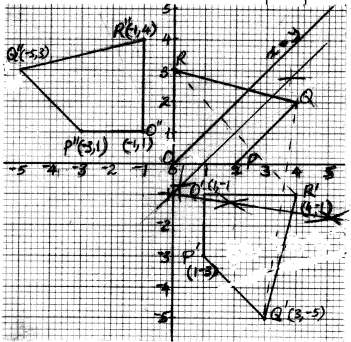
21. The vertices of quadrilateral OPQR are O(0,0),p(2,0), Q( 4,2) and R (0.3).the vertices of its image under a rotation are O’(I,-I),P’(1,-3),Q’(3,-5) and R’(4,-1).
    
    1. 1. On the grid provided, draw OPQR and its image O’P’Q’R’. (2 marks)
       2. By construction , determine the center and angle of rotation .(3 marks )
    2. On the same grid as (a)(i) above draw O’’P’’Q’’R’’, the image of O’P’Q’R’ under a reflection in the line y = x. (2 marks)
    3. From the quadrilaterals drawn , state the pairs that are:
       1. Directly congruent: (1 mark)
       2. Oppositely congruent.(2 marks)
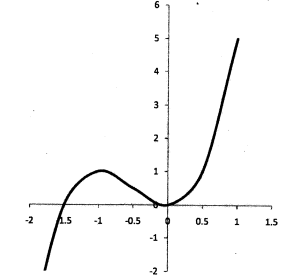
22. The equation of a curve is y = 2x³ +3x²
    
    1. Find :
       1. The x- intercept of the curve; (2 marks)
       2. The y- intercept of the curve .(1 mark)
    2. 1. Determine the stationary points of the curve. (3 marks)
       2. For each point in (b) (i) above , determine whether it is a maximum or a minimum. (2 marks)
    3. Sketch the curve. (2 marks)
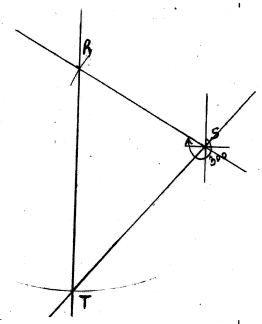
23. Three pegs R,S and T are on the vertices of a triangular plain field . R is 300 m from S on a bearing of 300⁰ and T is 450 m directly from south of R,
    1. Using a scale of 1cm to represent 60 m ,draw a diagram to show the positions of the pegs.(3 marks)
    2. Use the scale drawing to determine ;
       1. The distance between T and S in meters; (2 marks)
       2. The bearing of T from S .( 1 mark)
    3. Find the area of the field, in hectares, correct to one decimal place , ( 4 marks)
24. In the figure below PQ is parallel to RS. The Lines PS and RS intersect at T. RQ=10cm, RT:TQ=3:2, angle PQT =40° and angle RTS=80⁰.
    
    
    
    1. Find the length of RT. (2 marks)
    2. Determine, correct to 2 significant figures
       1. The perpendicular distance between PQ and RS; (2 mark)
       2. The length of TS.(2 marks)
    3. Using the cosine rule , find the length of RS correct to 2 significant figures, (2 marks)
    4. Calculate, correct to one decimal place, the area of triangle RST,(2 marks)

MARKING SCHEME 

1.  
   
   = ¹⁶/₁₅ − ¹⁴/₁₅
   = ²/₁₅ 
2.    1      = 4.630
   0.216
   √(0.512) = 0.8 × 4.630
     0.216
   = 3.704
3. (2x² − 3y³)² + 12x²y³
   =4x⁴ − 12x²y³ + 9y² + 12x²y³ 
   =4x⁴ + 9y⁶
4. ²⁴/₂ = ½ × 8 × x sin 30°
   x =     12      = 6cm
         4 sin 30
   perimeter = 2(6+8) = 28
5. 9^2y × 2^x = 9 × 8
   (3²)^2y × 2^x = 3² × 2³
   (3²)^2y = 3  and 2^x = 2³
   4y = 2 and x = 3
   y = ½ and x = 3
6. LCM of 9,15 and 21
   3² × 5 × 7 = 315 minutes
   last time of ringing together
   11:00
   −5:15
     5:45p.m
7. ^x/₈ = ^x/₂₀ + ¼
   ^x/₈ − ^x/₂₀ = ¼
   ⇒ ^3x/₄₀ = ¼
   x = 3¹/₃
   Distance to shoppinig centre
   12 − 3¹/₃ = 8²/₃km
8.  
   
   Construction of 135° angle between lines AB = 4cm and BC = 6cm 
   Construction of 60° angle between lines AB = 4cm and AD = 3cm 
   Completion of quadrilateral ABCD 
   ∠BCD = 31°± 1°
9.  
   
   magnitude = √(1²+ (−5)²
                   =√26 ≃ 5.1
10. x = tan^{−1   3}/₇ = 23.20°
    Cos(90 − 23.2)° = 0.3939
11.  
    
12. log =  = 2
    x² × 2⁵ = 100
    2³  
    4x² = 100
    x = √25 = ±5
    x = 5 
13. 2y = 4x + 5 ⇒ y = 2x + ⁵/₂
    gradient, M₁ of line = 2
    gradient, M₂, of perpendicular is given by 
    2M₂ = −1 ⇒ M₂ = −½
    equation of line L 
    y − 1 = −½
    x − 3
    y = −½x + ⁵/₂
14.  
    1. 195250 Chinese Yuan into Kenya shillings
       =195250 × 12.34 = 2409385
    2. Balance:
       =2409385 − 1258000
       = 1151385
       Balance in S. A Rand
       =1151385
            11.37
       =101265
15. Volume of solid
    = ¹/₃ × ²²/₇ × 10.5² × 15 − ²²/₇ × 3.5² × 8
    =1732.5 − 308
    =1424.5cm³
16. 4(A − 2) = B + 2
    2(A+10) = B + 10
    4A − B = 10 ........(i)
    ±2A ± B = ±10....(ii)
              2A = 20
    ⇒ A = 10
    Substitute A = 10 in (i)
    4 × 10 − B = 10
    ⇒ B = 30
17.  
    1. modal class 40-44
    2.  
       1. mid points:
          22, 27, 32, 37, 42, 47, 52, 57
          22 × 2 +27 × 15 + 32 × 18 + 37 × 25 + 42 × 30 + 47 × 6 + 52 × 3 + 57 × 2  = 37.25
                                                                 101
       2. Cumulativce frequencies
          2, 17, 35, 60, 90, 96, 99, 101
          ¹⁶/₂₅ × 5 = 3.2
          34.5+3.2 = 37.7
          difference 37.7 − 37.25
                        =0.45
18.  
    1. /AB/ = √(169 − 25) = 12
    2. 2 × 5 × 12 + 2 × 5 × 15 + 2 × 12 × 15
       =630cm²
    3. Volume = 5 × 12 × 15cm³ 
       mass = 7.6 × 5 × 12 × 15
               = 6840gm
               = 6840 
                  1000
               = 6.84kg
    4. 150 × 120 × 100cm³
           15 × 12 × 5cm³  
       = 2000
19.  
    1. Ratio : Copper : zinc : tin
       copper  zinc   tin
        3          2      5
                    3
        9          6      10
       Copper : zinc : tin = 9 : 6 :10
    2.  
       1. mass of tin 
          = 250 × ¹⁰/₂₅
          =100kg
       2. mass of zinc and tin in alloy B:
          mass of copper = ⁷⁰/₁₀₀ × 90 
                                 =63
          ∴ mass of zinc and tin: 
          = 250 − 63
          =187
    3. amount of tin in alloy A than B
       mass of tini in alloy B 
       = ⁸/₁₁ × 187
       = 136
       diffrence:
       136 − 100
       =36
20.  
    1.   1   −  2    =  3  
       x−2    x+5    x+1
       x+5−2(x−2) =   3  
        (x−2)(x+5      x+1
           −x+9       =   3  
       x² +3x−10       x+1
       4x² + x − 39 = 0
       (4x+13)(x−3)=0
       x = 3 or x = −3¼
    2. mean for second set of tests
       =  147
           y+2
       120 − 147 = 3
         y      y+2
       120y+240−147y = 3
               y(y+2)
       −27y+240=3y²+6y
       −9y+80=y²+2y
       y²+11y−80=0
       (y−5)(y+16)=0
       y=5 or −16
       No. of tests: 5+2=7
21.   
       
    1.  
       1. OPQR ✓drawn
          O'P'Q'R' ✓drawn
       2. Perpendicular bisectors ✓ drawn ( at least 2)
          centre of rotation (0, −1) shown
          angle of rotation −90° 
    2. line of reflection x = y drawn
       quadrilateral O''P''Q''R'' drawn
    3.  
       1. directly congruent quads:
          OPQR and O''P''Q''r''
       2. Oppositely congruent quads:
          OPQR and O''P''Q''R''
          O'P'Q'R' and O''P''Q''R''
22.   
    1.  
       1. x - intercepts 
          when y =0
          x²(2x+3) = 0
          x=0 and x =−³/₂
       2. y - intercept
          when x=0, y=0
    2.  
       1. stationary points of curve
          ^dy/_dx = 6x² + 6x 
          stationary points when dy = 0
                                            dx
          i.e 6x² + 6x = 0
          6x(x+1) =0
          x=0 or x=−1
          ∴ stationary points are:
          (0,0) and (−1,1)
       2.  
          

          x	−2	−1½	−1	−½	0	½	1
          dy/dx	12	4½	0	−1½	0	4½	12

          minimum point (0,0)
          maximum point (−1,1)
    3.  
       
       points plotted at (−1½, 0), (−1,1) and (0,0)
       smooth curve
23.  
    1.  
       
       ✓ location of R   length 5 cm and bearing 300°
       ✓location of t    length 7.5cm; south of R
       complete ∆
       
    2.   
       1. Distance TS: 6.6(±.1)cm
          conversion 6.6 × 60 = 396m
       2. Bearing of T from S
          180 + 41°(±1°) = 221°
    3. area of field
       ∠TRS = 60°
       area = ½ × 300 × 450 sin 60°
       =58456.71476
              10000
       =5.8ha
24.  
    1. length of RT:
       = ³/₅ × 10
       =6cm
    2.  
       1. Perpendicular diatnace between PQ and RS 
          =10 sin 40
          =6.4cm
       2.   TS   =    6    
          sin 40   sin 60
          TS = 6×sin40
                    sin60
               =4.5cm
    3. length  RS using cosine rule
       RS² = 6² + 4.5² − 2 × 4.5 × 6 cos 80
       =46.87299841
       RS=6.85
    4. area of ∆ RST 
       =½ × 6 × 4.5 sin 80
       =13.3