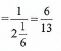KCSE 2018 Mathematics Alternative B Paper 1 with Marking Scheme

QUESTIONS

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided

1. The sum of 3 133 792, 5293 476, 7672 598 and 4257 348 is rounded off to the nearest 10000. Find the difference between the actual sum and the rounded figure.(3 marks)
2. Express 1 728 as a product of its prime factors, hence find the cube root of 1728.(3 marks)
3. Ngata's office is on the twenty second floor in a storey building. On a certain day, he walked up five floors from his office to another office. He then took a lift to the third floor. Calculate the number of floors he went through while in the lift.(2 marks)
4. Given that 2^2x = 1024, find 3^x. (3 marks)
5. A metal dealer had a piece of wire which he intended to cut into pieces of 8m, 15 m or 21 m. Determine the minimum length of the wire that would give an exact number of pieces of each length.(3 marks)
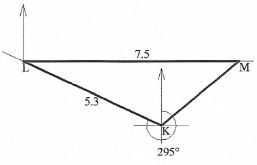
6. Three villages K, L and M are such that L is 53 km from K on a bearing of 295º Village M is 75km east of village L.
   1. Using a scale of 1 cm to represent 10km, draw a diagram to show the positions of villages K, L, and M.(2 marks)
   2. Use the scale drawing to determine the bearing and distance of village M from K.(2 marks)
7. Use factor method to solve:(3 marks)
   2^x2 = 3x +9
8. A straight line L passes through (-3,5) and is perpendicular to 2x + 3y = 6. Find the equation of line L, in the form ay + bx = c. (3 marks)
9. Waswa boarded a bus that took off at 9.45 pm on a Sunday to visit his sister in Nairobi, The bus took 8 hours 20 minutes to arrive in Nairobi. After 10 minutes, he took a taxi that took 42 minutes to arrive at his sister's home. Find the day and time, in 24 hour system, when Waswa arrived at his sister's home. (3 marks)
10. Simplify the expression: (3 marks)
    
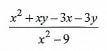
11. A cone of height of 8 cm has a slant length of 10 cm. Calculate the volume of the cone. (Take π = 3.142) (3 marks)
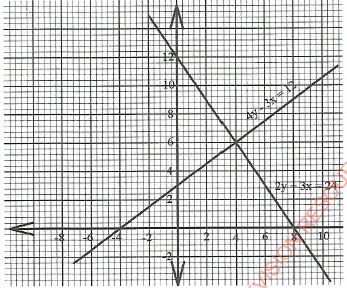
12. Use the grid provided below to solve the equations:
    4y - 3x = 12
    2y + 3x = 24.                (4 marks)
13. Given that θ = 2, find tan θ correct to 2 decimal places. (2 marks)
                          3
14. A cylindrical container of diameter 28 cm and height 45cm is filled with milk. If the mass of the milk is 26.61 kg, calculate the density of the milk in g/cm³, correct to 2 decimal places. (3 mark)
15. Kantai had Ksh 81 000 which he changed to dollars at the rate of Ksh 101.25 per dollar. He later sold the dollars to a bank which bought 1 dollar for Ksh 102.56. Calculate the money gained in Kenya shillings. (4 marks)
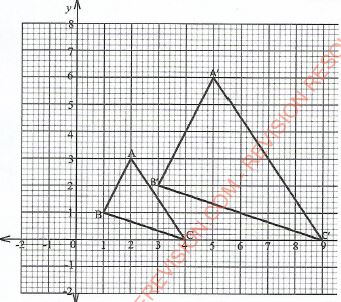
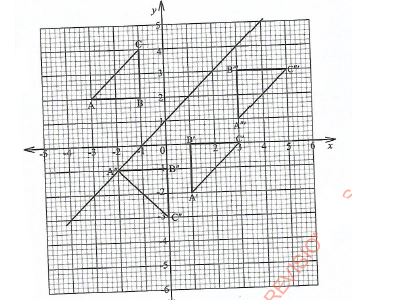
16. A triangle ABC with vertices A(2,3), B(1,1) and C(4.0) is mapped onto triangle ABC by an enlargement scale factor 2, centre (-1,0).
    On the grid provided, draw:
    1. triangle ABC; (1 mark)
    2. triangle A'B'C'. (3 marks)

SECTION II (50 marks)
Answer any five questions in this section in the spaces provided.

17. The Hire Purchase (H.P.) price of a sofa set was Ksh 54000. A discount of 20% was allowed on the H.P. price if one bought it by cash.
    1. Calculate the cash price.(2 marks) 
    2. Mugure bought the sofa set on H.P. terms and paid 10% of the H.P. price as deposit
       She paid the remainder in 18 equal monthly instalments.
       1. Calculate the amount paid as deposit.(2 marks)
       2. Calculate the monthly instalments.(2 marks) 
    3. Karigo bought an identical sofa set as Mugure. She opted for a longer repayment period than Mugure and paid a 10% deposit and a monthly instalment of Ksh 2268. If the total H.P. price paid by Karigo was 12% more than that paid by Mugure, calculate Karigo's repayment period.(4 marks)
18. Mary can complete a task in 2 hours 10 minutes while Jane can complete the same task in 2 hours.
    1. Determine the time both Mary and Jane would take to complete the task if they work together.(4 marks)
    2. Mary and Jane embarked on the task and worked together for 30 minutes. They were then joined by Rachel and the three completed the remaining task in 20 minutes,
       1. Find the proportion of work that was remaining before Rachel joined in.(2 marks)
       2. Calculate the fraction of work done by Rachel in the 20 minutes. (4 marks)
19. A rectangular plot of land measures (3x+9) m by (x-3) m and has an area of 648 m².
    1. Write an equation for the area of the plot in the form, ax² +bx+c = 0.(2 marks)
    2. Determine the dimensions of the plot.(4 marks)
    3. Another similar plot has an area of 2592m² Find the dimensions of this plot.(4 marks)
20. In the figure below A,B,C and D are points on the circumference of the circle centre O. Line TDF is a tangent to the circle at D and AB produced meets the tangent at T. ∠ACD = 34º and ∠BAC = 25°
    
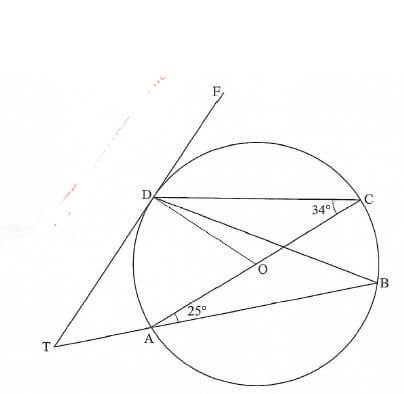
    Giving reasons in each case, find the size of:
    1. ∠AOD(2 marks)
    2. ∠BDC(2 marks)
    3. ∠ACB(2 marks)
    4. ∠FDC(2 marks)
    5. ∠ATD(2 marks)
21. The vertices of a triangle ABC are A(-3,2), B(-1,2) and C(-1,4).
    1. On the grid provided, draw triangle ABC.  (1 mark)
    2. Triangle ABC is reflected on line y=x+1.
       1. Draw line y=x+1.(2 marks)
       2. Draw triangle A'B'C', the image of triangle ABC under reflection in the line y=x+1.(2 marks)
    3. Draw triangle A"B"C", the image of triangle A'B'C' under a rotation of -90° about (0,0).(2 marks)
    4. Under a translation 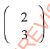, triangle A'B'C' is mapped onto A"B"C".
       1. Find the coordinates of A"B"C".(2 marks)
    5. Draw triangle A"B"C".(1 mark)
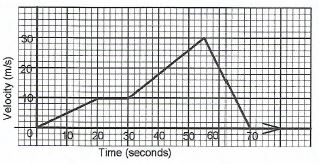
22. A car started from rest and moved at a constant acceleration of 0.5 m/s2 for 20 seconds. It maintained a constant velocity for the next 10 seconds before accelerating at 0.8 m/s2 for 25 seconds. It then decelerated uniformly and came to rest after 15 seconds.
    1. On the grid provided, draw the velocity-time graph for the car.(4 marks)
    2. Use the graph to determine:
       1. the deceleration of the car;(2 marks)
       2. the total distance covered by the car,(2 marks) 
       3. the average speed of the car, correct to 2 decimal places. (2 marks)
23. The figure below represents a wooden model. The model consist of a frustrum part and a cylindrical part. The diameter of the cylindrical part is 18 cm and the height is 30cm. The height of the frustrum part is 80 cm.
    
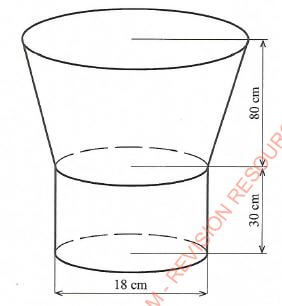
    If the vertical height of the cone from which the frustum was cut was 120 cm, calculate:
    1. the larger radius of the frustrum;(2 marks)
    2. the slant height of the frustrum;(4 marks)
    3. the surface area of the model.(4 marks)
24. A cylindrical container of radius 14 cm has a capacity of 12.32 litres. (Take π = ²²/₇)
    1. Calculate the height of the container.(3 marks)
    2. The container was used to store juice. If the container was full of juice and some of it was used up to a level of 5 cm, calculate the amount, in litres, of juice used.(3 marks)
    3. The remaining juice was packed into cylindrical bottles of radius 2 cm and height 8.4 cm. Calculate the number of bottles of juice obtained.(4 marks)

MARKING SCHEME

1. 3133792 +5293476 + 7672598 +4257348 = 20357214
   To the nearest 10000
   = 20360000
   Difference = 20 360 000 - 20 357 214
   = 2786
2. 1728 = 2⁶ × 3^{3
   3}√1728 = ³√2⁶ × 3³
   = 2² × 3
    =12
3. 22+5-n=3
   n=27-3
   = 24
   Number of floors while in lift = 24
4. 2^2x = 2¹⁰
   2x=10
   x = 5
   therefore: 3⁵ = 243
5. 8= 2x2x2
   15= 3x5
   21=3x7
   L.C.M = 2³x5x7x3
   = 840
6.                    
   1.                                  
      
   2. Bearing of M from K=050°
      Distance of M from K= 35 km
7. 2x²-3x-9=0
   2x² - 6x+3x-9=0
   2x(x-3)+3(x-3)=0
   (x-3)(2x+3)=0
   x = 3 or x=-1.5
8. Gradient of 2x+3y=6
   is -2
       3
   Gradient of L = 3
                          2
   y - 5  = 3
   x + 3    2
   3x+9=2y-10
   3x-2y=-19
9. Time the journey took
   8hrs 20min + 10min + 42min = 9hrs 12 min
   Time of arrival
   = 9.45p.m. + 9hrs 12min - 12hrs
   = 06.57am
   Day and Time of arrival
   Monday at 0657h
10. x² + xy-3x-3y
     (x-3)(x+3)
    = x(x+y)-3(x+y)
           (x-3)(x+3)
    = (x + y)(x-3)
       (x-3)(x+3)
    = x+y
       x+3
11. Radius of cone = √10² - 8² = 6
    Volume = ¹/₃ x 3.142x 6² x 8
    = 301.632cm³
12.                                
    
    x = 4   y = 6
13. Cos θ = ²/₃
    θ = cos-^1 2/₃
    = 48.19°
    Tan θ = 1.12
14. Vol = ²²/₇ x 14 x 14 x 45
    = 27720cm³
    Density = 26.61x1000
                       27720
    = 0.96g/cm³
15. Amount in dollars
    = 81000
       101.25
    = 800 Dollars
    Amount gained
    =800 x 102.56 - 81000
    =Ksh 1048
16.                    
                      
    1. ΔABC correctly drawn
    2. Location of A'(5,6),B'(3.2) and C'(0,0)
       Drawing ΔABC
17.                  
    1. Cash price = 80 x 54000
                          100
       = Ksh 43 200
    2.                        
       1. 10 x 54000
          100
          = Ksh 5 400
       2. Monthly installment
          = 54000-5400
                   18
          =Ksh 2 700
    3. H.P price for Karigo
       = 1.12 x 54 000 
       = Ksh 60 480
       Deposit = 10 x 60480
                     100 
       = Ksh 6048
       No. of months
       = 60480–6048
               2268 
       = 24 months
18.                  
    1. Fraction of work Mary can do in 1 hr= 
       Fraction of work Jane can do in 1 hr = ¹/₂
       Fraction of work done by Mary and Jane in 1 hr = 1 + 6 = 25
                                                                               2   13    26
       Time taken to complete = 1 ÷  25
                                                    26
       =1.04hrs
    2.                          
       1. Fraction of work done by Mary and Jane in 30 min
          = 25 x 1 
             26    2
          = 25
             52
          Remaining portion = 1 - 25 = 27
                                             52     52
       2. Fraction of work done by Mary and Jane in 20 minutes
          =  25 x 1
              26    3
          = 25
             78
          Fraction of work done by Rachel
          = 25  + x = 27
             78            52
          x = 27  -  25
                52     78
          = 31
            156
19.                        
    1. (3x +9)(x-3) = 3x² +9x-9x-27
       3x²-27=648
       therefore: 3x² -675=0
    2. 3x²-675 = 0
       x²-225 = 0
       (x+15)(x-15)=0
       x = 15m
       Length of plot=3x15 + 9 = 54m
       Width of plot=15 - 3 = 12m
    3. A.S.F. = 2592
                    648
       L.S.F. = √4 = 2
       Length of similar plot = 54 x 2 = 108m
       Width of similar plot = 12 x 2 = 24m
20.                          
    1. ∠AOD=2 x 34°= 68°
       Angle subtended at centre by arc AD = 2 x angle subtended at circumference
    2. ∠BDC = ∠BAC = 25°
       Angle subtended by same chord at the circumference
    3. ∠ACB= 90 - 25°= 65°
       Angle sum of triangle.
       ∠ABC = 90° (angle subtended by diameter to the circumference)
    4. ∠FDC = 90 - 34° = 56°
       ∠ODF-90° angle made by tangent and radius and ΔODC is isosceles
    5. ∠ATD=360°-(155+90 +68)
       = 47°
       Angle sum in quadrilateral AODT 
21.                                    
                                    
    1. Δ ABC correctly drawn
    2.                      
       1. Line y=x+1
       2. Plotting of points A'B' and C'
          Δ A'B'C' correctly drawn
    3. Points A", B' and C" plotted ΔA'B'C' correctly drawn
    4.                          
       1. 
       2. ΔA''B''C'' correctly drawn
22.                            
              
    1. Scale
       Acceleration parts
       Constant speed
       Deceleration
    2. Deceleration = 30
                             15
       = 2m/s²
    3. Total distance covered 
       = ¹/₂x10x20+10x10+ ¹/₂(10+30)x 25+¹/₂ x15x30
       = 100+ 100+ 500+225
       =925m
    4. Average speed
       = 925
            70
       = 13.21m/s
23.                          
    1. 120 = r
        40     9
       r=27
    2. Slant height of larger cone
       = √27² +120²
       = 123
       Slant height of smaller conc
       = √40² +9² 
       = 41
       Slant height of cone
       = 123-41
       = 82 cm
    3. Surface Area of model
       
24.                    
    1. Height of container
       22x14x14xh = 12.32 x 1000cm³
       7
       h = 12320x7
             22x14x14
       =  20cm
    2. Amount of juice used
       22x15x14x14
       7
       =9240cm³
       In litres = 9240
                      1000
       =9.24 litres
    3. Vol of bottle
       = 22x2x2x8.4
          7
       = 105.6cm³
       Remaining juice
       = 12.320 - 9.24
       = 3.08 litres
       No. of bottles packed
       =   3.08  = 29.16
          0.1056
       = 29 bottles