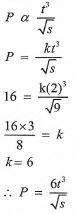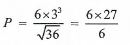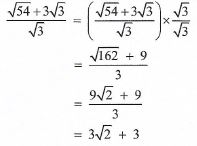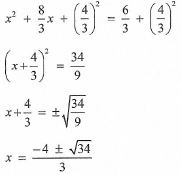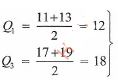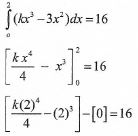KCSE 2018 Mathematics Alternative A Paper 2 with Marking Scheme

Share via Whatsapp

« Previous Topic
KCSE 2018 Mathematics Alternative A Paper 1 with Marking Scheme

Next Topic »
KCSE 2018 Mathematics Alternative B Paper 1 with Marking Scheme

Download PDF for future reference Get on Whatsapp for 50/-

QUESTIONS

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

Given that 2 log x² + log √x = k log x, find the value of k.(2 marks)
A variable P varies directly as t³ and inversely as the square root of s. When t=2 and s=9, P=16. Determine the equation connecting P, t and s, hence find P when s = 36 and 1 = 3. (4 marks)
Asia invested some money in a financial institution. The financial institution offered 6% per annum compound interest in the first year and 7% per annum in the second year. At the end of the second year, Asia had Ksh 170130 in the financial institution. Determine the amount of money Asia invested.(3 marks)
The figure below represents a wedge ABCDEF. EF = 10 cm, angle FBE = 45° and the angle between the planes ABFE and ABCD is 20º.

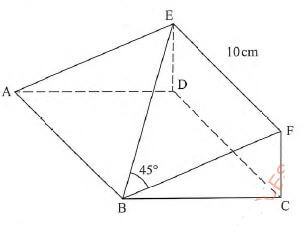
Calculate length BC, correct to 1 decimal place. (3 marks)
Simplify
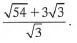(2 marks)
In the figure below, AB is a tangent to the circle, centre an angle of 6cm. The arc AC substends an angle of 60º at the centre of the circle.

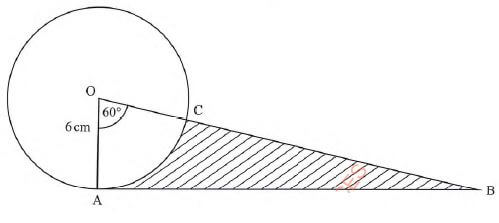
Calculate the area of the shaded region, correct to 1 decimal place. (4 marks)
Use completing the square method to solve 3x² + 8x - 6 = 0, correct to 3 significant figures. (3 marks)
Three workers, working 8 hours per day can complete a task in 5 days. Each worker is paid Ksh 40 per hour. Calculate the cost of hiring 5 workers if they work for 6 hours per day to complete the same task.(3 marks)
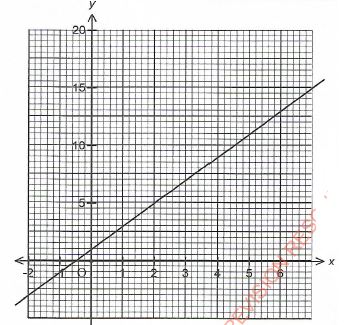
The table below represents a relationship between two variables x and y.

x 1 2 3 4 5 6

y 3.5 4.5 8.0 8.5 11 13
1. On the grid provided draw the line of best fit. (3 marks)
2. Use the graph to find the value of y when x= 0 (1 mark)
State the amplitude and the phase angle of the curve
y=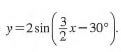 (2 marks)
The mass, in kilograms, of 9 sheep in a pen were: 13, 8, 16, 17, 19, 20, 15, 14 and 11. Determine the quartile deviation of the data. (3 marks)
The position of two points C and D on the earth's surface are (θ°N, 10°E) and (θ'N, 30°E) respectively. The distance between the two points is 600 nm. Determine the latitude on which C and D lie. (3 marks)
In the figure below OP=p, OR = r, PQ:QR = 1:2 and PS = 3PR.

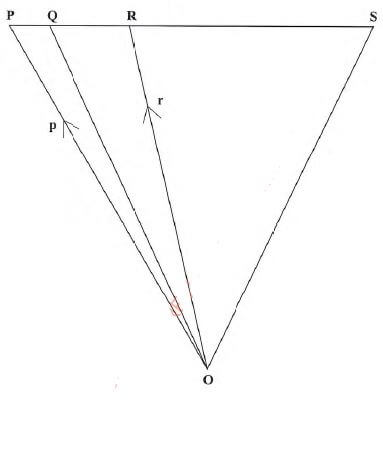
Express QS in terms of p and r. (4 marks)
In a certain firm there are 6 men and 4 women employees. Two employees are chosen at random to attend a seminar. Determine the probability that a man and a woman are chosen. (3 marks)
Under a transformation T= 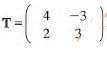triangle OAB is mapped onto triangle OA'B' with 23 vertices 0(0,0), A' (18,0) and B (18,6). Find the area of triangle OAB. (3 marks)
Find the value of k if 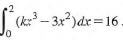(4 marks)

SECTION II (50 marks)
Answer any five questions from this section in the spaces provided.

The 5th and 10th terms of an arithmetic progression are 18 and -2 respectively
1. Find the common difference and the first term.(4 marks)
2. Determine the least number of terms which must be added together so that the sum of the progression is negative. Hence find the sum.(6 marks)
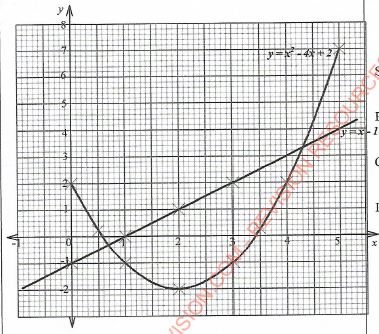
1. Complete the table below for the equation y = x2 - 4x + 2 (2 marks)
  
  x 0 1 2 3 4 5
  
  y
2. On the grid provided draw the graph 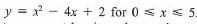. Use 2cm to represent I unit on the x-axis and 1 cm to represent 1 unit on the y-axis. (3 marks)
3. Use the graph to solve the equation,
  x² - 4x + 2 = 0 (2 marks)
4. By drawing a suitable line, use the graph in (b) to solve the equation
  x² - 5x + 3 = 0 (3 marks)
1. The table below shows the frequency distribution of heights of 40 plants in a tree nursery.
  
  heights of plants (cm) 0-10 10-20 20-30 30-40 40-50 50-60
  
  frequency 4 8 10 12 4 2
  
  State the modal class. (1 mark)
2. Calculate:
  1. the mean height of the plants; (3 marks)
  2. the standard deviation of the distribution.(4 marks)
3. Determine the probability that a plant taken at random has a height greater than 40 cm.(2 marks)
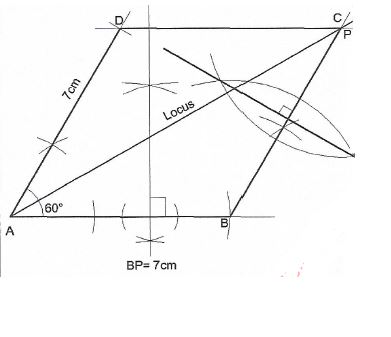
1. Using a ruler and a pair of compasses only, construct:
  1. a parallelogram ABCD, with line AB below as part of it, such that AD = ? cm and angle BAD = 60°; (3 marks)
  2. the locus of points equidistant from AB and AD; (1 mark)
  3. the perpendicular bisector of BC. (1 mark)
2. 1. Mark the point that lies on DC and is equidistant from AB and AD. (1 mark)
  2. Measure BP. (1 mark)
3. Describe the locus that the perpendicular bisector of BC represents. (1 mark)
4. Calculate the area of trapezium ABCP. (2 marks)

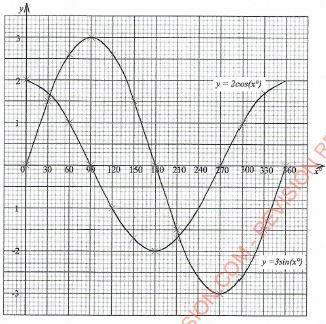
The table below shows some values of the curves y = 2 cos x and y = 3 sin x.

Complete the table for values of y = 2 cos x and y = 3 sin x, correct to 1 decimal place. (2 marks)

x°	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°	360°
y=2cosx	2		1	0		-1.7		-1.7	-1		1	1.7	2
y=3sinx	0	1.5		3	2.6		0		-2.6			-1.5	0

On the grid provided, draw the graphs of y = 2 cos x and y , on the same axes. (5 marks)
Use the graph to find the values of x when 2 cos x - 3 sin x = 0 (2 marks)
Use the graph to find the values of y when 2 cos x= 3 sin x. (1 marks)

The figure below is a model of a watch tower with a square base of side 10cm. Height PU is 15 cm and slanting edges UV = TV = SV = RV = 13 cm.

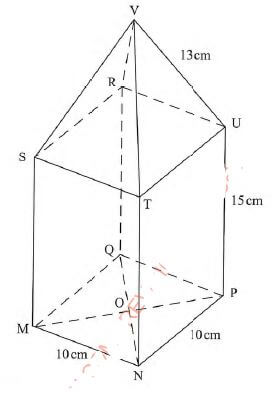
Giving the answer correct to two decimal places, calculate:
1. length MP;(2 marks)
2. the angle between MU and plane MNPQ;(2 marks)
3. Length VO;(3 marks)
4. the angle between planes VST and RSTU.(3 marks)
The table below shows monthly income tax rates for a certain year.

monthly income (in ksh) tax rate in each shilling

0-11 180 10%

11 181-21 714 15%

21 715-32 248 20%

32 249-42 782 25%

above 42 782 30%

In that year a monthly personal tax relief of Ksh 1280 was allowed. In a certain month of that year, Sila earned a monthly basic salary of Ksh 52 000, a house allowance of Ksh 7800 and a commuter allowance of Ksh 5000.
1. Calculate:
  1. Sila's taxable income,(2 marks)
  2. the net tax payable by Sila in that month;(5 marks)
2. In July that year, Sila's basic salary was raised by 4%. Determine Sila's net salary in July(3 marks)
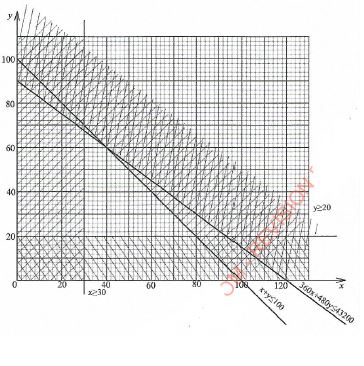
A hotel buys beef and mutton daily. The amount of beef bought must be at least 30kg and that of mutton at least 20 kg. The total mass of beef and mutton bought should not exceed 100 kg. The beef is bought at Ksh 360 per kg and the mutton at Ksh 480 per kg. The amount of money spent on both beef and mutton should not exceed Ksh 43 200 per day. Let x represent the number of kilograms of beef and y the number of kilograms of mutton.
1. Write the inequalities that represent the above information(3 marks)
2. On the grid provided, draw the inequalities in (a) above.(4 marks)
3. The hotel makes a profit of Ksh 50 on each kg of beef and Ksh 60 on each kg of mutton. Determine the maximum profit the hotel can make. (3 marks)
Desert kangaroo rats spend most of their time in underground burrows.
1. Name this type of behavioural activity(1 mark)
2. Explain the significance of this behaviour to the organism.(3 marks)
State two advantages terrestrial animals have in excreting urea as their main nitrogenous waste product.(2 marks)
Below is a graphical representation of how basal metabolic rates compare in various animals.

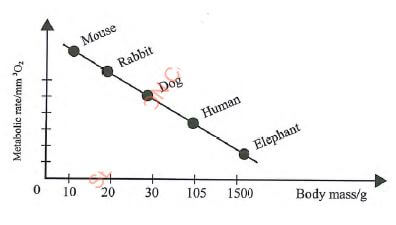
From the graph, explain why the mouse has a higher breathing rate than the elephant. (3 marks)

MARKING SCHEME

2 log x² + log√x = k log x
log (x⁴x^1/2) = log x^kk = 4¹/₂
When t = 3 and s = 36

= 27
P₂(1.07) = 170130
P₂ = 170130
1.07
= 159000
P₁ = 159000
1.06
= Ksh 150000
BF = 10
Cos 20° = BC
10
BC = 10 Cos 20°
= 9.4 cm
AB = 6 tan 60° or OB = 6
cos 69
Area of triangle OAB = ¹/₂ x 6 x 6 tan 60°
Area of sector OAC = 60 x π x 6²
360
Area of shaded part = 31.18 -18.85
= 12.3 cm²
3x² + 8x = 6

x = -3.28 or x = 0.610
W:H:D
3: 5:5
5: 6:x
No. of days = 5 x 8 x 3
6 5
= 4 days
Cost = 5 x 6 x 4 x 40
= Ksh 4800
2. When x = 0, y=1
Amplitude = 2
Phase angle = 30°
8, 11, 13, 14, 15, 16, 17, 19, 20

Quartile deviation = ¹/₂(18-12)
= 3
Longitude difference = 30 - 10 = 20°
600 = 20 x 60 Cos θ
Cos θ = 0.5
θ = 60°
Latitude = 60°N
OQ = 2P + 1r
3 3
OS = p+3(r - p)
= 3r - 2P
QS = -OQ + OS
= -2P - 1r + 3r - 2p
3 3
= 8r - 8p
3 3
P (MW or WM) = 6 x 4 + 4 x 6
10 9 10 9
= 24 + 24
90 90
= 8
15
Det (T) = 18
Area of object OAB = Area of image
Det(T)
= 1/2 x 18 x 16
18
= 3 units
4k - 8 = 16
4k = 24
k = 6
1. a + 4d = 18 (i)
  a + 9d = -2 (ii)
  5d = -20
  d = -4
  a = 34
2. ⁿ/₂{2 x 34 + (n-1)(-4)} = 0
  ⁿ/₂{72 - 4n} = 0
  4n = 72
  n = 18
  least number of terms=19
  S₁₉ = ¹⁹/₂ {2 x 34+18(-4)}
  = ¹⁹/₂(68 - 72)
  = ¹⁹/₂(-4)
  = -38
1. x 0 1 2 3 4 5
  
  y = x² - 4x + 2 2 -1 -2 -1 2 7
3. x=0.6 ± 0.05
  x=3.4 ± 0.05
4. y = x² - 4x + 2
  - 0 = x²- 5x + 3
  y = x - 1
  when y = x - 1, then
  x = 0.7 ± 0.05
  x = 4.3 ± 0.05
1. modal class 30-40
2. x f fx x² fx²
  
  5
  15
  25
  35
  45
  55 4
  8
  10
  12
  4
  2 20
  120
  250
  420
  180
  110 25
  225
  625
  1225
  2025
  3025 100
  1800
  6250
  14700
  8100
  6050
  
  40 1100 37000
  1. x = Σxf = 1100
    N 40
    = 27.5
  2. s.d² = 37000 – 27.5² 40
    = 925 - 756.25
    =168.75
    s.d = √168.75
    = 12.99
3. No of plants whose height > 40 = 4+2 = 6
  P(Height > 40cm) = 6 = 0.15
  40
1. 1. <BAD = 60°
    Line DC or BC correctly drawn
    Point C correctly located
    Parallelogram ABCD
  2. Angle bisector of <BAD
  3. bisector of BC drawn
2. 1. Point P identified and marked on line DC
  2. BP = 7 ± 0.1cm
3. Locus of points equidistant from B and C
1. x 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° 360°
  
  2cosx 1.7 -1 -2 0 1.7
  
  2.6 1.5 -1.5 -3 -2.6
3. 2cos x - 3sin x = 0
  = 2cosx = 3sinx
  x= 34° and x =214°
4. y = 1.6 and y = -1.6
1. Length of MP
  MP² =10² +10²
  MP = √200 = 14.14
2. Angle between MỤ and plane MNPQ
  tan θ₁ = 15
  √200
  θ₁ =tan^-1 ( 15 )
  ( √200 )
  = 46.69
3. Length VO
  h=Height of pyramid
  = √(13² -7.07²)
  = 10.91
  VO=15 + h = 15+ 10.91
  = 25.91
4. Angle between planes VST and RSTU
  cosθ₂ = 5
  12
  θ₂ =cos^-1 ( 5 )
  ( 12 )
  65.38°
1. Taxable income
  1. = 52000+ 7800 + 5000
    = Ksh 64800
  2. Tax payable
    11180x0.1=1118
    10534x0.15 = 1580.10
    10534x0.2 = 2106.80
    10534x0.25 = 2633.50
    22018x0.3 =6605.4
    Total tax = 14043.8
    Net tax = 14043.8-1280
    = 12763.8
2. Additional tax
  = 4 x 52000 x 0.3
  100
  = Ksh 624
  Net salary = 64800 - 12763.8 - 624 + ( 4 x 52 000)
  100
  =Ksh 53492.20
1. x>30 ; y≥20
  x+y≤100
  360x+480y≤43200 or 3x+4y≤360
3. Objective function = 50x+60y
  Profit = 50 x 40+ 60 x 60
  = 5600