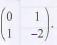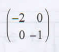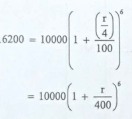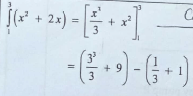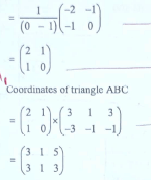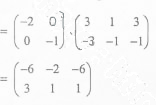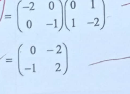Mathematics Paper 2 Questions and Answers - KCSE 2021 Past Papers

SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.

1. An empty tank of capacity 18480 litres is to be filled with water using a cylindrical pipe of diameter 0.028 m. The rate of flow of water from the pipe is 2 m/s. Find the time in hours it would take to fill up the tank. (Take π = ²²/₇). (3 marks)
2. The first term of a Geometric Progression (G.P) is 2. The common ratio of the G.P is also 2. The product of the last two terms of the G.P is 512. Determine the number of terms in the G.P. (3 marks)
3. The expression ax² - 30x + 9 is a perfect square, where a is a constant. Find the value of a. (2 marks)
4. Make x the subject of the formula y =    bx      (3 marks)
                                                             √cx² - a  
5. The figure below shows a circle and a point outside the circle
   
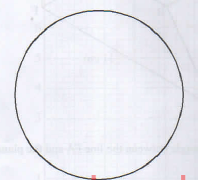
   Using a ruler and pair of compasses, construct a tangent to the circle from P. (4 marks)
6. Four quantities P Q R and Sare such that P varies directly as the square root of Q and inversely as the square of the difference of R and S. Quantity Q is increased by 44% while quantities R and Sare each decreased by 10%.
   Find the corresponding percentage change in P correct to 1 decimal place. (4 marks)
7. The figure below represents a prism ABCDEFGH of length 6 cm. The cross section BCFG of the prism is a trapezium in which GF = 11 cm, BC = 8 cm, BG = 5 cm and ∠GFC = ∠BCF = 90°
   
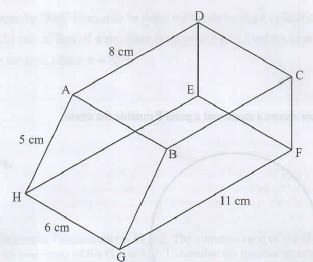
   Calculate correct to 1 decimal place the angle between the line FA and the plane GFEH. (3 marks)
8. The cash price of a gas cooker is Ksh 20 000. A customer bought the cooker on hire purchase terms by paying a deposit of Ksh 10 000 followed by 18 equal monthly instalments of Ksh 900 each, Annual interest, compounded quarterly, was charged on the balance for the period of 18 months. Determinc, correct to 1 dccimal place, the rate of intcrcst per annum. (4 marks)
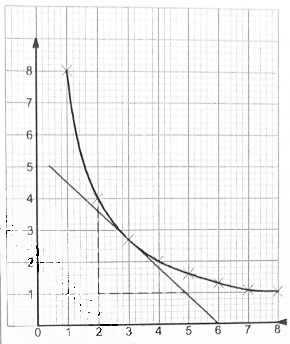
9. The table below shows the values oft and the corresponding values of h for a given relation
   

   t	1	2	3	4	5	6	7	8
   h	8	4	2.7	2	1.6	1.3	1.1	1

   1. On the grid provided, draw a graph to represent the information on the table given. (2 marks)
   2. Use the graph to determine, correct to 1 decimal place, the rate of change of h at = 3. (2 marks)
10. The equation of a trigonometric wave is y = 4 sin (ax - 70)º. The wave has a period of 180º.
    1. Determine the value of a. (1 mark)
    2. Deduce the phase angle of the wave. (1 mark)
11. A point Q is 2000 nm to the West of a point P(40°N, 155°W). Find the longitude of Q to the nearest degree. (3 marks)
12. A box contains 3 brown balls and 9 green balls. The balls are identical except for the colours. Two balls are picked at random without replacement.
    1. Draw a tree diagram to show all the possible outcomes. (1 mark)
    2. Determine the probability that the balls picked are of different colours. (2 marks)
13. The figure below shows triangle XYZ.
    
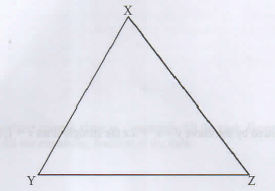
    Using a ruler and a pair of compasses locate point M is 2cm from line YX and is equidistant from lines YX and YZ. Measure length YM (3 marks)
14. The position vectors of points P, Q and Rare OP = 61-23 +3k, OQ = 121 - 5j + 6k and OR = 8i-3j+4k. Show that P, Q and R are collinear points. (3 marks)
15. In a transformation an object of area x cm² is mapped on to an image whose area is 13x cm²
    Given that the matrix of the transformation is   find the possible values of x. (3 marks)
16. Find the area enclosed by the curve y=x²+2x the straight lines x = 1,x= 3 and the x-axis. (3 marks)

SECTION II(50 mks)
Answer only five questions in this section in the spaces provided.

17. Pump P can fill an empty water tank in 7½ hours while pump Q can fill the same tank in 11¼ hours. On a certain day, when the tank was empty, both pumps were opened for 2½ hours.
    1. Determine the fraction of the tank that was still empty at the end of the 2½ hours.(4 marks)
    2. Pump P was later opened alone to completely fill the tank. Determine the time it took pump P to fill the remaining fraction of the tank.(2 marks)
    3. The two pumps P and Q are operated by different proprietors. Water from the full tank was sold for Ksh 15 750. The money was shared between the two proprietors in the ratio of the quantity of water supplied by each.
       Determine the amount of money received by the proprietor of pump P. (4 marks)
18. A rectangular plot measures 50 m by 24 m. A lawn, rectangular in shape, is situated inside the plot with a path surrounding it as shown in the figure below.
    
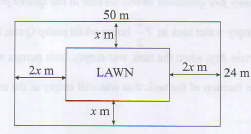
    The width of the path in x m between the lengths of the lawn and those of the plot and 2x m between the widths of the lawn and those of the plot.
    1. Form and simplify an expression in x for the area of the:
       1. lawn; (2 marks)
       2. path.(1 mark)
    2. The area of the path is 1½ times the area of the lawn.
       1. Form an equation in x and hence solve for X (4 marks)
       2. Determine the perimeter of the lawn. (3 marks)
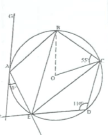
19. In the figure below, points A, B, C, D and E lie on the circumference of a circle centre O. Line FAG is a tangent to the circle at A. Chord DE of the circle is produced to intersect with the tangent at F. Angle FAE = 30°, ZEDC = 110° and 2 OCB = 55°.
    
    
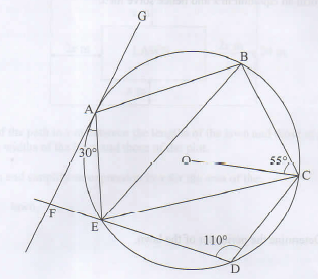
    1. Determine the size of:
       1. ∠ABC
       2. ∠AEB. (3 marks)
    2. Given that AB-5 cm, ED -4.4 cm and FE = 2.5 cm. Calculate correct to 1 decimal place:
       1. the radius of the circle. (2 marks)
       2. the length of line AF. (2 marks)
20. The table below shows income tax rates in a certain year.
    

    Monthly taxable income in Kenya shillings	Tax rates
    0 - 12 298	10%
    12 299 -23 885	15%
    23 886-35 472	20%
    35 473 - 47 059	25%
    47 060 and above	30%

    In the year, the monthly earnings of Kanini were as follows:
    Basic salary : Ksh 64 500 
    House allowance : Ksh 12 000
    Kanini contributes 7.5 % of her basic salary to a pension scheme. This contribution is exempted from taxation. She is entitled to a personal tax relief of Ksh 1 408 per month.
    Calculate:
    1. Kanini's monthly taxable income.(2 m arks)
    2. the tax payable by Kanini that month. (6 marks)
    3. Kanini's net pay that month. (2 marks)
21. The vertices of the triangle shown on the grid are A' (3,-3), B' (1,-1) and C' (3,-1).
    Triangle A'B'C' is the image of triangle ABC under a transformation whose matrix is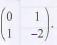 
    
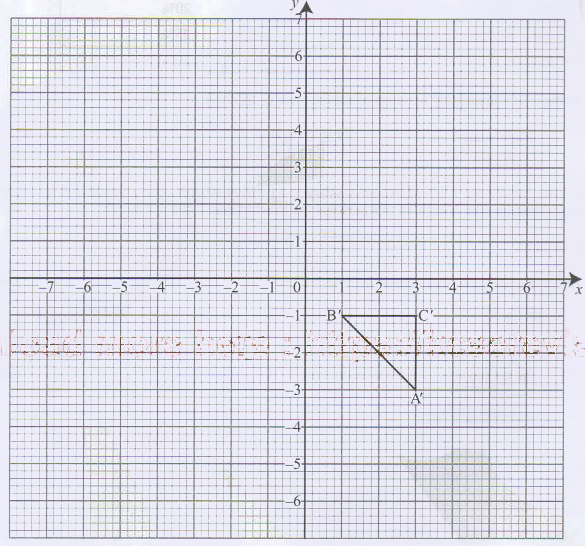
    1. Find the coordinates of triangle A, B and C.(4 marks)
    2. Triangle A"B"C" is the image of triangle A'B'C' under a transformation matrix (2 marks)
       
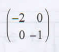
       Determine the coordinates of A", B" and C".
    3. On the same grid provided, draw triangles ABC and A"B"C". (2 marks)
    4. Determine a single matrix that maps ABC onto A"B"C". (2 marks)
22. Workers in a factory commute from their homes to the factory. The table below shows the distances in kilometres, covered by the workers.
    

    Distance (km)	1-5	6-10	11-15	16-20	1-25	26-30
    Number of workers	3	6	t	7	4	2

    The mean distance covered was 14.5 km.
    1. Determine the value of and hence the standard deviation of the distances correct to 2 decimal places. (6 marks)
    2. Calculate, correct to 2 decimal places, the interquartile range of the distances. (4 marks)
23.      
    1. Complete the table below giving the values correct to 1 decimal place.
       

       xº	0	30	60	90	120	150	180	210	240	270	300	330	360
       y=2sin(¾x)-2cos(¾x)	-2	-1.1	0		2		2.8		2	1.1	0		-2
       y= 1 + 2cos x	3		2	1	0	-0.7	-1		0	1		2.7	3

       (2 marks)
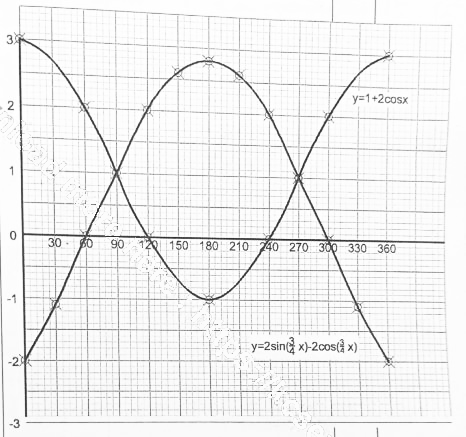
    2. On the grid provided and using the same axis, draw the graphs of y= 2sin(¾x) -2cos(¾x) and y=1+2cos x for 0º ≤ x ≤ 360°. (4 marks)
    3. Using the graphs in part (b):
       1. find the values of x for which sin(¾x)= 1 + cos(¾x) (2 marks)
       2. determine the range of x for which 2sin(¾x)-2cos(¾x)>1 + 2 cos x (2 marks)
24. A particle was moving along a straight line. The acceleration of the particle after t seconds was given by (4t-13) ms^-2. The initial velocity of the particle was 18 ms^-1
    1. Determine the value oft when the particle is momentarily at rest. (5 marks)
    2. Find the distance covered by the particle between the time t = 1 second and t=3 seconds. (5 marks)

MARKING SCHEME

1. Vol. of water geting to the tank in 1sec
   = ²²/₇ x 0.014² x 2
   = 0.001232 m³
   Time needed to fill tank
   =   18.48   
     0.001232
   = 15000 sec
   = 4¹/₆ hours
2. n^th term 2 x 2^n-1
   (n-1)^th term = 2 x 2^n-2
   2 x 2^n-1 x 2 x 2^n-2 = 512
   2^n-1 = 2⁹
   2n - 1 = 9
   n = 5
3. 4 x a x 9 = (-30)²
   a = 900 
          36
   = 25
4. y² =  b ²x  ² 
         cx² - a
   cx² - y² - ay² = b²x²
   cx² - y² - b²x² = ay² 
   x² (cy² - b²) = ay² 
   x = ± √    ay  ² 
              cy² - b²
5. 
   
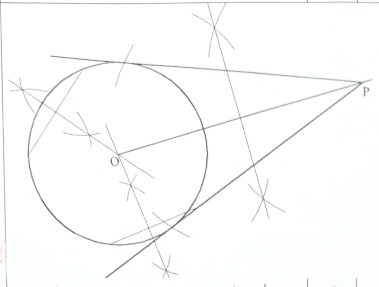
   Locating centre O 
   ⊥ bisector of OP
   Arc showing the correct position of point of contact of circle and tangent
   tangent drawn b utt
6. P = k    √Q    
            (R - S)²
   New value of Pafter changes in Q, R and S
   = k    √1.44Q      
       (0.9R - 0.9S)²
   =1.481k    √Q    
                (R - S)²
   = (1.481 - 1)100
   Thus, P increases by 48.1% or 48.2%
   The word increase is not necessary
7. Let point A' be the projection of point A on the plane GFEH
   AA'= √(5² - 3²)
   = 4
   FA' = √(6² + 8²)
   = 10
   Tanθ = ⁴/₁₀ = 0.4
   θ =21.8º
8. Balance upon paying deposit:
   = 20000 - 10000
   = 10000
   Amount Repaid
   = 900 x 18
   = 16200
   Let r =rate of interest per annum
   
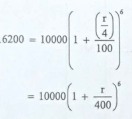
   1 + ^r/₄₀₀ =⁶√1.62 = 1.084
   r = (1.084 - 1)x 400
   = 33.6% or 33.5%
9.         
   1.      
       
   2. Gradient = 0 - 27
                         6 - 3
      = -0.9 ± 0.1
10.       
    1. 360 - 180
         a
       a = 2
    2. Phase Angle = 70º
11. Let θ  = longitude difference between P and Q
    θ x 60 cos 40 = 2000
    θ =    2000    
         60 cos 40 
    = 43.51º
    = 155 + 43.51 = 198.51°
    Longitude of Q
    = 360° - 198.51°
    161°E
    180 - 18.51 
    = 161°E
12.      
    1.    
        
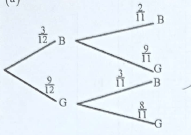
    2. P(Balls picked are of different colours)
       = ³/₁₂ x ⁹/₁₁ + ⁹/₁₂ x ³/₁₁
       = ²⁷/₁₃₂ + ²⁷/₁₃₂
       = ⁵⁴/₁₃₂ 
       Accept ⁹/₂₂
13. 
    
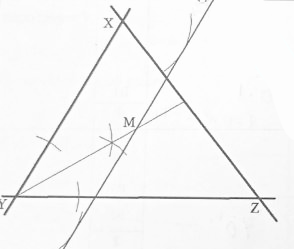
    YM = (4 ± 0.1) cm
    Angle bisector of ∠ XYZ
    construction of a straight line 2 cm from and parallel to line XY
    OW-1 if point M is not marked
14. 
    
    P is a common point
    Points P, Q and R are collinear
15. 3x² - 7(x - 1) - ^13x/_x = 13
    3x² - 7x - 6 = 0
    (3x + 2)(x - 3) = 0 
    x = -²/₃ or x = 3
16. 
    
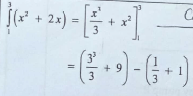
    18 - 1¹/₃
    = 16 ²/₃ sq. units
17.        
    1. Fraction of tank filled by pumps Pand Q in Ihr
       =  1   +  1   =  2  +  4 
          7½  11¼    15    45
       Fraction of tank filled by pumps PandQ in 2½hrs
       = ²/₉ x ⁵/₂
       = ⁵/₉
       Fraction of tank still empty
       = 1 - ⁵/₉
       = ⁴/₉
    2. Time taken by pump P alone to fill ⁴/₉ of the tank
       = ⁴/₉ ÷ ²/₁₅
       = ⁴/₉ x ¹⁵/₂
       = 3¹/₃hrs
    3. Total time Pump P has pumped
       = 2½ + 3¹/₃
       = 5⁵/₆ hrs
       Fraction of tank delivered by pump P
       = ²/₁₅ x 5⁵/₆ 
       = ⁷/₉
       Amount received by propriator of Pump P
       = ⁷/₉  x 15750
       = Ksh 12 250
18.      
    1.      
       1. Area of lawn
          = (50 - 4x)(24 - 2x)
          = 1200 - 100x - 96x + 8x²
          = 1200 - 196x + 8x²
       2. Area of path
          = 50 x 24 - (1200 - 196x + 8x²)
          = 1200 - 1200 + 1960 - 8x²
          = 196x – 8x² 
    2.      
       1. 196x - 8x² = ³/₂(1200 - 196x + 8x²)
          = 1800 - 294x + 12x²
          = 20x² - 490x + 1800
          = 2x² - 49x + 180 = 0
          = (2x - 9)(x - 20) = 0
          = x = 4.5 or x = 20
       2. Length of lawn
          = 50 - 4 x 4.5
          = 32m
          Width of lawn
          = 24 - 2 x 4.5
          = 15m
          Perimeter of lawn
          = 2(32 + 15)
          = 94 m
19.      
    1.      
       1. Size of ∠AEC
          ∠ABE - 30°
          (Angle in alternate segment)
          ∠CBE = 70º
          (Opposite angle of a cyclic quadrilateral)
          ∠AEC - [180 - (30+70)] = 80°
          (Opposite angle of a cyclic quadrilateral)
       2. ∠BOC = 180-2x55 - 70°
          ∠BEC = 35°
          Angle at the circumference is half angle at centre)
          ∠AEB - 80 - 35° = 45°
          
    2.        
       1. Let radius of circle = R
          2R =   5   
                sin 45°
          R = 3.5 cm
       2. AF = √2.5 x (2.5 + 4.4)
          AF = √17.25
          = 4.2 cm
          
20.        
    1. Taxable income
       = 64 500 + 12.000 - ^7.5/₁₀₀ x 64500
       = Ksh 71662.50
    2. Tax payable by Kanini
       1st slab = 12798 x ¹⁰/₁₀₀ = 1229.80
       2nd slab = 11587 x ¹⁵/₁₀₀ =1738.05
       3rd slab = 11587 x ²⁰/₁₀₀ = 2317.4
       4th slab = 11587 x ²⁵/₁₀₀ = 2896.75
       5th slab = 24603 x ³⁰/₁₀₀ = 7381.05
       Total tax = 15563.05
       Tax less relief
       = Ksh 15563.05 - 1408
       = Ksh 14 155.05
    3. Total deductions
       = 14155.05 + ⁷⁵/₁₀₀ x 64 500
       = 18992.55
       Net income =( 64500 + 12000) - 18 992.55
       = 57 507.45
21.      
    1. Inverse of transformation matrix
       
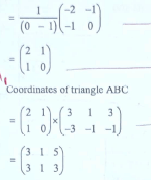
       Coordinates of triangle ABC are A(3, 3), B(1,1) and C(5,3)
    2. Coordinates of triangle A"B"C
       
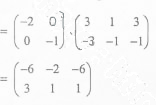
       Coordinates of triangle A'B'C' are A"(-6, 3), B"(-2,1) and C (-6, 1)
    3. ΔABC drawn
       
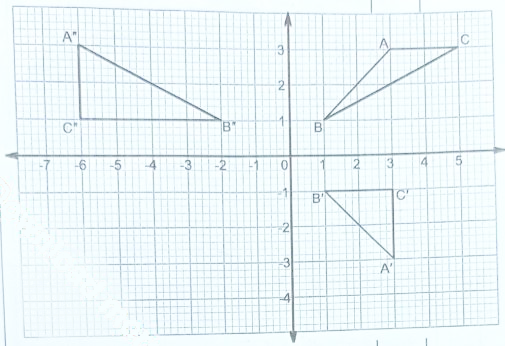
       ΔA'B'C' drawn
    4. Single matrix to map ABC onto A'B'C'
       
22.      
    1. 
       

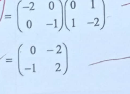
       Midpoint x	f	xf	x2f
       3	3	9	27
       8	6	48	384
       13	t	13t	1352
       18	7	126	2268
       23	4	92	2116
       28	2	56	1568
       	Σf = 22 + t	Σxf = 331 + 13t	Σx2f = 7715

       331 + 13t = 14.5
          22 + t
       Variance = √7715 - 14.5² 
                             30
       = 46.92
       Standard deviation = √46.92
       = 6.85
    2. 
       

       UCB	5.5	10.5	15.5	20.5	25.5	30.5
       C.F	3	9	17	24	28	30

       Q₃  = 15.5 + 5.5 x 5
                             7
       = 19.43
       Q₁ = 5.5 + 4.5 x 5
                          6
       = 9.25
       Interquartile range
       Q3 - Q1 = 19.43 - 9.25
       =10.18
23.          
    1. 
       

       x	30º	90º	150º	210º	300º	330º
       2sin(¾x) - 2cos2sin(¾x)		1.1	2.6	2.6		1.1
       1 + 2cos x	2.7			-0.7	2

       Allow 7
       B1 for any 5
       
    2.      
       1. When y=2
          2sin(¾x) - 2cos(¾x)= 2 then
          sin(¾x) = 1 + sin(¾x)
          x = 120º and x = 240º
       2. 87º < x < 273
          ± 2º
24.      
    1. v = ∫(4t - 13)dt
       = 2t² -13t+ c
       when t = 0, v = 18
       18 - 2 x 0 - 13 x 0 + c
       c = 18
       v = 2t² - 13t + 18
       When v-0
       2t² -13t + 18 = 0 
       = (2t - 9)(t - 2) = 0
       t = 4.5 or t = 2
    2. Distance covered by particle
       Area above x axis
       ²₁∫(2t² - 13t + 18)dt
       = [²/₃t³ - ¹³/₂t² + 18t]²₁
       =[²/₃ x 2³ - ¹³/₂ x 2² + 18 x 2] - [²/₃ x 1³ - 13/2 x 1² + 18 x 1]
       =[¹⁶/₃ - 26 + 36]-[²/₃ - ¹³/₂ + 18]
       = 15¹/₃ - 12¹/₆
       3¹/₆
       Area below x axis
       =[²/₃ x 3³ - ¹³/₂ x 3² + 18 x 3] - 15¹/₃
       =[18 - ¹¹⁷/₂ + 54] - 15¹/₃
       = 1⁵/₆
       Total area
       = 3¹/₆ + 1⁵/₆ 
       = 5m