Instructions To Candidates
- This paper contains two sections: section I and section II
- Show all the steps in your calculations, giving your answers at each stage.
- Marks may be given for correct working even if the answer is wrong.
- Non programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.

Questions
SECTION A (50 MARKS)
Answer all questions in the spaces provided
- If log x =1.813 and log y = 2.513, find the value of xy2 (3 mks)
- There are 360 pupils in Bidii primary school. There are twice as many girls as there are boys. On one day; 1/5 of the boys were absent and the same number of girls were absent on that day. What is the ratio of boys to girls, who were present on that day?(3mks)
- The diagram below shows a rectangular plate 2acm wide and 3acm long with a square piece of side bcm cut out. Calculate
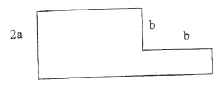
- The perimeter(2mks)
- The area of the plate(2mks)
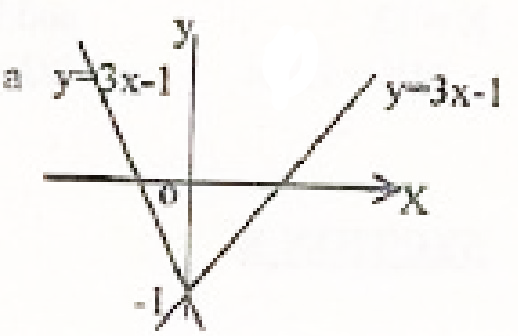
- If the line y=3x -1 is reflected in the y axis, find the equation of the image.(3mks)
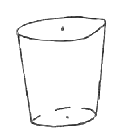
- The figure below shows a rectangle ABCD where AB=2m and AD=1m which forms the open top of a water container of semi-circular cross-section. Calculate the capacity of the container if the depth of the water at the deepest point is 0.2m. Use pie as 22/7.(4mks)
- A particle is moving with an initial speed of 4m/s. In the next four seconds its speed increases uniformly to 10m/s and then the speed decreases uniformly until the particle stops, moving after a further eight seconds. Find
- The total distance travelled by the particle(3mks)
- The acceleration in the last eight seconds(1mk)
- Find the total surface area of a solid hemisphere of radius 7cm(3mks)
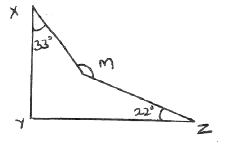
- Find the value of the reflex angle of m in the diagram below.(2mks)
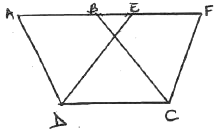
- In the figure below, ABCD and CDEF are parallelograms. Line ABEF is a straight line If AF=11cm and BE=3cm. Find the length of DC (3mks)
- Find two consecutive odd numbers such that 6 times the smaller added to 4 times the greater comes to 138. (3mks)
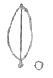
- The figure below shows part of a certain school badge. Taking O as a centre, complete the diagram under order 6.(3mks)
- A chord 6.6cm long is 5.6cm from the centre of a circle. Calculate the length of ab chord which is 6.3cm from the centre of the circle. (3mks)
- The angles of elevation of the highest point of a building from two points S and T are 60° and 30°. T is vertically above S and ST=10M. Calculate the height of the building above the level of S. (4mks)
- The mean of 10 observations is 12.5 while calculating the mean one of the reading was mistaken as (-9) instead of (+9). Find the correct mean (2mks)
- Use reciprocal and square root tables to evaluate(3mks)
3 - 1
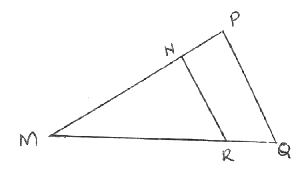
0.3752 √7231 - In the figure below NR is parallel to PQ. MN=7.5cm, NP=2.5cm, MR=9cm and PQ =8cm. Find NR and RQ (3mks)
SECTION B (50 MARKS)
Answer all questions in the spaces provided
- Using a suitable scale, draw x and y axis for -4 ≤ X ≤10 and -4 ≤ y ≤ 12.
- Draw a triangle with vertices (-1,1), (-1,10), (-4,7) and label it F. (3mks)
- A transformation R maps triangle F onto the triangle R(F) which has vertices (0,-2), (9,-2) and (6, 1). Draw the triangle R(F) and describe R fully.(3mks)
- M is a reflection in the line y=x. Find, by drawing, the coordinate of the vertices of the triangle M(F) (4mks)
-
- Find the equations of the sides of a triangle which has vertices A(0,0), B(7,0) and C(5,6) (6mks)
- Lines r and s both pass through the point (k, 9). Liner has a gradient of 4/3 and passes through the point (5, -3).
- Find the value of k (2mks)
- Find the equation of line s given that it crosses the x-axis at (-14,0)(2mks)
- Every year a school takes 42 students accompanied by 7 adults to ASK show. In 2013, the reduced fare for a student was. sh.24.50 and this was two third of the adul fare. For every complete group of 10 students in the party, one of the adults was allowed to travel without paying.
- What was the total cost of the journey(4mks)
- The full fare for a student going to the show was sh.29.40. Find the percentage reduction granted to a student who travelled with school party. (2mks)
- In 2014, a student's full fare was increased to sh.36.00. The fare for school party was increased in the same proportion. Find the fare for a student travelling with the school party in 2014.(4mks)
- The distance between two towns A and B is 360km. A minibus left A at 8.15am and travelled towards B at an average speed of 90km/h. A matatu left B at 10.35am on the same day and travelled towards A at an average speed of 110km/h?
- How far from A did they meet? (4mks)
- At what time did the two vehicle meet (2mks)
- A motorist started from his home at 10.30 am on the same day and travelled at 100km/h. He arrived at B at the same time as the minibus. Calculate the distance from B to his home.(4mks)
- The figure below shows a solid frustum of a cone. The radii of the circular ends are 2.8cm and 1.4cm. The slanting height of the frustum is 12cm.
Calculate- The volume of the frustum(4mks)
- The surface area of the frustum(4mks)
- The frustum was melted to form a solid cube. In the process 15% of the metal was lost. Calculate the length of the cube formed. (2mks)








Marking Scheme
SECTION A
- Log xy2 - Log x + 2log y
1.813 + 2 (2.513)
1.813 +3,026 = 2.83g
PX2-102.83g-0.069 - girls boys
240 120
1/5 x 120=24 ∴ 96
216 ∴ 96
Ratio 9:4
Ratio of boys to girls 4:9 -
- 3b + 2a +(36 -b) + (2a - b)
3b +2b + 2a + 2a-b-(4a + 4b)cm - (28 . 3b)-(6.b)
(6ab-b2)
- 3b + 2a +(36 -b) + (2a - b)
-
-
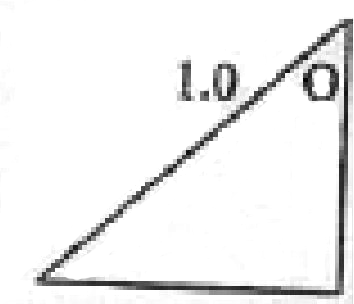
θ=36.86
2θ = 73.74
BA - 73.74 x ²²/₇ x12
360
= 0.6438m2
Area of triangle = 1/2 x 1 x 1 sin7
= 0.48
∴ BA=0.6438 -0.48
=0.16.38m2
Vol. = BA XH -0.1638m2
Capacity - 163.8litres -
-
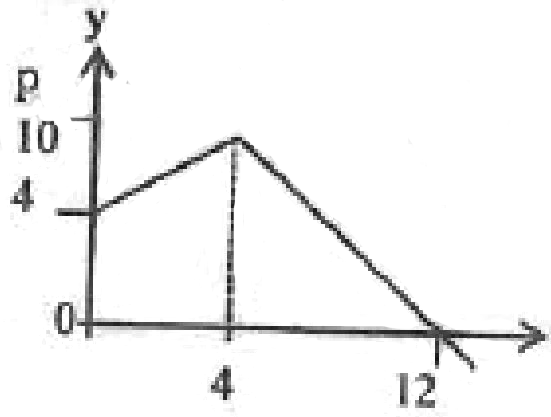
Time (sec)
Area under graph
(4+ 10) x 4+ ½ x 8 x 10
2
(7 x 4) +(40) = 68m - Fv-1V = 0-10 = ⁵/₄ = -1¼ m/s or -1.25m/s
TT 8
-
- πr2 +4/2 πr2
(22/7 x 72) + (2 x 22/7 x 72)
154 + 308
= 462cm2 - 33 +22-55º
m= 145º
Reflex = 215° - 11-3 - 8 ÷ 2 = 4
DC = 4cm
Opposite sides of a ↑↑
Gran and equal - Let the nos.be X, X + 2
6(x) + 4(x+2) = 138
6x + 4x+8 = 138
10x=130
X = 13
13, 15 - 360 = 60°
6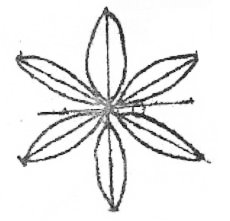
- H = 6.5
5.62 +3.32= H2
H=6.5
6.5-6.32 = X2
X=1.6
2x = 3.2cm - Tan 30 - x/d
1 = x
√3 d
D=x√3
Tan60° = x +10
d
d= x+ 10
√3
x√3 = x +10
√3
3x = x +10
2x = 10
x=5
AB = 10 + 5 = 15m - x = Σfx = 12.5 x 10 = Σfx
Σf
Σf = 10
125 + 9+9=143
Σf =10
x=143
10
=14.3 - 3 - 1
0.3752 √72.31
3 1 - 1
0.3752 8.5035
√72.31 = 8.5035
3 x 1 + 1
0.3752x10-1 8.5035
3 (0.2666 x 101) + (0.1175)
3(2.666) + 0.1175
= 7.998 +0.1175 = 8.1155
= 8.116 - MP = MQ = PQ also 8 = 10
MN MR NR y 7.5
10 = x 60 = 10y
7.5 9 y 6
90 = 7.5 NR = 6cm
X = 12 and RQ = 12-9
MX = 12cm RQ = 3cm
SECTION B
-
- A translation of vector (10)followed by a rotation centre (0,1) about -90° and finally a translation of vector (0-3)
OR Accept matrix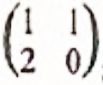 and description
and description
See calculation - (1,-1)
(10,-1)
(7, -4)
-
- AB= 0-0 = 0 =0
7-0 7
AB = y=0
AC = 6-0 = 6
5-0 5
Y-0 = 6
x-0 5
5y = 6x
AC = y = 6/5x
BC = 6-0 = 6 = -3
5-7 -2
y-0 = -3
X-7 1
BC y=-3x+21 -
- r= y +3 = 4
X-5 3
X = 14
(k, 8) (14,9)
k= 14
3y + g = 4x - 20
3y = 4x -2g
when y- g
3(g) = 4x - 2g
27 = 4x-2g
4x=56 - (14,9) (-14, 0)
28y- 9x = 126
9 - 0 = 9
14 - - 14 28
Y - 0 = 9
x +14 28
28y = 9x + 126
- r= y +3 = 4
- AB= 0-0 = 0 =0
-
- Students = 42, Adults 7
@ sh24.50 @sh 36.75
Students Adults
(24.3% 42) + (36.75 x 3)
1029 +110.25
sh. 1, 139,25 - 100% = 29.40
1% = 29.40
29.40 - 100%
1 = 100
29.40
24.50 = 100 x 24.50
29.40
= 83 1/3 %
Reduction was 16 2/3% - 36.00 x 24.50
29.40
sh 30
- Students = 42, Adults 7
-
- A | 360km |B
8:15am 10:35am
90km/h 110km/h
B4, B started, R. Speed - 110 +90
=90 x 2 1/3 =200kh
=210km Time used= D/S= 150/200
Dist left = 150 45min
10:35
8:15
2:20
Dist = sxt
¾ x 90
=6.5th
From A
277.5km - 10.35am
+ 45 min
11.20am
Met at 11.20am - Time taken by A to B
T =D/S = 360/90 = 4hrs
Arrived at
8.15
4.00
12.15
Time by motorist =
12.15
-10.30
1.45
Dist= sxt
100 x 1.75 = 175km
- A | 360km |B
-
- Vol. 1/3ΠR2H - 1/3Πr2h
1/3Π[(2.82 x 23.84) -(1.42 x 11.92)]
1/3Π(163.5816) =
=171.37cm3 - ΠR2 + Πr2 + (ΠDH - Πdh)
22/7 x 2.82 + 22/7 x 1.42 +
[(22/7 x 2 x 2.8 x 23.84) - (22/7 x 2 x 1.4 x 11.92)]
24.64 + 6.16 + (209.792-104.896)
24.64 + 6.16 + 104.896 =135.696cm2 - 85 x 171.37 - 145.6645cm3 = 3√145.6645 = 5.2616cm
100
- Vol. 1/3ΠR2H - 1/3Πr2h
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - KCSE Prediction Papers 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students