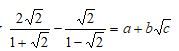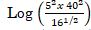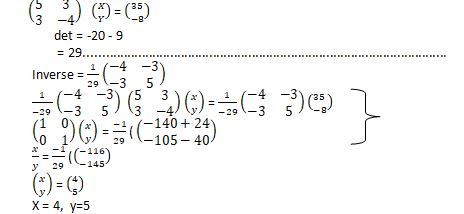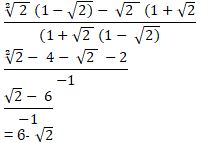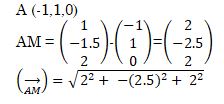MATHEMATICS
PAPER 2
TIME: 2 ½ HOURS
INSTRUCTIONS
- This paper consist of TWO sections: section I and Section II.
- Answer ALL the questions in Section I and only five questions from section II.
- Show all the steps in your calculations, giving your answers at each stage in the stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
SECTION I : 50 MARKS.
ANSWER ALL THE QUESTIONS
- Evaluate without using Mathematical tables or a calculator. (3mks)
2log 5 - 1/2log 16 + log40 - The sum of K terms of sequence 3,9,15,21............is 7500. Determine the value of K. (3mks)
- Use matrix method to solve (3mks)
5x +3y =35
3x -4y = -8 - Calculate the percentage error in the volume of a cone whose radius is 9.0cm and slant length 15.0cm. (3mks)
- Make y the subject the subject of the formula (3mks)
p/w = (my-2)/(ny+4) - Solve for x: tan2 x – 2 tan x = 3 for the interval 0 ≤x≤ 180o (3 marks)
- The table below shows income tax rates in the year 2013.
In that year, a monthly personal tax relief of ksh 1056 was allowed. Calculate the monthly income tax by a constable who earned a monthly salary of ksh. 42500 (3mks)Monthly Income in Ksh Tax rate in each shilling Up to 9680 10% 9681-18800 15% 18801 – 27920 20% 27921 – 37040 25% Over 37040 30% - Simplify leaving your answer in the form a+b√c, where a, b and c are rational numbers. (3mks)
-
- Expand (1-n)5 (2mks)
- Use the expansion in (a) up to the term in n3 to approximate the value of (0.98)5 (2mks)
- The probability that three candidates; Anthony, Beatrice and Caleb will pass an examination are 3/4, 2/3 and 4/5 and respectfully. Find the probability that:-all the three candidates will not pass. (2mks)
- The equation of a circle is X2 + Y2 -4x +6y + 4 = 0. On the graph provided draw the circle (4mks)
- Find the shortest distance between points A(50oS,25ot) and B(50oS, 140oE in KM (Take R=6370 Km) (3mks)
→ - The mid-point of AB is (1,-1.5, 2) and the position vector of a point A is -1+j is . Find the magnitude of AB correct to 1dp. (3mks
- Without using a calculator or mathematical tables. Express in surd form and simplify (3mks)
3
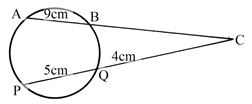
1-COS 300 - The figure below shows a circle centre O. AB and PQ are chords intersecting externally at a point C. AB = 9cm, PQ= 5cm and QC = 4cm. Find the length of BC. (3mks)
- Evaluate without using tables
Log(3x+8) -3log2 = log(x-4) (4mks)
SECTION II (50 MARKS)
Answer ONLY FIVE questions in this section
-
- Use the trapezium rule with six trapezia to excrete the areas bounded by the curve Y=2n2+ 3n +1, the axis and the ordinate x=0 and x=3. (5mks)
- Calculate the exact axed in (a) above by integration. (3mks)
- Assuming they are calculated in (a) above is an estimate, calculate the percentage error made when the trapezium rule is used leaving your answer to 2 decimal places. (2mks
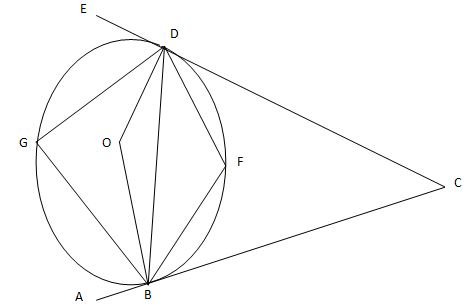
- In the diagram below <EDG=360 and <ABG=420 Line EDC and ABC are tangents to the circle at D and B respectively.
Calculate by giving reason- <DGB (2mks)
- Obtuse <DOB (2mks)
- <GDB (2mks)
- <DCB (2mks)
- <DFB (2mks
- The table below shows the rate at which income tax is charged for all income earned in a month in 2015.
Taxable Income p.m (Kenya pound) Rate in % per Kenya pound
1 -236 10%
237 -472 15%
473 -708 20%
709 – 944 25%
945 and over 30%
Mrs.mumanyi earns a basic salary of 18000.She is entitled to a house allowance of Ksh. 6,000 a person relief of Ksh. 1064 month
Every month she pays the following.- Electricity bill shs.580
- Water bill shs. 360
- Co-operative shares shs. 800
- Loan repayment Ksh. 3000
- Calculate her taxable income in k£ p.m (2Marks)
- Calculate her P.A.Y.E (6Marks)
- Calculate her net salary (2Marks)
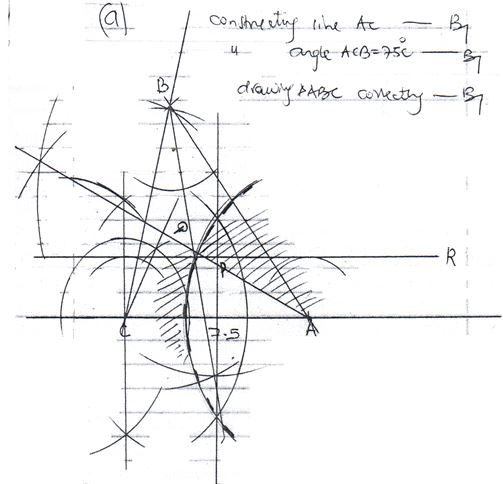
- A flower garden is in the shape of a triangle ABC such that AB = 9M, AC=7.5M and angle ACB=75%. Using a rule and a pair of compass only.
- Construct ΔABC (3mks)
- Construct a locus of P such that AP = pc (2mks
- Construct locus of Q such that it is equal distance from AB and BC and locus of R which is 2M from AC. (2mks)
- Flowers are to be planted such that they are nearer AC than AB and less than 5m from a shade the portion with flowers. (3mks)
- A tank has two water taps P and Q and another tap R. When empty the tank be filled by tap P alone in 5 hours or by tap Q in 3 hours .When full the tank can be emptied in 8 hours by tap R
- The tank is initially empty . Find how long it would take to fill up the tank
- If tap R is closed and taps P and Q are opened at the same time (2mks)
- If all the three taps are opened at the same time .Giving your answer to the nearest minute (2mks)
- Assume the tank initially empty and the three taps are opened as follows
P at 8:00 am
Q at 9:00 am
R at 9:00 am- Find the fraction of the time that would be filled by 10:00 am (3mks)
- Find the time the tank would be fully filled up. Give your answer to the nearest minute (3mks)
- The tank is initially empty . Find how long it would take to fill up the tank
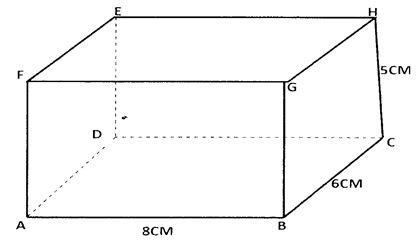
- The figure below shows a cuboid.
Calculate- The length BE (2Mks)
- The angle between BE and plane ABCD (3Mks)
- The angle between FH and BC. (2Mks)
- The angle between place AGHD and plane ABCD. (3Mks)
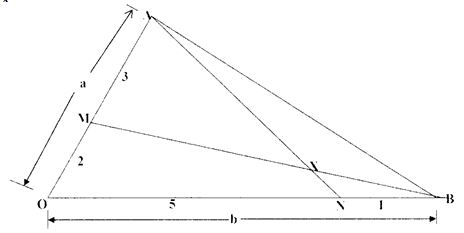
- In triangle OAB below OA = a, OB = b point M lies on ON such that OM : MA= 2:3 and point N lies on OB such that ON: NB = 5:1 line AN intersect line MB at X.
- Express in terms of a and b
- AN (1mk
- BM (1mk)
- Given that AX=kAN and BX=rBM where k and r are scalars.
- write down two different expression for OX in terms of a, b, k and r. (2mks)
- Find the value of k and r. (4mks)
- Determine the ratio in which x divides line MB. (2mks)
- Express in terms of a and b
-
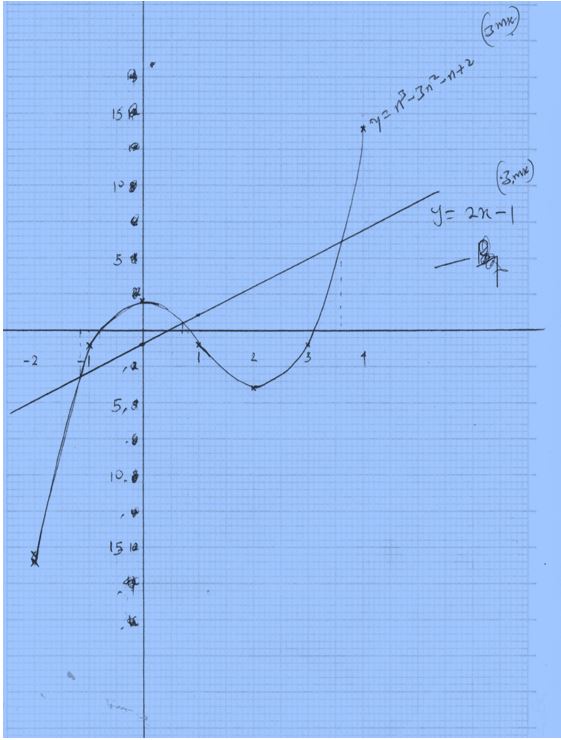
- Complete the table below for the function y=n3-3k2-k+2 for -2 ≤n ≤4. (2mks)
X -2 -1 0 1 3 4 Y -6 2 14 - On the grid provided, draw the graph of y =n3-3n2-n+2. (3mks)
- Use the graph to solve the equation
n3 -3n2 – x + 2 = 0 (2mk) - By drawing a suitable line on the graph, solve the equation n3- 3n3 – 3n + 3 = 0 (3mks)
- Complete the table below for the function y=n3-3k2-k+2 for -2 ≤n ≤4. (2mks)
MARKING SCHEME
-
Log (25x1600/4)
Log 10,000
4 log 10
=4 - n=? δn=n/2 (2a+(n-1)d)
a=3
d=6
δn=7500
7500=n/2 [2(3)+(n-1)6]
7500=n/2 [6+6n-6]
7500=n/2(6n)
7500=3n2
n2=2500
n=50 -
- 8.95 – 9.05
14.5 – 15.5
Max=1/3 x 22/7 x 9.052 x 15.5=132.94
Min = 1/3 x 22/7 x 8.92 x 14.5=1216.80
Actual = 1/3 x 22/7 x 92 x 15=1272.86
A.E = 1/2(1329.94-1216.80
=56.57
%error = 56.57/1272.86 x 100
=4.445% - P/w = (my-2)/(ny+4)
Pny + 4p = mwy – 2w
4p+2w = mwy – pny
4p +2w = (mw – pn) y
y= (4p+2w)/(mw-pn) - tan2x – 2 tan x -3=0
Let tan x be P
P2-2p -3=0
P(p-3) + 1(p-3)=0
(p-3)(p+1)=0
P=3 or p=-1
tan x =3
x=71.57o or x = 135o - 1st tax band = 9680 x 10/100 = 968
2nd tax band = 9120 x 15/100 = 1368
3rd tax band = 9120 x 20/100 = 1824
4th tax band = 9120 x 25/100 = 2280
5th tax band = 5460 x 30/100 = 1638
Gross tax = 8078..............................................
Relief = 1056
Net tax = 7022
Monthly income tax = 7022 -
-
(1-n)5=1-5n+10n2-10n2+5n4-n5X5 15 14 13 12 11 10 Y 0 (-n)1 (-n)2 (-n)3 (-n)1 (-n)5 coeff 1 5 10 10 5 1 1 -5n -10n2 -10n3 5n4 -n5 - (0.98)5 = (1-0.02)5 = (1-n)5
= 0.02=n
1-5(0.02) + 10(0.02)2 -10(0.02)3
1-0.01+0.004-0.00008 = 0.99392
- P(fail) = 1/2 x 1/3 x 1/5 = 1/60
- x2+y2-4x+6y+4=0
x2-4x+y2+6y=-4
(x2-4x + (-2)2+(y2+6y+(3)2=-4+(-2)2+(3)2
(x-y)2+(y+3)2=9
Centre =(2,-3)
Radius =3 - A(50oS, 25oE)
B(50oS, 140oE) θ= 140-25
long
θ, ∝ θ=115o
km =θ/360 2π2
115 o x 2 x 22/7 x 6370
360
= 12,790.56km -
= √(4+6.25+4)
= √14.25
= 3.775 x 2
= 7.550
=7.6 - Cos 30º = √3/2
3/1-cos 30º = 3
1- 3/2
=6/2-√3
=6/2-√3 x (2+√3)/(2+√3) = 12+6√3/4+2√3 - 2√3 -3 - y(y+9) = 4x9
y2+9y-36=0
y2 + 12y-3y-36=0
y(y+12)-3(y+12)=0
(y-3) (y-12) = 0...................................................
Y=3 or y=-12(ignore)
∴ = BC = 3cm - Log (3x+8) – lof 8 = 10g (x – 4)
Log (3x+8/8) = log (x-4)drop logs
3x+8/8 x – 4
3x+8=8x-32
3x – 8x = -32 -8
-5x = -40
X=8 -
A= ½ h[(yo + yn) + 2(y1 +y2+y3+y4+y5)]X 0 0.5 1 1.5 2 2.5 3 Y 1 3 6 10 15 21 28
= ½ (0.5) [(1+28) + 2(3+6+10+25+21)]
= ¼ x 139
= 34.75- ∫03(2x2 + 3x+)dx
=[2x3 + 3x2 + x (30)
3 2
=2/3 X 27 + 3/2 X 9+ 3
=18/1 + 27/2 + 3/1
=(36+27+6)/2
= 69/2
= 34.5 - Error = actual estimate
34.5 – 34.75
= -0.25
%error = - 0.25/34.5 x 100
= 0.725 decrease
-
- <DGB=78º(Angles alternate segment are equal subtended by the same chord)
- Obtuse <DOB = 156º subtended at the centre by BD is twice the angles subtended at the circumference by BD
- <GDB= 54º (<chord and tangent)
- <DCB=180º(2x78)=24º
angles in a triangle add up to 180º - <DFB=180º-78º=102º
opposition angle in a cyclic
Quadilateral add up to 180º
-
- T.T = (18000+6000)/20
= £ 1200 p.m - 1st 236 x 10/100 = 23.6
2nd 236 x 15/100 = 35.4
3rd 236 x 20/100 = 47.2
4th 236 x 25/100 = 59
- T.T = (18000+6000)/20
-
- Constructing bisector of line AC
locating locus P - Bisecting angle ABC (locus Q)
constructing a line 2cm away from AC locating locus R - Bisecting < BAC
drawing an arc (dotted) 5cm away from A.
Shading unwanted side - Tap P in 1 hour = 1/5 of tank
Tap Q in 1 hour= 1/3 of tank
Tap R empties= 1/8 of tank
-
-
- 1/5+1/3= 8/15
Time = 1 ÷ 8/15
= 1 x 15/8 = 1.875 hour
= 1 hour 53 min - 1/5+1/3-1/8 = 24+40-15 = 49
120 120
Time= 1 ÷ 49/120
=1 x 120/49= 2.44898
=2hrs 27 min
- 1/5+1/3= 8/15
-
- Pin 1 hr = 1/5
in 2hrs = 2 x 1/5 = 2/5
Q in 1hr = 1/3
1/3 x 1= 1/3
R=1/8 x 1
Fractional filled = 2/5 + 1/4 -1/8 = 73/100 - in 1 hr= 49/120
x= 47//120
x= 47/120 x 120/49 = 0.9592=58 min
- Pin 1 hr = 1/5
-
-
- SOH CAH TOA
H2= 82 + 62
=64+36= 100
√100=10 - Tan θ= 5/10
θ = tan-1 0.5=26.56 - Tan θ = 8/6
θ= tan-1 1.333
=53.12 - Tan θ = 5/8= 0.625
θ=tan-1 0.625=32
- SOH CAH TOA
-
-
- AN= AO + ON
= -a + 5/6 B
= -a + 5/6 b - BM=BO+OM
= -b + 2/5OA
= -b + 2/5a
- AN= AO + ON
-
- OX= OB +BX
=b + rBM
=b+ r(b+2/5a)
=b-rb +2/5ra
(1-r)b + 2/5ra
OX=OA+AX
=OA + kAN
= a + k(-a + 5/6b)
=a - ka + 5/6kb
=(1-k)a + 5/6kb - OX = OX
=(1-r)b + 2/5ra=(1-k)a+ 5/6 kb
(1-r)b = 5/6kb
1-r = 5/6k
2/5ra = (1-k)a
2/5r = 1-k
r=5/2(1-k)
=5/2 -5/2k
1-5/6k= 5/2 - 5/2k
-5/6k + 5/2k= 5/2 -1
-5k+15k = 5-2
6 2
10k/6 = 3/2
k= 3/2 x 6/10 = 9/10
r=1-5/6k
1-5/6(9/10)
1-3/4
=1/4 - BX = rBM
BX= 1/4BM
BX/BM = 1/4
MX:XB
3:1
- OX= OB +BX
-
-
-
X -2 -1 0 1 2 3 4 Y -16 -1 2 -1 -4 -1 - Graph drawn
-
- y = n3 - 3n2 - n + 2
o= n3 - 3n2 - n + 2
y=0
x = 0.8 ± 0.05 or 0.9 ± 0.05 0r 3.1 ± 0.05 - y = n3 - 3n2 - n + 2
o= n3 - 3n2 - 3n + 3
y= 2n-1
k = -1.1 ± 0.05 or 0.7 ± 0.05 or 3.6 ± 0.05x 0 1 y -1 1
- y = n3 - 3n2 - n + 2
-
Download Mathematics Paper 2 Questions and Answers - Meru Central Cluster Exam 2020.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students