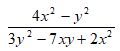MATHEMATICS
PAPER 1
TIME: 2 ½ HOURS
INSTRUCTIONS
- This paper consist of TWO sections: section I and Section II.
- Answer ALL the questions in Section I and only five questions from section II.
- Show all the steps in your calculations, giving your answers at each stage in the stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
SECTION 1: 50 MARKS.
ANSWER ALL THE QUESTIONS
- Evaluate: (3mks)
- A Kenyan businessman bought goods from Japan worthy 2,950,000 Japanese yen. On arrival in Kenya, custom duty of 20% was charged on the value of the goods. If the exchange rate were as follows:-
1 US dollar = 118 Japanese Yen
1US dollar = 76 Kenyan shillings Calculate the duty paid in Kenyan shillings. (3mks) - A rally car travelled for 2 hours 40 minutes at an average speed of 120km/h. the car consumes an average of 1 litre of fuel for every 4 kilometers. A litre of fuel costs Ksh.59. Calculate the amount of money spent on fuel. (3mks)
- The curved surface area of a cylindrical container is 1980cm2. If the radius of the container is 21cm, calculate to one decimal place the capacity of the container in litres (4 mks)
- Given that sinθ= 5/13, find tan(90-θ) in its simplest form. (2mks)
- The equation of line L1 is 2x -5y – 10 = 0. Find the equation of line L2 perpendicular to L1 and passing through (5, -2) express your equation in the form y=mx + c (3mks)
- One interior angle of a polygon is equal to 800 and each of the other interior angles are 128°. Find the number of sides of the polygon. (3 mks)
- The length of a rectangle is (3x + 1) cm, its width is 3 cm shorter than its length. Given that the area of the rectangle is 28cm2, find its length, (3 marks)
- Simplify the expression. (3mks)
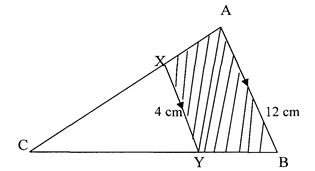
- In the figure below, lines AB and XY are parallel.
If the area of the shaded region is 36 cm2, find the area of triangle CXY. (3 marks) -
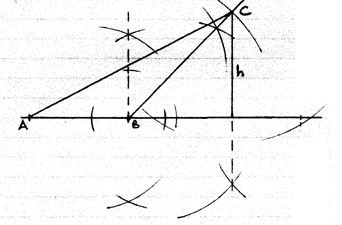
- Using a pair of compasses and a ruler only construct a triangle ABC and such that AB= 4cm, BC =6cm and angle ABC=135o. (2mks)
- Construct the height of triangle ABC in (a) above taking AB as the base, hence Calculate the area of triangle ABC. (2 mks)
- The external length width and height of an open rectangular container are 41cm, 21cm and 15.5cm respectively. The thickness of the materials making the container is 5mm. If the container has 8 litres of water. Calculate the internal height above the water level. (3mks)
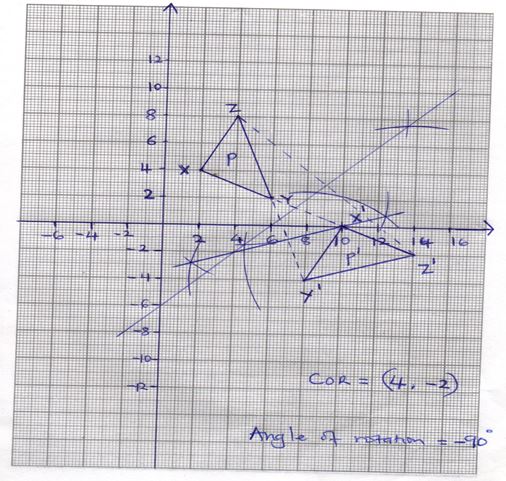
- A triangle P with vertices x(2,4), Y(6,2) and z(4,8) is mapped onto triangle P1 with vertices X1 (10,0), Y1(8, -4) and Z1(14, -2) by a rotation.
- On the grid provided, draw triangle P and its image (2mks)
- Determine the centre and angle of rotation that maps P onto P1 (2mks)
- Solve the following inequalities and state the integral values (3mks)
2x – 2 ≤ 3x + 1 <x + 11 - In the triangle PQR below, PQ =12cm, <PQR = 800 and <PRQ= 300
Calculate, to 4 s.f, the area of the triangle PQR (3mks) - A two digit number is such that the sum of digits in 13. When the digits are interchanged, the original number is increased by 9. Find the original number. (3mks)
SECTION II (50 MARKS)
Answer only five questions in this section
- A straight line L1 has a gradient ˉ½ and passes through point P (-1, 3). Another line L2 passes through the points Q (1, -3) and R (3, 5). Find.
- The equation of L1. (2mks
- The equation of L2 in the from ax+by+c=0 (2mks)
- The equation of a line passing through a point S (0, 1.5) and is perpendicular to L2. (3mks
- The point of intersection of a line passing through S and L2 (3mks)
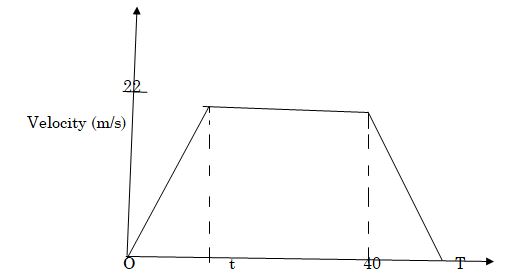
- The figure below shows a velocity – time graph of a car journey.
The car starts from rest and accelerates at 2.75m/s2 for t seconds until its speed is 22m/s. It then travels at this velocity until 40 seconds after starting. Its breaks bring it uniformly to rest. The total journey is 847m long and takes T seconds.
Calculate the- Value of t (3mks)
- Distance travelled during the first t seconds (2mks)
- Value of T (3mks)
- Final deceleration (2mks)
- In the figure below, QT = a and QP = b.
- Express the vector PT in terms of a and b. (1mk)
- If PX = kPT, express QX in terms of a, b and k, where k is a scala. (3mks)
- If QR = 3a and RS = 2b, write down an expression for QS in terms of a and b. (1mk)
- If QX = tQS, use your result in (b) and (c) to find the value of k and t. (4mks)
- Find the ratio PX : XT. (1mk
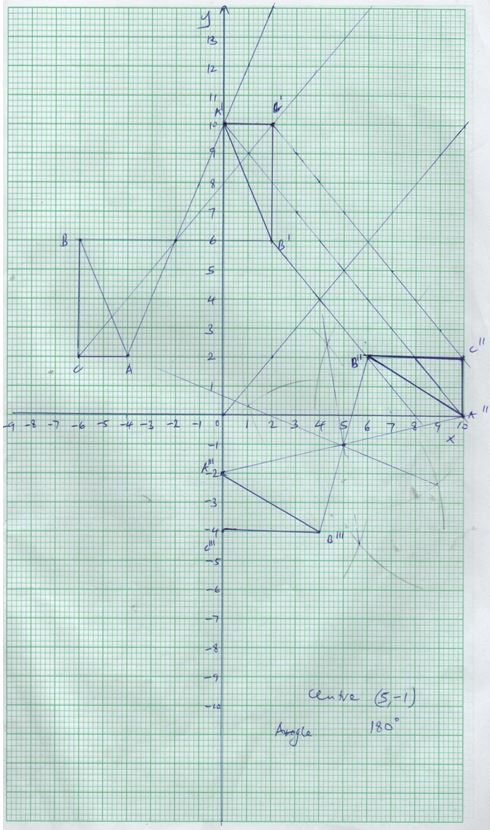
- A triangle with A(-4, 2), B(-6, 6) and C(-6, 2) is enlarged by a scale factor -1 and centre (-2, 6) to produce triangle A¹B¹C¹.
- Draw triangle ABC and A¹B¹C¹.and state its coordinates 4mk
- Triangle A¹B¹C¹ is then reflected in the line y = to give triangle A¹¹B¹¹C¹¹.draw A¹¹B¹¹C¹¹.and state its coordinates 3mk
- If triangle A¹¹B¹¹C¹¹ is mapped onto A¹¹¹B¹¹¹C¹¹¹ whose co-ordinates are A¹¹¹(0, -2), B¹¹¹(4, -4) and C¹¹¹(0, -4) by a rotation. Find the centre and angle of rotation. (3mks)
- Four towns P, R, T and S are such that R is 80km directly to the north of P and T is on a bearing of 290° from P at a distance of 65km. S is on a bearing of 330° from T and a distance of 30 km. Using a scale of 1cm to represent 10km, make an accurate scale drawing to show the relative position of the towns. (4mks)
Find:- The distance and the bearing of R from T (3mks)
- The distance and the bearing of S from R (2mks)
- The bearing of P from S (1mk)
- Four towns A, B, C and D are such that B is 80km directly North of A and C is on a bearing of 3000 from A at a distance of 50km. D is on a bearing of 3450 from C at a distance of 30km.
- Using a scale of 1cm rep 10km, draw the relative positions of the towns (4mks)
- Find:
- The distance and bearing of B from C (2mks)
- The distance and bearing of B from D (2mks)
- Calculate the distance of ABCD (2mks)
- A school in Meru Central decided to buy x calculators for its students for a total cost of ksh. 16,200. The supplier agreed to offer a discount of ksh. 60 per calculator. The school was then able to get three extra calculators for the same amount of money.
- Write an expression in terms of x , for the
- Original price of each calculator (1mk
- Price of each calculator after the discount (1mk)
- Form an equation in x and hence determine the number of calculators the school bought (5mks)
- Calculate the discount offered to the school as a percentage (3mks)
- Write an expression in terms of x , for the
- 20.A solid is made up of a conical frustum and a hemispherical top. The slant height of the frustum is 8cm and its base radius is 3.5cm. If the radius of the hemispherical top is 4.2cm.
- Find the area of
- The circular base. (2 mks)
- The curved surface of the frustum (3 mks)
- The hemispherical surface (3 Marks)
- The circular base. (2 mks)
- A similar solid has a total surface area of 81.51cm2. Determine the radius of its base. (2 mks)
- Find the area of
MARKING SCHEME
- Numerator
7/4 x 7/3=49/12
7/5 x 12/49=12/35
3/5 x 12/5= (21-12)/35
= 9/35
Denominator
5/8 x 2/3 = 5/12
10/7 - 5/12 = (120-35)/84
=85/84
Num/Den
=9/35 x 7/5 = 9/25
12/7 x 85/84=5/7 - 118 yens = ksh. 76
∴2,950,000 yens = 2,950,000/118 x 76
=ksh. 1,900,000
The duty paid 20/100 x 1,900,000
=Ksh. 380,000 - 2 + 40/60 = 2 2/3 hours
22/3 x 120 = 320 km
320/4 = 80 litres
80x59 = 4720 sh. - 2πrl=1980
2 x 22/7 x 21 x h = 1980
h=1980/132 = 15cm
v = πr2h = 22/7x 212x 15
= 20790/1000
=20.8l - Adjacent = √132 - 52 = 12
Tan (90 – θ) = 12/5 - 2x – 5y – 10 = 0
5y = 2x – 10
Y = 2/5x - 2
M1= 2/5
M2 = -5/2 B1 gradient of L2
-5/2 = (y+2)/(x-5) M1 Equation
2y + 4 = -5x +2s
2y= -5x + 21
Y = 5/2x + 21/2 - x + 80 =180
180-128=52
52n + 100 = 360
52n=260
n=5
n=5+1=6 - (3x+1)(3x-2)=28
9x2 - 6x + 3x -2=28
9x2 - 3x - 30=0
3x2 - x -10=0
3x2 - 6x + 5x - 10=0
3x(x-2) + 5(x-2)=0
3x+5=0 or x-2=0
x= -5/3, x=2
so x =2
length= 3(2) + 1
=7cm - (2x+y)(2x-y)
3y2 - 7xy + 2x2
3y2 - 6xy - xy + 2x2
3y(y-2x)-x(y-2x)
(3y-x)(y-2x)
so
(2x+y)(2x-y)
(3y-x)(y-2x)
(2x-y)(y-2x)
(x-3y)(2x-y)
= y-2x
x-3y - AB/XY= 12/4 = 3
LSF= 3:1
ASF= 9:1
36 x 1/8
45cm3 -
-
- h= 4.2 ± 0.1 cm
A= ½ x 4 x 4.2
=8.4cm2
-
-
Internal dimensions
Length = 40cm
Width = 20cm
Height = 15cm
Volume of container= 40 x 20 x 15 = 12000cm3
8 liters = 8000cm3
Unoccupied volume = 4000
h 4000/8000 = 5cm
ALT2
40 x 20h = 8000
H=10
change = 15 – 10 = 5cm
Alt 3
40 X 20 (H – 0.5) = 8000
H= 10.5
15.5 – 10.5 = 5cm -
- Centre of rotation=(4, -2)
Angle of rotation = +90º
- 2x – 2 ≤3x+1
-2 – 1 ≤3x-2x
-3 ≤x
3x + 1 < x + 11
2x < 10
X<5
-3 ≤x<5
Integral values -3,-2, -1, 0, 1,2,3,4
12/sin30º =QR/sin70º
QR =12 sin70º/sin30º =22.55cm A1 answer for QR
Area = ½ x 12 x 22.55 x sin 80º
= 133.2 to 4 s.f- Let the number = xy
X+y = 13 y = 13 – x
(10x + y) – (10y + x) = 9
9x – 9y = 9
x-y = 1
x-1 = y
x-1 = 13- x
2x = 14
X=7
Y=13-7
=6cm A1
Original number = 76 -
- y-3 = -1
x--1 2
2(y-3) = -1(x+1)
2y-6 = -x-1
2y= -x+5 - Gradient of L2
5--2 = 4
3-1
y--3 = 4
x-1
y+3 = 4x -4
y = 4x -7
4x - y -7 =0 - Gradient = -1/4
(0, 1.5), (x,y)
y- 1.5 = -1
x -0 4
4y-6 = -x
4y= -x+6 - y=4x-7
4y= -x+6
4(4x-7) = -x+6
16x-28= -x+6
17x=34
x=2
y= 4(2) -7
y=1
- y-3 = -1
-
- a = (v-u)/t
2.75 =(22-0)/t
t=22/2.75
= 8 sec - Distance = ½ x 8 x 22 = 88m
- 847 = ½ ( 40+t) + 32) x 22
847 = ½ (72 +t) x 22
1694 = (72+t) 22
1694/22 = 72 + t
77=72+t
T = 5 sec
T = 40 +t = 40+5 = 45 sec. - a = (v-u)/t = (0-22)/5 = -4.4m/s2
- a = (v-u)/t
-
- PT = PQ + QT = -b + a
- Qx = QP + PX
= b+k(-b+a)
=b-kb + ka
=(1-k)b + ka - QS= QR + RS
= 3a + 2b - QX= t=(3a + 2b)
= (1-k) b + ka
= 3ta + 2tb
k=3t, 1-k=2t
1-3t=2t
5t=1
t=1/5
k=3 x 1/5
=3/5 - PX = 3/5PT
PX:PT = 3:5
PX:XT=3:2
- PT = PQ + QT = -b + a
-
A’(0,10)
B’(2,6) 3
C’(2,10)
A”(10,2)
B”(6,2) 3
C”(10,2)
ΔABC =2 -
- 8.5 x 10 = 85km ± 1
046º ± 1 - 8.3 x 10 = 83km ± 1
247º ± 1 - 123º
- 8.5 x 10 = 85km ± 1
-
-
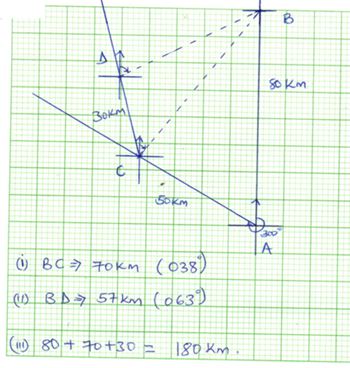
- distance BC = 6.9cm = 6.9 x 10 = 69km
Bearing of B from C = 0.35 -^+ 1 - Distance BD = 5.7 x 10 = 57km
Bearing of B and D = 063 - distance = 80km + 30km + 50km + 57km = 217km
- distance BC = 6.9cm = 6.9 x 10 = 69km
-
-
- 16200/x
- 16200/(x+3)
- 16200/x - 60 = 16200/(x+3)
16200 (x +3) – 60x (x+3) = 16200x
16200x + 48600 – 60x2 – 180x = 16200 x
60x2 +180x – 48600 = 0
X2+3x – 810 = 0
(x+30) (x – 27) = 0
X = -30 or 27
No. of calculators = 27 - initial cost = 16200/27 = 600
After discount = 16200/30
= 540 B1 – Both 600 and 540 seen
% discount =(600-540)/600 x 100%
= 10%
-
-
-
- A= 22/7 x 3.5 x 3.5
=38.5 - 4.2 = 8+x
3.5 x
4.2x = 28 + 3.5x
0.7x=28
x=40
22/7 x 4.2 x 48 - 22/7 x 3.5 x 40
= 633.6 - 440= 193.6 - 2 x 22/7 x 4.2 x 4.2
= 776.16
- A= 22/7 x 3.5 x 3.5
- T. S. A = 776.16 + 193.6 + 38.5 = 1008.26
A.S.F = 81.51 : 1008.26
1: 12.36977
L.S.F = 1.3517
3.517 x 3.5/1
r= 12.31
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Meru Central Cluster Exam 2020.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students