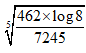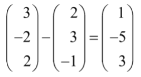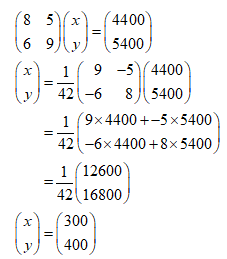Instructions to candidates
- The paper contains TWO Sections: Section I and Section II.
- Answer ALL the questions in Section I and only five questions from Section II.
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
- Answer all the questions in English.
SECTION I (50 marks)
Answer all questions in this section in the spaces provided
-
- Evaluate 825 × 4 + 144 ÷ of (−36 + 30) (2 marks)
- Write the total value of the digit in the thousands place of the results obtained in (a) above (1 mark)
- Given the inequalities 2x − 3 ≤ 4x + 7 < x + 13 solve the inequalities and represent the solution on a number line. (3 marks)
- Simplify completely (3 marks)
8x² − 2
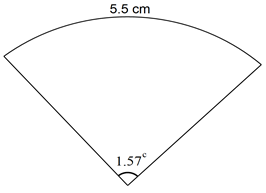
2x3 −7x2 + 3x - The figure below shows a sector of a circle centre O.
Determine- The radius OA of the circle (2 marks)
- The perimeter of the sector (2 marks)
- Solve for in the equation (3 marks)
(1/27)x ÷ 81 = 3√729 - Christmas bulbs made of different colours are set to light after 8 seconds, 10 seconds and 14 seconds. How many times will they light simultaneously in one hour if they start together? (3 marks)
- A bus left Nairobi at 7.00 a.m and travelled towards Mombasa at an average speed of 80 km/hr. At 8.00 a.m, a car left Mombasa towards Nairobi at an average speed of 120 km /hr. If the distance between Mombasa and Nairobi is 500 km , calculate the time of the day the two vehicles met (4 marks)
- →
The position vectors of point P and Q are 2i + 3j − k and 3i − 2j + 2k respectively. Find the magnitude of PQ to 4 significant figure. (3 marks) - Solve the equation 2 Cos 3x = √3 for 0° ≤ x ≤ 180° (2 marks)
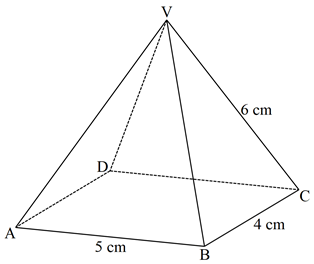
- The diagram below represents a right rectangular based pyramid of 5 cm by 4 cm. The slant edge of the pyramid is 6 cm. Draw and label the net of the pyramid. (3 marks)
- Two cylindrical containers are similar. The larger one has an internal cross-sectional area of 45 cm2 and can hold 0.945 litres of liquid when full. The smaller container has internal cross-sectional area of 20 cm2. Calculate the capacity of the smaller container. (3 marks)
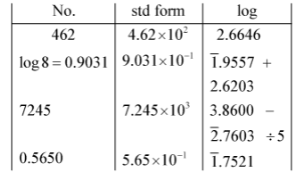
- Use logarithms correct to 4 decimal places to evaluate (3 marks)
- One interior angle of a polygon is a right angle and each of the other interior angles is 126°. Calculate the number of sides of the polygon. (3 marks)
- Use the exchange rates below to answer this question.
Buying Selling
1 US dollar 103.00 103.20
1 UK £ 125.30 125.95
A tourist arrived in Kenya from Britain with 8400 UK Sterling pounds (£). He converted the whole amount to Kenya shillings. While in Kenya, he spent ¾ of this money and changed the balance to US dollars. Calculate the amount of money, to the nearest US dollars, that he received. (3 marks) - Joan and Gloria working together can do a piece of work in 12 hours. Joan, working alone takes 10 hours longer than Gloria. How many hours does it take Gloria to do the work alone? (3 marks)
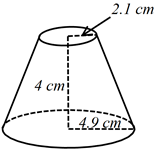
- The diagram below represents a solid of a conical frustrum. (use π = 22/7)
Calculate the volume of the solid (4 marks)
SECTION II (50 marks)
Answer any five questions in this section in spaces provided
- Given that a line passes through the points and , find;
- The equation of line L1 in the form y = mx + c (2 marks)
- The equation of a line L2 , which is perpendicular bisector of line L1. Leave your answer in the form ax + by = c, where a, b and c are integers. (3 marks)
- Given that another line L3 is parallel to L2 and passes through point (−3, −5) and intersects line L1 at point .
(2 marks) - The coordinates of the point of intersection of lines L1 and L3 (3 marks)
-
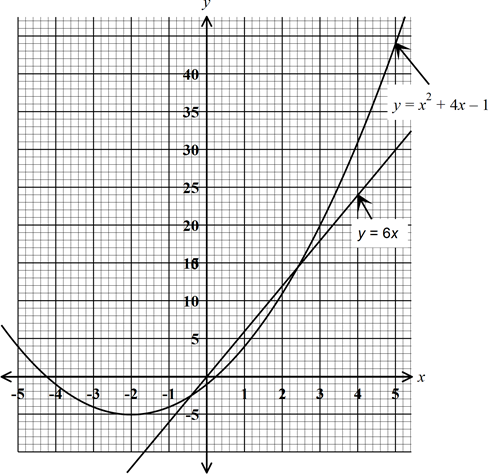
- Draw the graph of the function y = −x2 + 4x − 1 for −1 ≤ x ≤ 5. (5 marks)
x −1 0 1 2 3 4 5 y - Use the graph above to solve the equations:
- x3 + 4x − 1 = 0 (2 marks)
- x2 − 2x − 1 = 0(3 marks)
- Draw the graph of the function y = −x2 + 4x − 1 for −1 ≤ x ≤ 5. (5 marks)
-
- Given that P =
, find (2 marks)
- Matawi bought 8 T-shirts and 5 pairs of shorts at a total cost of ksh. 4400. Had he bought 6 T-shirts and 9 pairs of shorts, he would have spent ksh. 1000 more.
- Form two equations to represent the above information (2 marks)
- Use the matrix method to determine the cost of a T-shirt and a pair of shorts (3 marks)
- Three months later the price of a pair of shorts went up. Matawi bought 5 T-shirts and 5 pairs of shorts at a total cost of ksh. 3650. Find the percentage increase in the price of a pair of shorts. (3 marks)
- Given that P =
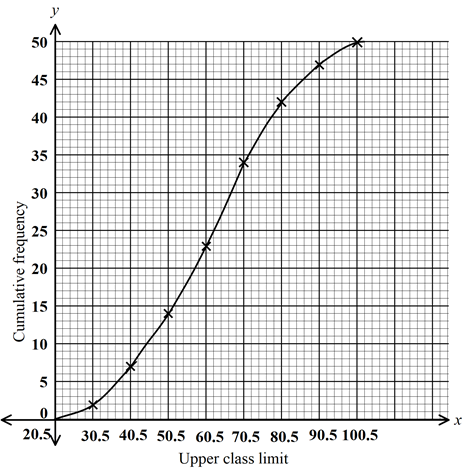
- The marks of 50 students in a Mathematics test were taken from a form 3 class and recorded in the table below.
Marks (%) 21-30 31-40 41-50 51-60 61-70 71-80 81-90 91-100 Frequency (ƒ) 2 5 7 9 11 8 5 3 - On the grid provided, draw a cumulative frequency curve of the data above. Use a scale of 1 cm to represent 5 students on the vertical scale and 1 cm to represent 10 marks on the horizontal scale. (3 marks)
- From your curve in (a) above;
- Estimate the median mark. (1 mark)
- Determine the interquartile deviation. (2 marks)
- Determine the 10th and 90th percentile range. (2 marks)
- It is given that the students who scored over 45 marks pass the test. Use your graph in (a) above to estimate the percentage of students that pass the test. (2 marks)
-
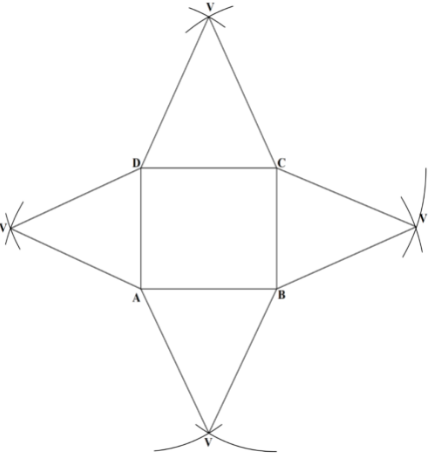
- On the Cartesian plane below , draw triangle ABC with vertices A(0, −1), B(4,3) and C (2,2) (1 mark)
- Draw triangle A'B'C', the image of ABC under a transformation defined by the translation vector T =
. Write down the coordinates of A'B'C'. (3 marks)
- A''B''C'' is the image of A'B'C' under an enlargement, scale factor −2, centre (3,1). On the same plane draw A''B''C'' and write down its coordinates. (4 marks)
- Draw A'''B'''C''', the image of A''B''C'', under reflection in the line x = 0 . (2 marks)
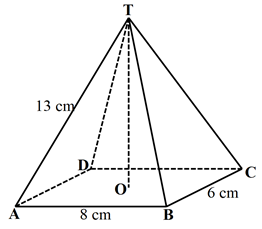
- The figure below is of a right pyramid on a rectangle base of 8cm by 6cm and Its slant edge .
TA = TB = TC = TD = 13cm
Calculate:- The length of AC (1 mark)
- The height of the pyramid (1 mark)
- The angle between TAB and plane TCD. (2 marks)
- The angle between TAB and plane TBC. (4 marks)
- The volume of the pyramid. (2 marks)
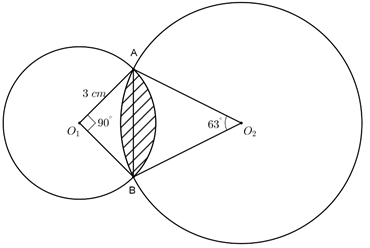
- The figure below shows two circles, centres O1 and O2 intersecting at points A and B. The radius of the circle centre is O1 3cm. Further, and ∠ AO1B = 90° and ∠ AO2B = 63°
Calculate correct to four significant figures- The length of the common chord AB. (2 marks)
- The radius of the circle center O2 (2 marks)
- Hence, calculate the area of the shaded region. (use π = 22/7) (6 marks)
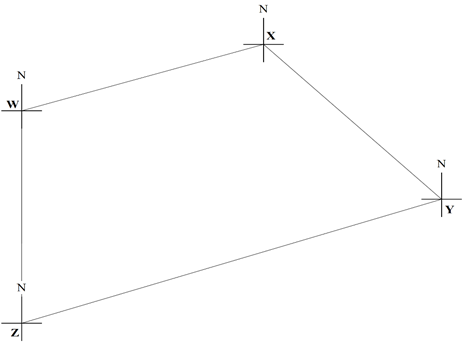
- During a surveying exercise to establish a housing estate a surveyor marked out four points W,X,Y and Z to represent an area to be left out for a shopping complex and social amenities. Point X is 240m on a bearing of 073° from point W. Point Y lies on a bearing of 145° at a distance of 300m from X. Z is directly south of W a distance of 320m.
- Draw a scale diagram to represent the relative positions of the area under survey
Scale 1cm represents 40m. (4 marks) - Using the scale diagram in (a) above, determine
- The distance and bearing of point Z from Y. (2 marks)
- The bearing of point X from point Z. (1 mark)
- A road is to be constructed directly South of X to meet another road from Y westwards at point P. Find the area enclosed by triangle PXY in hectares. (3 marks)
- Draw a scale diagram to represent the relative positions of the area under survey

MARKING SCHEME
-
- 825 × 4 + 144 ÷ 4 of −6
825 × 4 + 144 ÷ −24
3300 + −6
=3294 - 3 × 1000 = 3,000
- 825 × 4 + 144 ÷ 4 of −6
- 2x − 3 ≤ 4x + 7
−3−7 ≤ 4x − 2x
−10 ≤ 2x
−5 ≤ x
4x + 7 < x + 13
4x − x < 13 − 7
3x < 6
x < 2
−5 ≤ x < 2 - 8x2 − 2
2(4x2 − 1)
2(2x −1)(2x +1)
x(2x2 − 7x + 3)
2x2 − 6x − x + 3
2x (x −3) −1(x −3)
x(2x −1) (x −3)
2(2x −1)(2x +1)
x(2x −1) (x −3)
2(2x + 1)
x(x − 3)
4x + 2
x2 − 3x\ -
- 1.57 × r = 5.5
r = 5.5 ÷ 1.57
r =] 3.5032 cm - = (3.5032 + 3.5032 + 5.5) cm
= 12.5064 cm
- 1.57 × r = 5.5
- 3−3x ÷ 34 = 32
−3x − 4 = 2
−3x = 6
x = −2 - 8 = 23
10 = 2 × 5
14 = 2 × 7
L.C.M = 23 × 5 × 7 = 280 seconds
3600 ÷ 280 = 12.527
= 12 times - Distance covered by bus by 8.00am
1hr × 80 km/h = 80km
Distance covered by both vehicles before meeting
500 − 80 = 420km
Relative speed 80 + 120 = 200km
Time taken to meet 420/200 = 2hrs 6 mins
Time the two met 8:00am + 2hrs 6 mins = 10.06 am -
√(12 + (−5)2 + 32) = √35
= 5.916 units - cos3x = √3/2
3x = 30°, 330° ,390°, 690°
x = 10°,110°,130° -
- A.S.F = 20/45 = 4/9
L.S.F = 2/3
V.S.F = (2/3)3 = 8/27
27/8 × 0.945 = 0.28 litres -
- 90 + 126(n − 1) = 180(n −2)
90 + 126n − 126 = 180n −360
90 + 360 − 126 = 180n −126n
324 = 54n
n = 6 - 8400 × 125.3 = ksh 1,052,520
balance = ¼ × 1,052,520 = Ksh 263,130
amount of us dollars recieved
263,130 = 2550
103.2 - 1/12 = 1/x + 1/x+10
1 = 2x + 10
12 x2 + 10x
24x + 120 = x2 + 10x
x2 − 14x − 120 = 0
x2 − 20x + 6x − 120 = 0
x(x −20) + 6(x − 20) = 0
(x + 6) (x−20) = 0
x = 20
Gloria takes 20hrs - h = 2.1
h+4 4.9
h = 2.1h + 8.4
h = 3
Volume = ( 1/3 × 22/7 × 4.92 × 7) − (1/3 × 22/7 × 2.12 × 3)
= 176.07333 − 13.86
=162.2133 -
- gradient = −1−5 = −3
3−−1 2
equation = y − 5 = −3
x + 1 2
2(y − 5) = −3(x + 1)
2y−10 = −3x −3
2y = −3x + 7 - gradient of line 2 = 2/3
mid point of line L1 =(1,2)
equation = y − 2 = 2
x −1 3
3(y − 2) = 2(x −1)
3y − 6 = 2x − 2
3y = 2x + 4 - gradient of L3 = 2/3
equation = y + 5 = 2
x + 3 3
3(y+5) = 2(x +3)
3y + 15 = 2x + 6
3y = 2x − 9 - 2(3y = 2x − 9)
3(2y = −3x + 7)
6y = 4x − 18}−
6y = −9x + 21}
0 = 13x −39
x = 3
3y = 2(3) − 9
y = −1
(3,−1)
- gradient = −1−5 = −3
-
-
x −1 0 1 2 3 4 5 y −4 −1 4 11 20 31 44 -
- x = − 4.2
x = 0.2 - y = x2 + 4x −1}
0 = x2 − 2x − 1} −
y = 6x
x = −0.4
x = 2.4
- x = − 4.2
-
-
-
det = (8 × 9) − (6 × 5) = 42
P−1 = -
- 8x + 5y = 4400
6x + 9y = 5400 -
- 8x + 5y = 4400
- 5 × 300 + 5y = 3650
5y = 3650 − 1500
y = 430
% increase = 30/400 × 100% = 7.5%
-
-
-
U.C.L 30.5 40.5 50.5 60.5 70.5 80.5 90.5 100.5 C.F 2 7 14 23 34 42 47 50 -
- Q2 = 62.5 marks
- Q3 = 74.5, Q1 = 48.5
Q3 − Q1 = 74.5 − 48.5
= 26
Q₃ − Q₁ = 26 = 13
2 2 - 10th percentile = 36.5 marks and 90th percentile = 86.5 marks
Range = 86.5 − 36.5 = 50 marks
- students who score 45 marks and below 11.
45 marks and above 50 − 11 = 39 students.
∴ % scoring over 45 marks = 39/50 × 100% = 78%
-
-
-
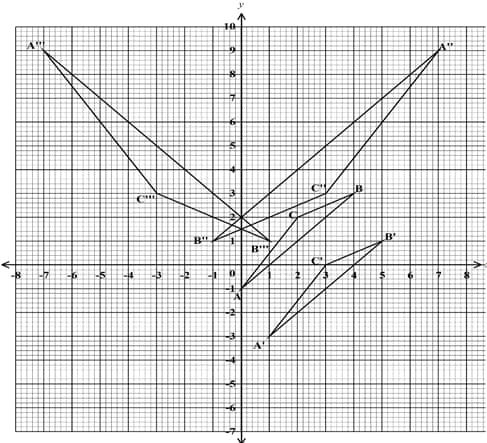
- A'(1, −3), B'(5,1), C'(3,0)
- A''(7,9). B''(−1, 1), C''(3,3)
-
-
- = √(82 + 62) = 10cm
- =√(132 − 52) = 12cm
- tan θ = 3/12
θ = 14.04° × 2 = 28.08° - √(132 − 42) = √153
√(132 − 32) = √160
√(42 + 32) = 5
52 = (√153)2 + (√160)2 − 2 × √153 × √160 cos x
25 = 153 + 160 − 312.92 cos x
25 − 313 = − 312.92 cos x
− 288 = − 312.92 cos x
cos x = 0.9204
x = 23.02° - 1/3 × 8 × 6 × 12 = 162cm3
-
- AB = √(32 + 32)
= √26
= 4.243 cm - 1.121 = sin 31.5
x
x = 1.121 = 4.060cm
sin 31.5 -
(90/360 × 22/7 × 32) − (½ × 3 × 3) = 2.571
(63/360 × 22/7 × 4.062) − (½ × 4.062 sin 63°) = 1.723
shaded area
2.571 + 1.723 = 4.294
- AB = √(32 + 32)
-
-
-
- 420m, 248° ±1°
- 030° ±1°
- 2.083ha
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Pavement Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students